5.2.2.2. Dahlinov algoritam

E.B. Dahlin je krajem 60-ih godina (E.B. Dahlin, Designing and Tuning Digital Controllers, Inst. And Control Systems, June 1968) objavio rad o projektiranju diskretnog regulatora u diskretnom području. Njegov je postupak samo specijalni slučaj metode postavljanja polova i nula regulatora uz definiranje modela željenog ponašanja zatvorenog regulacijskog sustava. Specijalni slučaj je u tome što je regulacijska shema standardna sa samo jednim regulatorom u serijskoj grani iza sumatora. Prikazuje je slika 5.2.19.

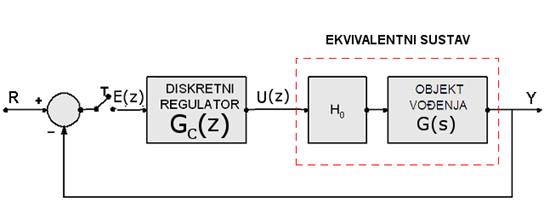
Slika 5.2.19. Regulacijska shema projektiranja regulatora po Dahlinovom postupku

Označimo li s G_E(z) ekvivalentnu impulsnu prijenosnu funkciju kontinuiranog dijela sustava jednadžba vođenog sustava u z području glasi:

    (5.2.18)

Riješimo li ovu jednadžbu po nepoznatoj impulsnoj prijenosnoj funkciji regulatora dobiti ćemo:

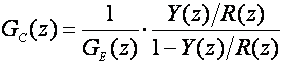    (5.2.19)

Ovo je polazna jednadžba za proračun regulatora. Da bismo je primijenili treba nam:

a)  ekvivalentna impulsna prijenosna funkcija kontinuiranog dijela sustava G_E(z)

b)  željena impulsna prijenosna funkcija vođenog sustava Y(z)/R(z).

Željena impulsna prijenosna funkcija definira se u s području kao prijenosna funkcija prvog reda s kašnjenjem:

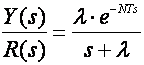           (5.2.20)

Kašnjenje je cjelobrojni višekratnik perioda uzorkovanja.

U z području Y(z)/R(z) računamo kao ekvivalentnu impulsnu prijenosnu funkciju zatvorenog regulacijskog sustava:

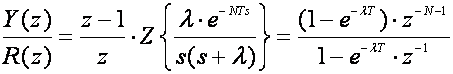           (5.2.21)

Uvrstimo li ovaj izraz u jednadžbu regulatora (5.2.19) dobijemo:

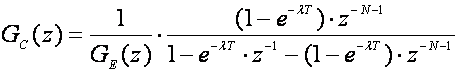           (5.2.22)

Proračun konkretnog regulatora je vezan s ekvivalentnom impulsnom funkcijom sustava koji se vodi. Dahlin je razmatrao dvije situacije.