Vođeni sustav aproksimiramo prijenosnom funkcijom prvog reda s kašnjenjem
U poglavlju o eksperimentalnom podešavanju PID regulatora postupkom reakcijske krivulje kazali smo da je prijenosna funkcija prvog reda s kašnjenjem model kojim možemo aproksimirati veliki broj realnih sustava. Karakteriziraju je tri parametra – pojačanje, vremenska konstanta sustava i kašnjenje:
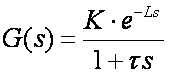 (5.2.23)
(5.2.23)
Da bi sustav vođenja bio fizički ostvariv konstanta N kod kašnjenja željenog modela treba biti najveća cjelobrojna vrijednost stvarnog kašnjenja sustava L.
Ekvivalentna impulsna prijenosna funkcija vođenog sustava je
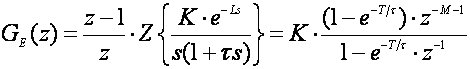 (5.2.24)
(5.2.24)
gdje je M cjelobrojni višekratnik omjera L/T.
Napomena: Zaokruživši kašnjenje kontinuiranog sustava na MT unosimo pogrešku koju bismo mogli ispraviti korištenjem modificirane Z - transformacije. U tom bi slučaju ekvivalentna impulsna prijenosna funkcija željenog sustava glasila
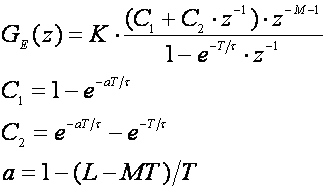 (5.2.25)
(5.2.25)
i cijela kasnija sinteza bi se temeljila na njoj. Ne zaboravimo da je M cjelobrojni višekratnik omjera L/T. Međutim ukoliko je T dovoljno mali i aproksimacija (5.2.24) može dati zadovoljavajuće rezultate.
Uvrstimo li (5.2.24) u (5.2.22) dobijemo željenu impulsnu prijenosnu funkciju regulatora:
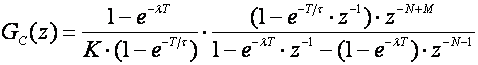 (5.2.26)
(5.2.26)
a uvrstimo li (5.2.25) u (5.2.22) dobijemo
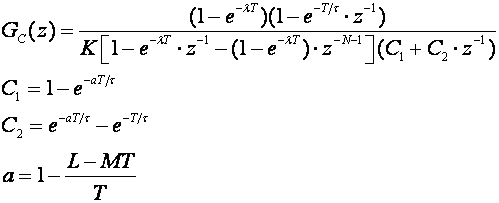 (5.2.27)
(5.2.27)
Specijalni je slučaj kada i željeni model ponašanja zatvorenog sustava i vođeni sustav nemaju kašnjenje N=M=0. Jednadžba regulatora tada glasi:
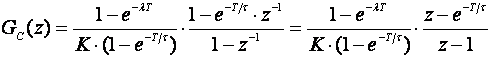 (5.2.28)
(5.2.28)
a kako je T sigurno manji od τ, nula regulatora će se nalaziti između točke z=1 i točke z=0. Prisjetimo li se poglavlja o regulatorima s faznim prethođenjem i kašnjenjem, u ovom slučaju je očito da se radi o regulatoru s faznim kašnjenjem, odnosno o regulatoru PI tipa.
Napomena: Dopustimo sebi malu digresiju i vratimo se u kontinuirano područje. I u njemu vrijedi izraz za proračun regulatora oblika:
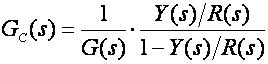 (5.2.29)
(5.2.29)
Neka željeno ponašanje sustava opisuje prijenosna funkcija
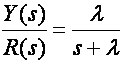 (5.2.30)
(5.2.30)
i neka je sustav koji se vodi također prvog reda
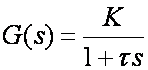 (5.2.31)
(5.2.31)
Regulator će imati oblik
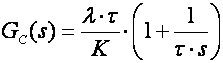 (5.2.32)
(5.2.32)
Očito je da se i ovdje radi o regulatoru PI tipa.
Ilustrirajmo postupak primjerom koji su opisali Chiu i suradnici 1973. godine u članku kojim objašnjavaju Dahlinov postupak (K-C. Chiu, A.B. Corripio, C.L. Smith, Digital Control Algorithms, Part1. Dahlin Algorithm, Inst. & Control Systems, pp. 57-59, Oct. 1973):
Primjer:
Slika 5.2.20 prikazuje sustav regulacije temperature egzotermičkog reaktora hlađenog vodom. Upravljana varijabla je temperatura u reaktoru, a upravljačka varijabla je protok rashladne vode. Pri nekoj stacionarnoj vrijednosti protoka u reaktoru se održava određena temperatura.
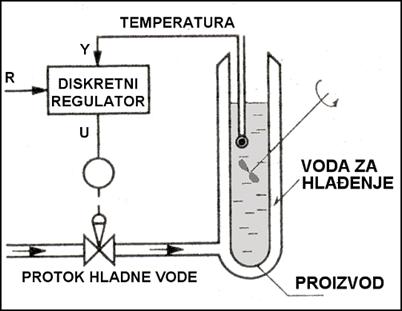
Slika 5.2.20. Egzotermički reaktor hlađen vodom
Promjeni li se protok skokovito i snimi se reakcijska krivulja, sustav hlađenja koji kao izlaznu varijablu ima temperaturu, a kao ulaznu varijablu protok hladne vode može se prikazati prijenosnom funkcijom prvog reda s kašnjenjem:
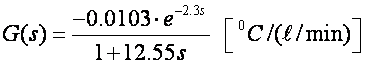
Napomena: Pojačanje je negativno zato što povećanje protoka smanjuje temperaturu. Jedinica vremena je u originalnom primjeru bila minuta pa ćemo je i ovdje zadržati i u odnosu na nju definirati period uzorkovanja.
Pogledajmo dva slučaja za λ=1 i λ=0.5. Neka je T=1 [minuta], a iz modela procesa očitavamo L=2.3, K=-0.0103 i τ=12.55. Period uzimanja uzoraka je usporediv s kašnjenjem procesa pa za proračun regulatora koristimo jednadžbu (5.2.27).
Za λ=1 rezultat je:
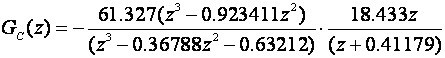
a za λ=0.5:
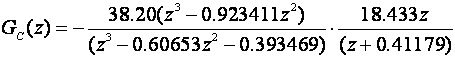
Slika 5.2.21 prikazuje odzive za oba slučaja i situaciju kada se temperatura koja se ustalila na vrijednosti 900C treba smanjiti na 800C u trenutku t=5 minuta. Kako sustav ima kašnjenje, odziv se počinje mijenjati tek nakon 2.3 minute. Prikazan je i upravljački signal za oba slučaja. Njegove vrijednosti su u stvari promjene protoka oko stacionarne vrijednosti kod koje je temperatura u reaktoru bila 900C. U stacionarnom stanju kada se temperatura ustalila na 800C, zahtjev je da se protok u odnosu na vrijednost koju je imao za 900C poveća za 970.87 l/min.
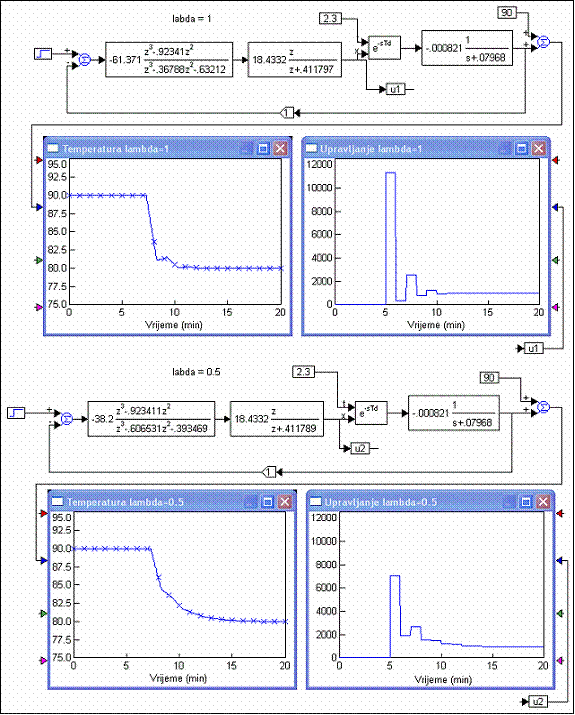
Slika 5.2.21. Rezultati primjene Dahlinovog regulatora za λ=1 i λ=0.5 (sinteza-Dahlin.vsm)
Odziv je (više ili manje) aperiodički, ali je najveći problem u upravljačkom signalu koji u prijelaznom dijelu alternirajući mijenja vrijednosti u velikim skokovima, a i potrebne vrijednosti protoka su velike (u prvom diskretnom trenutku preko 7.000 l/min, a pitanje je da li se to s realnim veličinama cijevi može ostvariti. Više detalja o ovom problemu u sljedećem poglavlju: Treptanje (ili zvonjenje) upravljačkog signala. Na kraju napomenimo još i to da su za manji λ promjene upravljanja su manje, ali je i odziv sporiji.