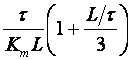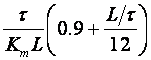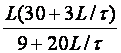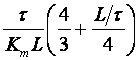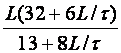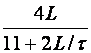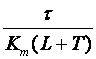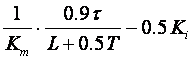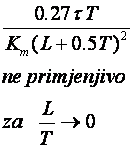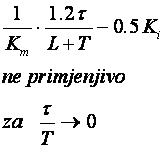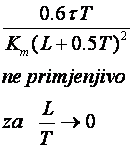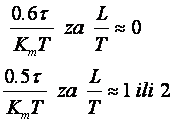Digitalno vođenje on-line (FESB, Split)

Podešavanje parametara PID regulatora postupkom reakcijske krivulje

Cilj: Naučiti i drugi postupak eksperimentalnog podešavanja parametara PID regulatora koji zahtjeva testiranje samog sustava koji se vodi.

Originalni postupak također su dali Ziegler i Nichols kao postupak primjenjiv u slučajevima kada se može snimiti odziv samog sustava koji se vodi na skokovitu pobudu, pa se često naziva postupak s otvorenom petljom. U engleskom govornom području susreće se pod nazivom Reaction Curve Method ili Step-response Method.

Zeigler i Nichols su je primjenjivali i na:

a) sustave s izjednačenjem, koje nazivamo i samoregulacijski sustavi, ne-integracijski sustavi, sustavi 0-te vrsti (nemaju polova u ishodištu s ravnine) i na

b) sustave bez izjednačenja, koje nazivamo i ne-samoregulacijski sustavi, integracijski sustavi ili sustavi ne-nulte vrsti sustave (imaju polova u ishodištu s ravnine),

dok su se Cohen i Coon, čiji tablice navodimo kasnije, ograničili samo na sustave s izjednačenjem.

U svim slučajevima ukoliko se radi o sustavu s izjednačenjem, vođeni dio sustava se aproksimira prijenosnom funkcijom prvog reda s kašnjenjem:

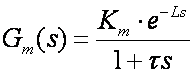(5.1.55)

Postupak podešavanja se sastoji u snimanju odziva otvorenog sustava na skokovitu pobudu, određivanjem vrijednosti K_m, L i τ, te proračun parametara PID regulatora prema Zeigler-Nicholsovoj tablici, ovisno o kojem se tipu regulatora radi. Primjer odziva s označenim parametrima prikazuje slika 5.1.27, a parametri su dani u tablici 5.5. Tablica je primjenjiva i na sustave s izjednačenjem i na sustave bez izjednačenja.

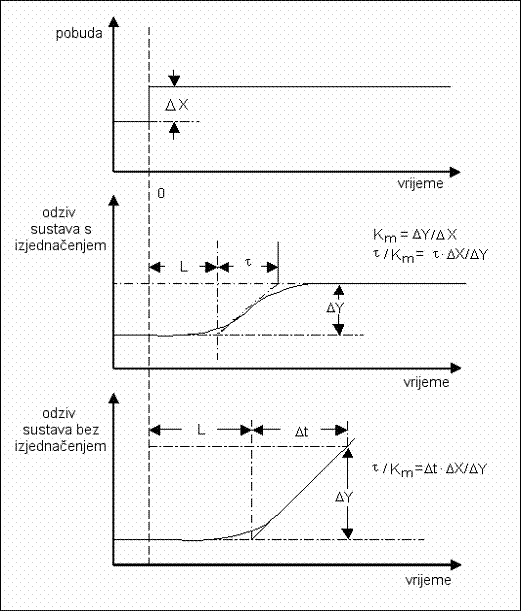
Slika 5.1.27. Definicija parametara na odzivu otvorenog sustava na jediničnu skokovitu pobudu

	K	T_i	T_d
P	τ/ K_m L	-	-
PI	0.9 τ/ K_m L	3.33 L	-
PID	1.2 τ/ K_m L	2 L	0.5 L

Tablica 5.5. Podešavanje parametara kontinuiranog PID regulatora Zeigler - Nicholsovim postupkom reakcijske krivulje (eng. Reaction Curve Method)

Neki od autora dopuštaju da odziv otvorenog sustava bude i oscilatorno prigušen te da se parametri K_m, L i τ odrede na isti način.

Pogledajmo primjer prijenosne funkcije drugog reda na koju nismo mogli primijeniti postupak stabilnosne granice.

Primjer:

Za sustav prijenosne funkcije 1.68/(.231s²+1.3s+1) odredi optimalne parametre podešavanja PID regulatora metodom reakcijske krivulje.

Slika 5.1.28 pokazuje odziv sustava na jedinični skok.

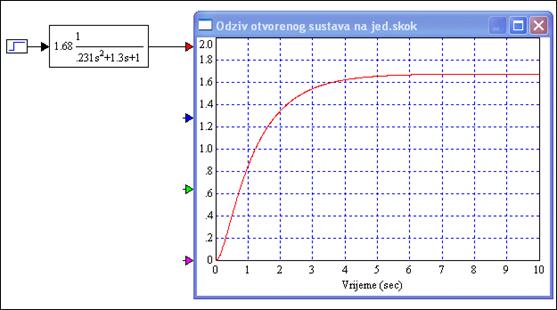
Slika 5.1.28. Odziv otvorenog sustava na jedinični skok

Koristeći opciju 'Read Coordinates...' na odzivu smo izmjerili K_m = 1.68, τ = 1.245 i L=0.15, pa su Zeigler-Nicholsove vrijednosti parametara PID regulatora:

K = 1.2 τ/ K_m L = 5.928

T_i = 2 L = 0.3

T_d = 0.5 L = 0.075

Slika 5.1.29 prikazuje odziv sustava vođenog PID regulatorom s ovako podešenim parametrima

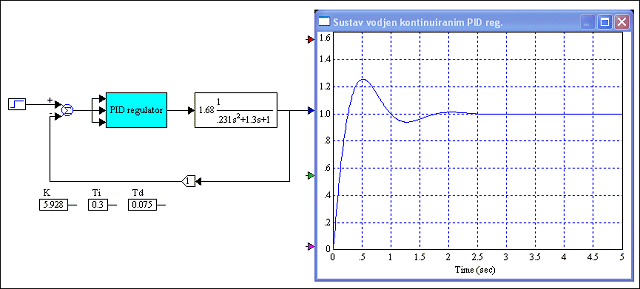
Slika 5.1.29. Sustav vođen kontinuiranim PID regulatorom kojem su parametri određeni metodom reakcijske krivulje (PID-podesavanje_parametara-reakcijska_krivulja.vsm)

I drugi su autori predlagali svoje tablice podešavanja PID regulatora i svaki je imao određeno opravdanje zašto predlaže baš takve vrijednosti. Kao primjer navodimo način proračuna parametara po postupku Chien – Hranes – Resewicha. Oni prave razliku između PID regulatora u zadacima stabilizacije i u zadacima slijednog vođenja. Drugi je primjer isto tako klasični postupak Cohen – Coona i postupci temeljeni na minimizaciji integralnih kriterija kvalitete odziva.

Stabilizacijsko vođenje

	K	T_i	T_d
P	0.7 τ/ K_m L	-	-
PI	0.7 τ/ K_m L	2.3 L	-
PID	1.2 τ/ K_m L	2 L	0.42 L

Slijedno vođenje

	K	T_i	T_d
P	0.7 τ/ K_m L	-	-
PI	0.6 τ/ K_m L	τ	-
PID	0.95 τ/ K_m L	1.36 τ	0.47 L

Tablica 5.6. Podešavanje parametara kontinuiranog PID regulatora prema Chien – Hranes – Resewichu (K.L. Chien, J.A. Hrones, I.B. Reswich, On the Automatic Control of Generalized Passive Systems, Transaction ASME, 74, 1952)

Snimljeni odziv treba biti granično aperiodički a parametri su određeni uz pretpostavku da nadvišenje ne pređe 20%. Razlika je u podešavanju parametara između stabilizacijskog i slijednog vođenja

Tablica 5.7 prenosi još jedan od klasičnih načina podešavanja PID regulatora po Cohen-Coonu uvedenog 1953. godine (G.H. Cohen, G.A. Coon, Theoretical consideration of retarded control, Trans.ASME, Vol.75, pp. 827-834, 1953). Proračun parametara regulatora vezan je s padanjem amplituda prigušenih oscilacija. U odzivu vođenog sustava drugo nadvišenje bi trebalo biti 25% prvog nadvišenja (omjer druge i prve amplitde oscilacija u engleskoj literaturi se naziva subsidence ratio i on u slučaju Cohen-Coonovog podešavanja iznosi 1/4 ).

	K	T_i	T_d
P		-	-
PI			-
PID

Tablica 5.7. Podešavanje parametara kontinuiranog PID regulatora prema Cohen-Coonu.

Primjer:

Za prethodni primjer ostali načini podešavanja uz K_m = 1.68, τ = 1.245 i L=0.15 daju sljedeće rezultate:

Stabilizacijski Chien – Hranes – Resewich

K = 5.928

T_i = 0.3

T_d = 0.63

Slijedni Chien – Hranes – Resewich

K = 4.693

T_i = 1.6932

T_d = 0.0705

Cohen-Coon

K = 6.736

T_i = 0.3515

T_d = 0.05337

Slika 5.1.30 prikazuje odzive sustava vođenog kontinuiranim PID regulatorom za različite načine podešavanja parametara PID regulatora.

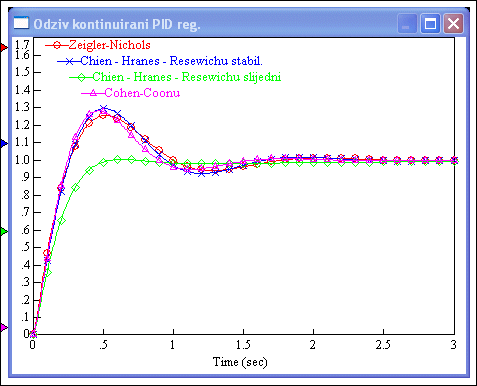
Slika 5.1.30. Sustav vođen kontinuiranim PID regulatorom kojem su parametri određeni metodom reakcijske krivulje na sva četiri opisana načina (PID-podesavanje_parametara-reakcijska_usporedba.vsm)

Svi su odzivi vrlo slični osim za slijedno Chien – Hranes – Resewichovo podešavanje, kada je odziv nešto sporiji, ali je zato bez prebačaja što je poželjnije u slijednom režimu rada sustava vođenja.

Y. Takahashi sa suradnicima (Y. Takahashi CM.J. Rabins, D.M. Auslander, Control and Dynamic Systems, Addison Wesley, 1970) napravio je modifikaciju originalnog Zeigler – Nicholsovog postupka primjenjivu za digitalno vođenje uzevši u obzir i period uzorkovanja. Vrijednosti njegovih parametara za postupak reakcijske krivulje dane su u tablici 5.8 (Napomena: Pazite parametri regulatora se i ovdje navode za idealno paralelnu formu PID regulatora).

	K	K_i =K/T_i	K_d =KT_d
P		-	-
PI			-
PID	_i

Tablica 5.8. Podešavanje parametara diskretnog PID regulatora postupkom reakcijske krivulje (eng. Reaction Curve Method)

Ponovimo prethodni primjer sada za diskretni regulator.

Primjer:

Uz period uzimanja uzoraka T=0.1 i K_m = 1.68, τ = 1.245 i L=0.15 parametri diskretnog PID regulatora po Takahashiu trebali bi biti:

K_i = 1.1116

K = 3.001

K_d = 3.705

Prebacimo to u konstante paralelne realizacije:

K = 3.001

T_i = K/ K_i = 2.6997

T_d = K_d /K= 1.2346

Slika 5.1.31 prikazuje odzive sustava vođenih diskretnim regulatorom (s obje modifikacije, ali bez zasićenja izvršnog uređaja) za vrijednosti parametara proračunate originalnom Ziegler-Nicholsovom metodom za kontinuirane sustave i Takahshievom metodom i uspoređuje ih s odzivom kontinuiranog regulatora. Diskretni regulator za Zeigler-Nicholsovo podešavanje parametara ima čak bolji odziv od kontinuiranog, a zanimljivo je Takahashieva metoda u ovom primjeru daje odziv bez prebačaja.

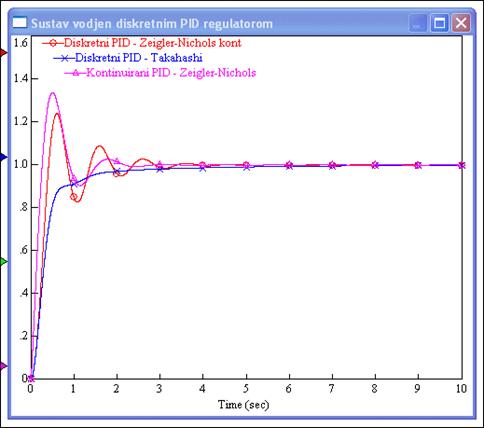
Slika 5.1.31. Usporedba odziva sustava vođenih kontinuiranim i diskretnim regulatorom (s obje modifikacije, ali bez zasićenja izvršnog uređaja) za vrijednosti parametara proračunate metodom reakcijske krivulje originalnom Ziegler-Nicholsovom metodom i Takahshievom metodom (PID-podesavanje_parametara-reak_krivulja_diskretni.vsm)

Napomena: Svi postupci koji se odnose na podešavanje PID regulatora za vođenja sustava s izjednačenjem pretpostavljaju da je odziv sustava aperiodički i da se može aproksimirati prijenosnom funkcijom oblika (5.1.55). Međutim preporuke o podešavanju ponekad se koriste i kao polazne vrijednosti za finija podešavanja i u slučajevima kada je odziv oscilatorno prigušen. K_m je u tom slučaju omjer vrijednosti izlaznog signala na koju će se izlazni signal smiriti i ulaznog skoka. Već smo i napomenuli da se Zeigler - Nicholsove preporuke mogu koristiti i u situacijama kada je sustav bez izjednačenja.

Treći je postupak sličan ovome, ali se parametri regulatora podešavaju sa ciljem minimizacije ITSE integralnog kriterija kvalitete odziva.