5.1.4.4. Regulatori s faznim prethođenjem i kašnjenjem (PD i PI)
U primjeru iz poglavlja o diskretizaciji kontinuiranih regulatora (slika 5.1.6) upotrijebili smo regulator oblika Gc(s) = 10(s+1)/(s+10) za koji smo kazali da je regulator PD tipa koji se unosi s ciljem poboljšavanja dinamičkih svojstava odziva i proširenja stabilnog područja vođenog sustava. Regulator je bio PD tipa zato što mu se nula nalazila bliže ishodištu, pa je derivacijski dio regulatora (brojnik) bio dominantan. U slučaju da se pol nalazio bliže ishodištu regulator bi bio PI tipa, zato što bi njegovim ponašanjem dominirao integracijski dio (nazivnik), a u regulacijski krug ga uključujemo ukoliko želimo utjecati na ponašanje sustava u stacionarnom stanju (pogreške ustaljenog stanja).
Ovakavi tipovi regulatora obično se karakteriziraju svojim faznim doprinosom ukupnoj fazi sustava, pa ovisno o tome da li dominira brojnik ili nazivnik razlikujemo regulatore s faznim prethođenjem (PD tip) i regulatore s faznim kašnjenjem (PI tip). Prijenosna funkcija ova dva tipa regulatora je općenito oblika:
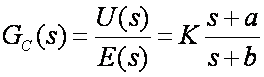(5.1.58)
Ukoliko je a < b radi se o regulatoru s faznim prethođenjem (eng. Phase-Lead Regulator), a ukoliko je a > b o regulatoru s faznim kašnjenjem (eng. Phase-Lag Regulator).
Napomena: Fazno prethođenje ili kašnjenje najbolje se vidi iz GMK – geometrijskog mjesta korijena kao fazni doprinos koji regulator daje zatvorenom regulacijskom sustavu. Faza sustava za bilo koju točku s0 koja pripada GMK određuje se jednadžbom argumenta. Doprinos regulatora je fazni kut vektora povučenog iz nule regulatora do točke s0 minus fazni kut vektora povučenog iz nule regulatora do točke s0. Ukoliko je nula bliže ishodištu njen fazni kut će biti veći, pa će ukupan doprinos biti pozitivan, a ukoliko je pol bliže ishodištu doprinos regulatora će biti negativan. Odatle i naziv regulatoru – regulator s faznim prethođenjem ili kašnjenjem. Slika 5.1.34 prikazuje ove dvije situacije grafički.
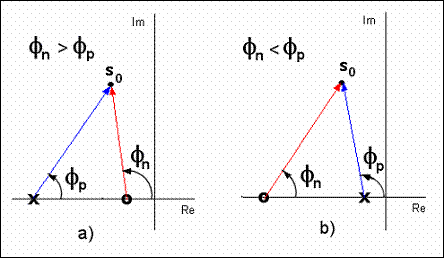
Slika 5.1.34. Doprinos singularnih točaka regulatora a) s faznim prethođenjem i b) s faznim kašnjenjem, fazi zatvorenog regulacijskog sustava
Jednadžba (5.1.58) može se prebaciti u diskretno područje na bilo koji način opisan u poglavlju 5.1 Diskretizacija kontinuiranih regulatora. Pogledajmo primjer Tustinove aproksimacije:
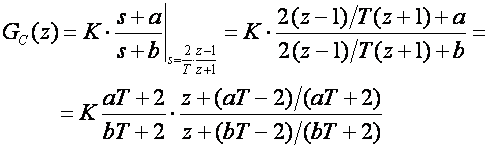(5.1.59)
Opći oblik regulatora u z području je isti kao i u s području. Regulator ima jedan pol i jednu nulu
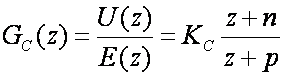(5.1.60)
Tustinova aproksimacija spada u bilinearne transformacije kod kojih se lijeva poluravnina jednoznačno preslikava u jediničnu kružnicu (vidi sliku 5.1.8 u poglavlju 5.1.2 o diskretizaciji kontinuiranih regulatora). Singularne točke regulatora s faznim prethođenjem ili kašnjenjem leže na negativnom dijelu realne osi, a u z ravnini njima odgovaraju singularne točke određene jednadžbom
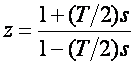(5.1.61)
pa vrijedi sljedeća veza:
a) Ukoliko je singularna točka od GC(s) s = 0, GC (z) će je imati u z= 1.
b) Ukoliko singularna točka od GC (s) teži u ∞, u GC (z) će biti u z = -1.
c) Sve singularne točke od GC (s) na negativnoj realnoj osi preslikavaju se kod GC (z) na odsječak od z = 1 do z = -1. Na pozitivni dio od z = 1 do z = 0 preslikavati će se singularne točke od GC (s) za koje vrijedi
|s| ≥(2/T).
d) Kod regulatora s faznim prethođenjem kod GC (s) vrijedi a < b, što znači da će se kod GC (z) nula n nalaziti desno od pola p, bliže točki z = 1 ( n > p ).
e) Kod regulatora s faznim kašnjenjem vrijedi a < b, što znači da će se kod GC (z) nula n nalaziti lijevo od pola p, bliže točki z = -1 (n <p).
Jednadžba diferencija diskretnih regulatora s faznim prethođenjem ili kašnjenjem dobije se iz jednadžbe (5.1.60) dijeljenjem sa z i križnim množenjem (za detalje pogledati poglavlje 6.1 Realizacija impulsne prijenosne funkcije diskretnog regulatora)
(5.1.62)
Ovom tipu regulatora vratiti ćemo se u sljedećem poglavlju u kojem analiziramo postupke projektiranja regulatora u z području. Za sada usporedimo djelovanje kontinuiranih i diskretnih regulatora s faznim prethođenjem i kašnjenjem.
Primjer:
Djelovanje regulatora s faznim prethođenjem već smo ilustrirali. Ovdje ga samo ponavljamo. Regulator prijenosne funkcije GC(s)=10(s+1)/(s+10) djeluje na sustav G(s)=10/s(s+1) selektivno, poboljšavajući dinamički dio odziva a uz to ne utječući na stabilnost, što se može vidjeti na gornjem dijelu slike 5.1.35.
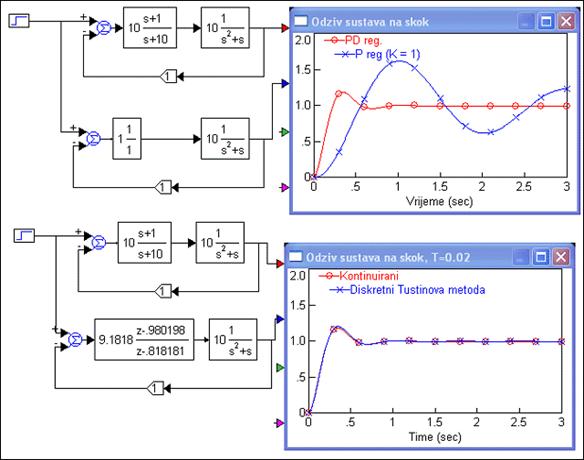
Slika 5.1.35. Regulator s faznim prethođenjem djeluje na dinamički dio odziva. Tustinova aproksimacija za T=0.02 daje skoro identični odziv
Djelovanje regulatora s faznim kašnjenjem ilustriramo na slici 5.1.36. Ovdje ga samo ponavljamo. Regulator prijenosne funkcije GC (s)=5(s+0.2)/(s+0.1) djelujući na sustav G(s)=10/(s+1) eliminira pogrešku ustaljenog stanja koju sustav ima. Diskretna realizacija Tustinovom metodom u simulacijama daje još bolji odziv.
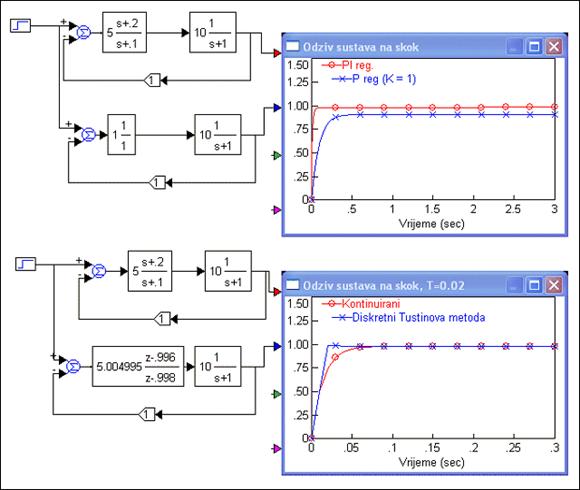
Slika 5.1.36. Regulator s faznim kašnjenjem djeluje na pogrešku ustaljenog stanja. Tustinova aproksimacija za T=0.02 daje i brži odziv