5.1. Diskretizacija kontinuiranih regulatora
Krenimo od situacije u kojoj je u kontinuiranom području proračunata prijenosna funkcija regulatora GC(s). Namjera nam je kontinuirani regulator realizirati u obliku diskretnog regulatora kojeg u z području opisujemo impulsnom prijenosnom funkcijom GC(z). Slika 5.1.1 prikazuje postavljeni zadatak.
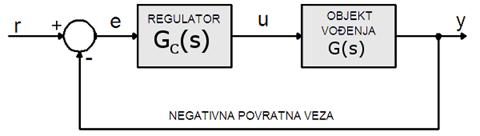
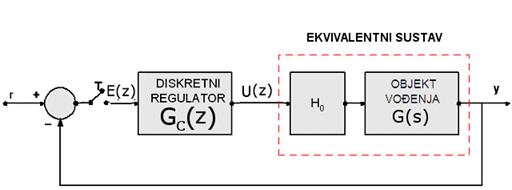
Slika 5.1.1. Diskretizacija kontinuiranog regulatora - kontinuirani regulator opisan prijenosnom funkcijom GC(s) prebacujemo u diskretni regulator impulsne prijenosne funkcije GC(z)
Želja nam je da diskretni regulator što bolje oponaša kontinuirani regulator, da im odzivi na iste pobude budu što sličniji. O tome smo puno govorili u poglavlju 3.4 Impulsna prijenosna funkcija.
Tri su načina prebacivanja kontinuirane prijenosne funkcije u diskretno područje:
a) Primjena Z – transformacije, ali ne prijenosne funkcije regulatora GC(s) već ekvivalentne prijenosne funkcije regulatora (serijskog spoja sklopa za obnavljanje i prijenosne funkcije regulatora). Postupak se engleski zove Hold Equivalent Design što hrvatski možemo prevesti kao postupak ekvivalentnog regulatora.
b) Primjena bilinearne transformacije, najčešće Tustinove transformacije kod koje se svaki s u GC(s) zamijeni odgovarajućom funkcijom od varijable z. Postupak se engleski zove Discrete Equivalent Design što bi hrvatski mogli prevesti kao postupak diskretnog ekvivalenta.
c) Primjena postupka poklapanja polova i nula kod koje se polovi i nule prijenosne funkcije GC(s) zamijene svojim diskretnim ekvivalentom iz z ravnine. Postupak se engleski zove Zero-Pole Matching i o njemu smo već govorili u poglavlju poglavlju 3.4.2.3.