5.1.1. Diskretizacija kontinuiranih regulatora postupkom ekvivalentnog regulatora
Da bi diskretni sustav što vjernije zamjenjivao kontinuirani nužno je pretpostaviti da se ispred kontinuiranog dijela nalazi sklop za obnavljanje, kako bi se na kontinuirani dio dovodio signal definiran u svim trenucima vremena, a ne diskretni signal definiran samo u trenucima uzorkovanja. U protivnom period uzorkovanja će djelovati kao ‘konstantno pojačanje’ i davati krive rezultate (za detaljnu diskusiju ovog problema pogledajte poglavlje 3.4.1 Ekvivalentni sustav). Drugim riječima to znači da GC(z) trebamo računati kao impulsnu prijenosnu funkciju serijskog spoja sklopa za obnavljanje H0(s) i kontinuirane prijenosne funkcije regulatora GC(s) kao što prikazuje slika 5.1.2. Postupak je poznat po engleskom imenu Hold Equivalent Technique što hrvatski prevodimo kao postupak ekvivalentnog regulatora.
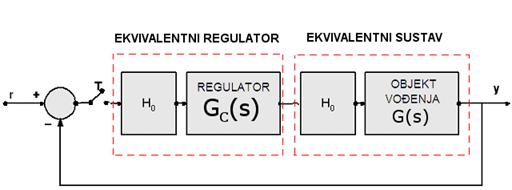
Slika 5.1.2. Impulsna prijenosne funkcije regulatora GC(z) izvodi se na temelju ekvivalentne prijenosne funkcije kontinuiranog regulatora H0GC(s)
Cijela je mudrost u tome da se ne računa Z - transformacija prijenosne funkcije GC(s), već Z - transformacija ekvivalentnog regulatora H0GC(s). U poglavlju 3.4.2.1 Razvoj na parcijalne razlomke i korištenje tablica dane su tablice upravo za ovakav proračun. Prenosimo ih i na ovom mjestu još jedanput s tim što smo sada napraviti zamjenu G(s) sa GC(s) i GE(z) s
 (5.1.1)
(5.1.1)
GC(z) je definiran razlomljenim racionalnim razlomkom:
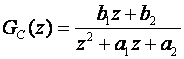

Slika 5.1.3. Impulsna prijenosna funkcija ekvivalentnog diskretnog regulatora za tipične oblike kontinuirane prijenosne funkcije regulatora GC(s)
U tablici nema prijenosne funkcije regulatora s faznim prethođenjem i kašnjenjem (PD/PI regulator) o kojima detaljnije govorimo u 5.1.4.4. Regulatori s faznim prethođenjem i kašnjenjem (PD i PI), pa pogledajmo detaljnije kako se računa njihova ekvivalentna impulsna prijenosna funkcija:

Primjer:
Za regulacijski sustav sa slike proračunaj regulator u diskretnom obliku koristeći postupak ekvivalentnog regulatora.
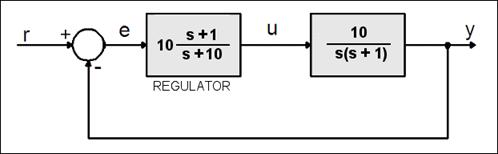
Slika 5.1.4. Kontinuirani sustav kod kojeg se regulator treba prebaciti u diskretni
U z područje prebacujemo ekvivalentni regulator. Za T=0.1 dobijemo

Slika 5.1.5 uspoređuje odzive kontinuiranog i diskretnog regulatora i odzive zatvorenog regulacijskog sustava vođenog kontinuiranim i diskretnim regulatorom za T =0.1.
Napomena: U VisSimu se mogu kombinirati diskretni i kontinuirani blokovi. Izlaz diskretnog bloka nije diskretni signal, već diskretni signal propušten kroz sklop za obnavljanje, pa sklop za obnavljanje nije nužno stavljati ispred kontinuiranog dijela sustava.

Slika 5.1.5. Usporedba kontinuiranog i diskretiziranog regulatora za T=0.1 (sinteza-ekvivalentna-funkcija.vsm)
Odziv impulsne prijenosne funkcije poklapa su u trenucima uzorkovanja s odzivom kontinuiranog regulatora, ali rezultati vođenja bitno odudaraju. Razlog je taj što je period uzorkovanja previše velik. Smanjimo li T na 0.02 novi GC(z) je:
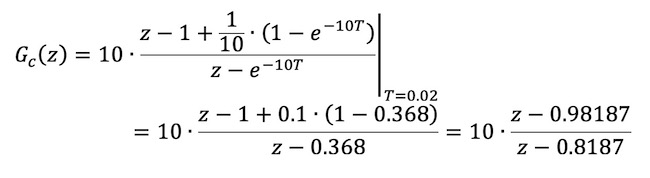
a odzive regulatora i regulacijskog sustava prikazuje slika 5.1.6.

Slika 5.1.6. Usporedba kontinuiranog i diskretiziranog regulatora za T=0.02 (sinteza-ekvivalentna-funkcija_2.vsm)
Za T = 0.02 odzivi samog regulatora i odzivi zatvorenog regulacijskog sustava vođenog kontinuiranim i diskretiziranim regulatorom su skoro identični.
Napomena:
Zanimljivo je kratko komentirati sam sustav kojeg smo analizirali (slika 5.1.4). Vođeni sustav je sustav prve vrsti drugog reda, na primjer prijenosna funkcija može predstavljati istosmjerni elektromotor kojem smo zanemarili trenje u ležajevima i induktivitet namota, a regulator je PD (proporcionalno-derivacijski) regulator kojim utječemo na prijelazni dio odziva (prebačaj, vrijeme prebačaja itd.). PD regulator selektivno djeluje ubrzavajući odziv uz zadovoljavajući iznos nadvišenja što na primjer P (proporcionalni) regulator ne može zadovoljiti.
Na primjer slika 5.1.7 prikazuje odzive kontinuiranog sustava vođenog PD regulatorom i sustava vođenog P regulatorom za dvije vrijednosti pojačanja (K=10 i K=1). Za K=10 odziv će biti jednako brz kao kod sustava vođenog PD regulatorom, ali će biti nestabilan, a za K=1 odziv će biti puno sporiji, a nadvišenje još uvijek znatno.
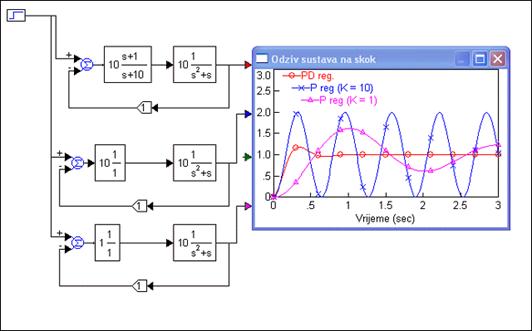
Slika 5.1.7. Usporedba kontinuiranog sustava vođenog PD i P regulatorom (sinteza-ekvivalentna-funkcija_3.vsm)
Prisjetimo li se poglavlja 3.4.2.2 Aproksimacijski postupci i jednadžbe (3.4.39), lako ćemo uočiti da je ovaj postupak identičan aproksimaciji za skokoviti signal kod koje nastojimo GC(s) prebaciti u GC(z) tako da im odzivi na skokoviti signal budu što sličniji. Transformacijska jednadžba je upravo jednadžba
 (5.1.1)
(5.1.1)
s početka ovog poglavlja.
U poglavlju 3.4.2.2 spominjali smo i aproksimaciju za pravčasti signal kod koje se GC(s) nastoji prebaciti u GC(z) tako da im odzivi na pravčasti uzlazni signal budu što sličniji. Transformacijska jednadžba je
 (5.1.2)
(5.1.2)
Međutim kako su rezultati dobiveni Tustinovom aproksimacijom (koju obrađujemo u sljedećem poglavlju) usporedivi s rezultatima aproksimacije za pravčasti signal, a Tustinov postupak je puno jednostavniji, s aproksimacijom za pravčasti signal se nećemo posebno baviti. Možemo jedino spomenuti to da su najveće razlike između impulsnih prijenosnih funkcijama dobivenim aproksimacijama za skokoviti i pravčasti signal u faznim karakteristikama diskretnog regulatora. Aproksimacija za pravčasti signal daje faznu karakteristiku puno bližu originalnoj prijenosnoj funkciji GC(s).