5.1.2. Diskretizacija kontinuiranih regulatora postupkom diskretnog ekvivalenta
Postupak diskretnog ekvivalenta engleski se naziva Discrete Equivalent Design temelji se na bilinearnoj transformaciji kojom iz s područja prelazimo u područje koje smo označili slovom z, ali se u biti ne radi o istom z području kao kod Z - transformacije. Veza između s ravnine i te 'bilinearne z ravnine' je bitno drugačija, ovisno o tome koja se bilinearna transformacija koristi.
Opći oblik pretvorbene jednadžbe bilinearne transformacije je
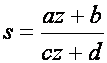(5.1.3)
a transformacija se svodi na zamjenu svih varijabli s u GC(s) izrazom oblika (5.1.1):
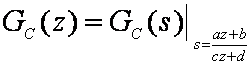(5.1.4)
(Napomena: Uočiti da se zamjena radi u GC(s) a ne u ekvivalentnoj prijenosnoj funkciji regulatora).
Tri su oblika bilinearne transformacije u upotrebi:
a) Eulerova metoda ili unaprijedna diferencija
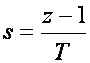(5.1.5)
b) Povratna diferencija, i
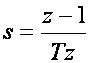(5.1.6)
c) Tustinova aproksimacija (transformacija) ili metoda trapeznog pravila
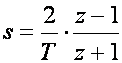(5.1.7)
Do ovih se transformacija dolazi usporedbom Laplaceove transformacije integrala i aproksimacije integrala konačnim diferencijama o čemu smo detaljno govorili u poglavlju 3.4.2.2 Aproksimacijski postupci.
Sve tri transformacije na različiti način povezuju s područje i to svoje novo područje koje smo ipak označili slovom z. Slika 5.1.8. pokazuje kako se prebacuje stabilni dio s ravnine (Re (s) < 0). Kod Eulerove metode lijevi dio s ravnine se prebaci u lijevi dio bilinearne z ravnine, kod povratne diferencije lijevi dio s ravnine se prebaci u malu kružnicu unutar jedinične kružnice, a kod Tustinove transformacije lijevi dio s ravnine se prebaci u jediničnu kružnicu bilinearne z ravnine s tim da je preslikavanje jednoznačno (sjetimo se kod Z - transformacije preslikavanje nije jednoznačno – u jediničnu se kružnicu z ravnine preslika osnovni pojas s ravnine i svi pojasevi paralelni s njim).
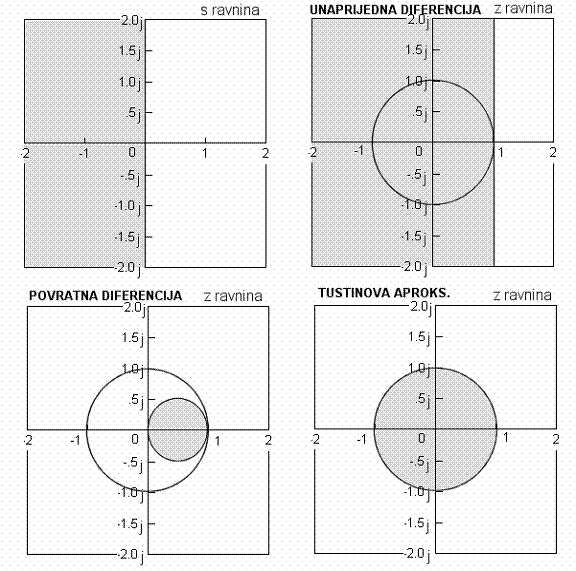
Slika 5.1.8. Preslikavanje stabilnog dijela s ravnine u 'bilinearnu z ravninu' koristeći različite transformacijske jednadžbe
Postupak diskretnog ekvivalenta je krajnje jednostavan i primjenjiv za brza ručna računanja. Pogledajmo primjer iz prethodnog poglavlja:
Primjer:
Za regulacijski sustav sa slike proračunaj regulator u diskretnom obliku koristeći postupak disketnog ekvivalenta i to Eulerovu metodu (unaprijednu diferenciju) i Tustinovu aproksimaciju (metodu trapeznog pravila) za T=0.1 i T=0.02.
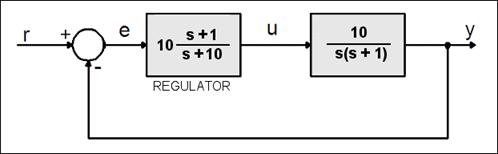
Slika 5.1.9. Kontinuirani sustav kod kojeg se regulator treba prebaciti u diskretni
Eulerova metoda daje:
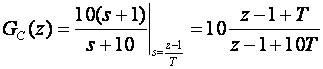
a Tustinova:
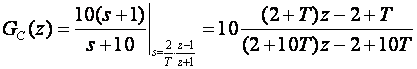
Za T=0.1 imamo:
Euler:
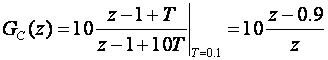
Tustin:
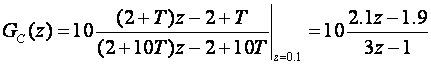
Slika 5.1.10 prikazuje odzive regulatora i odzive zatvorenog regulacijskog sustava.
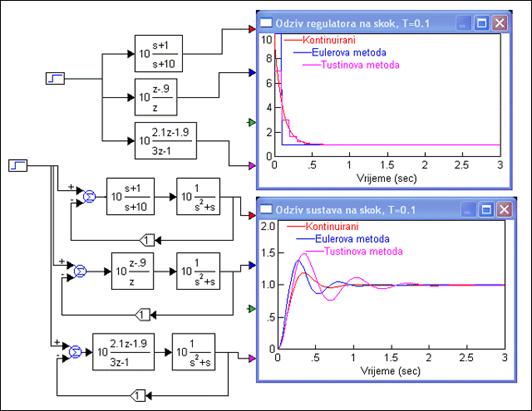
Slika 5.1.10. Usporedba kontinuiranog i diskretiziranog regulatora za T=0.1 (sinteza-diskretni-ekvivalent_1.vsm)
Zanimljivo je da Eulerova metoda daje bolji rezultat u odzivu zatvorenog regulacijskog sustava (prebačaj manji i doziv brži) od Tustinove aproksimacije.
Za T=0.02 imamo:
Euler:
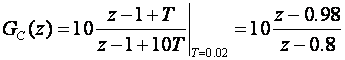
Tustin:
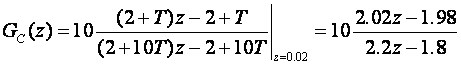
Slika 5.1.11 prikazuje odzive regulatora i odzive zatvorenog regulacijskog sustava.
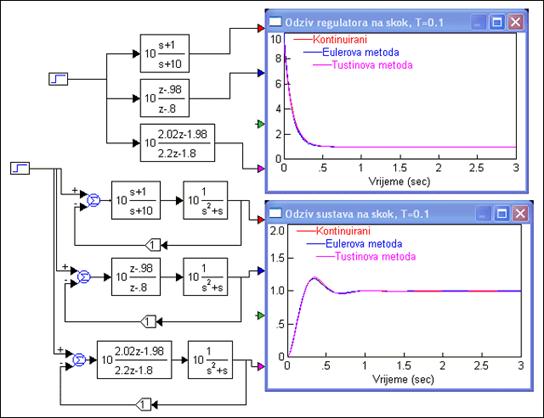
Slika 5.1.11. Usporedba kontinuiranog i diskretiziranog regulatora za T=0.02 (sinteza-diskretni-ekvivalent_2.vsm)
Za T=0.02 sva tri odziva su skoro identična.