5.1.3. Diskretizacija kontinuiranih regulatora postupkom poklapanja polova i nula
Postupak poklapanja polova i nula koji se engleski naziva Zero-Pole Matching upoznali smo već u poglavlju 3.4.2.3 Metoda poklapanja polova i nula. Sastoji se od četiri koraka:
a) Ukoliko prijenosna funkcija
regulatora GC(s) ima pol u točki s=a+jb
tada će GC(z) imati pol u točki
![]() .
.
b) Ukoliko prijenosna funkcija
regulatora GC(s) ima nulu u točki s=c+jd
tada će GC(z) imati nulu u točki
![]() .
.
c) Ukoliko prijenosna funkcija regulatora GC(s) ima nulu u beskonačnosti što znači da joj je u brojniku samo konstanta, tada će GC(z) imati nule u točki z = -1. Ponekad se jedna nula od GC(z) također ostavi u beskonačnosti čime se u pripadnu jednadžbu diferencija regulatora unese kašnjenje od jednog diskretnog trenutka.
d) Pojačanje prijenosne funkcije GC(s) za istosmjerni signal (s = 0) treba se poklapati s pojačanjem impulsne prijenosne funkcije GC(z) za z=1.
Primjer:
Za sustav iz prethodnog primjera proračunaj impulsnu prijenosnu funkciju regulatora koristeći metodu preklapanja polova i nula za T=0.1 i T=0.02.
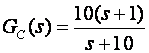
GC(z) je
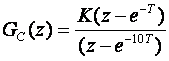
a K se računa iz izraza
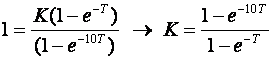
Za T = 0.1 dobiti ćemo
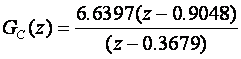
a za T = 0.02
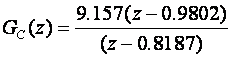
Slika 5.1.12 prikazuje usporedbu odzive regulatora i usporedbu odziva zatvorenog regulacijskog sustava.
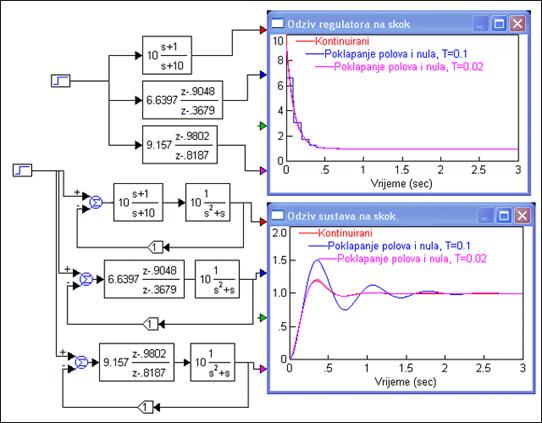
Slika 5.1.12. Usporedba kontinuiranog regulatora i diskretiziranog regulatora dobivenih postupkom poklapanja polova i nula za T=0.1 i T = 0.02 (sinteza-diskretni-poles-zeros_1.vsm)
Za T = 0.02 poklapanje je odlično, ali za T = 0.1 javlja se razlika kao i prije. Zanimljivo je usporediti ovaj postupak sa Tustinovom aproksimacijom. Prikazuje ga slika 5.1.13.
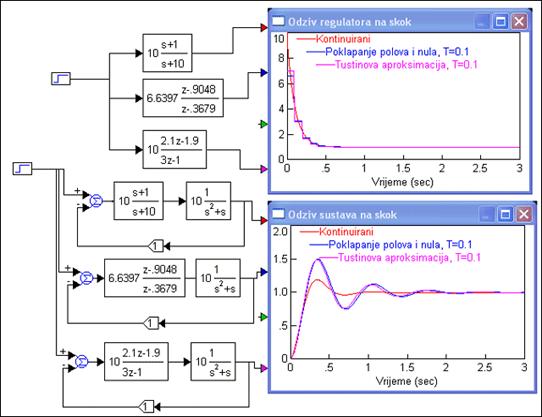
Slika 5.1.13. Usporedba kontinuiranog regulatora i diskretiziranog regulatora dobivenih postupkom poklapanja polova i nula i Tustinovom aproksimacijom za T=0.1 (sinteza-diskretni-poles-zeros_2.vsm)
Odzivi se skoro potpuno poklapaju.