5.1.4. Diskretni PID regulator
Posebno mjesto među kontinuiranim regulatorima ima PID (proporcionalno – integracijsko – derivacijski) regulator. Njegov je značaj u vođenju sustava izuzetno velik, i u analognoj primjeni prošao je cijeli niz verzija od pneumatskog, preko relejnog do tranzistorskog i integriranog. Danas su skoro sve primjene PID regulatora u digitalnom obliku koji se temelji na diskretnoj jednadžbi regulatora. Zbog toga je važno razmotriti zadatak diskretizacije PID regulatora.
Oblici PID regulatora
Osnovna jednadžba koja opisuje djelovanje PID regulatora je:
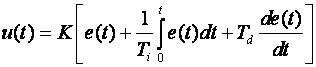(5.1.8)
i sadrži tri osnovne komponente – proporcionalnu, integracijsku i derivacijsku definirane konstantama:
- K konstanta pojačanja,
- Ti vremenska konstanta integracijskog dijela, i
- Td vremenska konstanta derivacijskog dijela.
Prebacimo li ga u Laplaceovo područje dobiti ćemo:
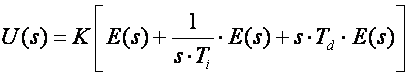(5.1.9)
Ovaj oblik algoritma PID regulatora naziva se paralelni algoritam, ali u upotrebi su i nazivi: idealni algoritam, algoritam bez međudjelovanja i ISA algoritam (eng. parallel, ideal, noninteracting, ISA algorithm) i najčešće se pojavljuje u udžbenicima. Međutim to nije jedina forma PID regulatora.
Postoji ih puno, a najčešće se susreću još dvije. Prva od njih je samo izvedenica gornje forme. Naziva se idealno paralelni algoritam, ali i neovisni algoritam ili algoritam neovisni od pojačanja (eng. ideal parallel, independent, gain independent). Dobije se tako da se sva tri člana pomnože konstantom pojačanja, te se na taj način definiraju pojačanja pojedinih članova, a ne vremenske konstante:
- konstanta pojačanja proporcionalnog dijela Kp = K ,
- konstanta pojačanja integracijskog dijela Ki = K / Ti i
- konstanta pojačanja derivacijskog dijela Kd = K . Td:
Jednadžba regulatora glasi:
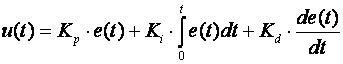(5.1.10)
Treći je oblik nešto složeniji i naziva se serijski algoritam, ali i algoritam s međudjelovanjem, analogni algoritam ili klasični algoritam (eng. series, interacting, analog, classical). Definira se jednadžbom
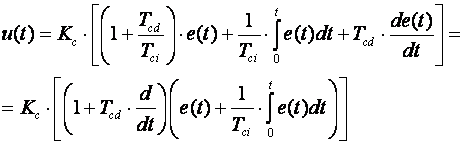
gdje su Kc, Tci i Tdi proporcionalni, integracijski i derivacijski parametri regulatora. Iz serijskog oblika u paralelni oblik prelazi se transformacijskim jednadžbama:
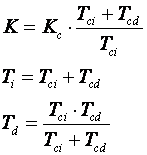(5.1.12)
U Laplaceovom području jednadžbu (5.1.11) pišemo:
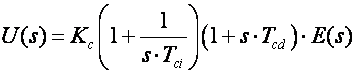(5.1.13)
Razliku između paralelnog i serijskog oblika najlakše se uoči na njihovom blokovskom prikazu nacrtanom na slici 5.1.14.
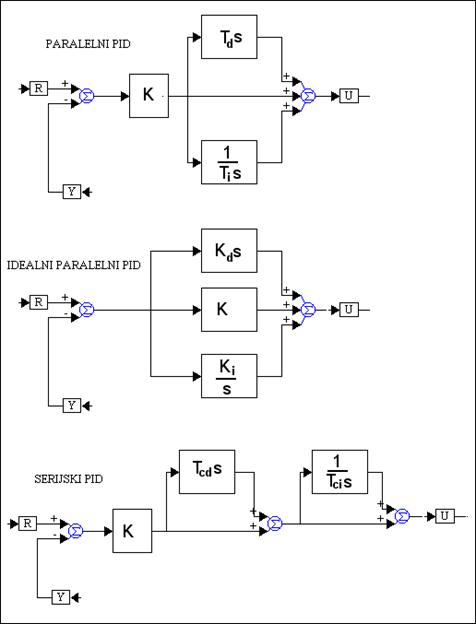
Slika 5.1.14. Blokovski prikaz paralelnog, idealno paralelnog i serijskog algoritma PID regulatora
Kako su sve tri realizacije u biti identične mi ćemo se u nastavku držati temeljne (školske) forme opisane jednadžbom (5.1.8). Transformacijskim jednadžbama lako se mogu dobiti i drugi oblici.
Naglasimo još i to da se često, a pogotovo u procesnoj industriji konstanta pojačanja iskazuje kao K=100/PB, gdje je PB tzv. proporcionalno područje ili proporcionalni opseg (eng. PB - Proportional Band) koje se izražava u postocima i predstavlja potrebnu promjenu ulaza regulatora (u postocima punog opsega) da bi se dobila 100% promjena izlazne veličine regulatora. Kako je ulaz regulatora pogreška, PB kaže koliko velik treba biti iznos pogreške (u odnosu na njenu maksimalnu vrijednost) da bi regulator na izlazu dao 100% svoje izlazne veličine.
Prije nego krenemo na zadatak diskretizacije PID regulatora, zbog njegove izuzetne važnosti, kazati ćemo par riječi o načinu njegovog djelovanja.
Djelovanje PID regulatora
PID regulator nije ništa drugo nego gruba matematička kopija postupka kojeg bi iskusni čovjek operater koristio pri vođenju.
Zamislimo primjer vođenja broda. Kormilar promatra trenutni kurs i željeni kurs u kojem bi brod trebao voziti. Na temelju njihove razlike (pogreške e(t)) on provodi upravljačku akciju – zakret lista kormila (upravljanje u(t)) koje mu je obično proporcionalno s iznosom pogreške – što je razlika između željenog i stvarnog kursa veća to će više zakrenuti kormilo (P – proporcionalno djelovanje). Upravljački signal proporcionalnog djelovanja u svakom trenutku ovisi o trenutnoj vrijednosti pogreške pa je P djelovanje vezano sa sadašnjošću, s onim što se sada događa.
Dobar kormilar neće samo promatrati pogrešku kursa broda, on će pratiti i što se s brodom događa tijekom mijenjanja kursa, on će pamtiti prošlost pogreške. Zašto? Zato da bi kod određivanja upravljačkog signala uzeo u obzir i cijeli tijek mijenjanja pogreške. Kormilar prati što se događa u prošlosti pogreške, a najgrublji matematički model prošlosti je integral. Dakle I – integracijska komponenta na neki način modelira prošlost, a kroz prošlost i iskustvo kormilara.
Treći mogući način djelovanja je pokušati predvidjeti i budućnost, pokušati predvidjeti što će se s pogreškom zbivati u budućnosti. Upravljački signal se vezuje i s onim što će se u budućnosti dogoditi, a najjednostavniji matematički model budućnosti je derivacija. Zbog toga postoji i treća D – derivacijska konstanta koja na neki način modelira budućnost, a kroz nju i intuiciju kormilara.
PID regulator je prema tome grubi matematički model pokušaja da se kod određivanja upravljačke akcije uzme u obzir i sadašnjost (P – djelovanje) i prošlost (I – djelovanje) i budućnost (D – djelovanje). Upravljački se signal formira ovisno o trenutnoj vrijednosti pogreške (P – djelovanje), ovisno o tome kako se pogreška mijenjala u prošlosti (I – djelovanje) i ovisno o tome kakav je trenutni trend porasta pogreške (D-djelovanje). Slika 5.1.14a to zorno prikazuje za primjer nezavisnog djelovanja pojedinih komponenti PID regulatora. Ne smijemo zaboraviti da kod PID regulatora sva tri dijela djeluje istovremeno, pa je upravljačka akcija rezultata njihovog zajedničkog djelovanja što unosi probleme kod određivanja konstanti regulatora.
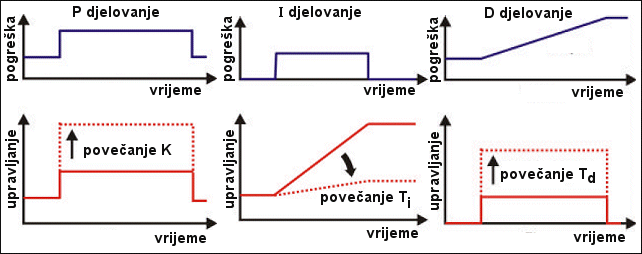
Slika 5.1.14.a Proporcionalno (P), integracijsko (I) i derivacijsko (D) djelovanje
Utjecaji proporcionalnog, integracijskog i derivacijskog dijela PID regulatora mogu se promatrati i u odnosu na specifikacije vremenskog odziva zatvorenog regulacijskog sustava. Proporcionalni član djeluje na vrijeme porasta, ali se njegovim povećanjem ne može ukloniti pogreška ustaljenog stanja. Integracijski član djeluje na smanjenje pogreške ustaljenog stanja, ali može pogoršati dinamička svojstva sustava (usporiti sustav). Derivacijski dio utječe na povećanje stabilnosti sustava, smanjuje prebačaj i poboljšava karakteristike prijelaznog dijela odziva. Kako pojedine konstante utječu na svojstva vremenskog odziva zatvorenog regulacijskog sustava sumira tablica. Prikazan je utjecaj povećanja K, smanjenja Ti i povećanja Td. Pri tome je potrebno naglasiti da se tablica uzme samo okvirno, a treba se voditi računa i o tome da su konstante međusobno ovisne. Mijenjanje jedne od njih može promijeniti tip utjecaja ostalih konstanti.
|
|
VRIJEME PORASTA |
MAKSIMALNI PREBAČAJ |
VRIJEME SMIRIVANJA |
POGREŠKE UST. STANJA |
K
|
smanjuje |
povećava |
malo utječe |
|
Ti
|
smanjuje |
povećava |
povećava |
|
Td
|
malo utječe |
smanjuje |
smanjuje |
|
Tablica 5.1. Utjecaji pojedinih parametara PID regulatora na vremenski odziv
Ponekad je dovoljno djelovati samo na statički ili samo na dinamički dio odziva, pa se definiraju varijante PID regulatora kod kojih nema derivacijskog ili integracijskog djelovanja. Takvi su regulatori poznati pod nazivom PI (proporcionalno – integracijski) i PD (proporcionalno – derivacijski) regulatori, a najjednostavnija verzija su samo P (proporcionalni) regulatori kod kojih nema ni integracijskog, ni derivacijskog djelovanja. U primjeru poglavlja 5.1.1 Diskretizacija kontinuiranih regulatora postupkom ekvivalentnog regulatora upoznali smo se s jednim takvim PD regulatorom.
Diskretizacija PID regulatora
Najjednostavniji, školski način diskretizacije PID regulatora je pretvaranje jednadžbe (5.1.8) u jednadžbu diferencija na primjer korištenjem povratne diferencije:
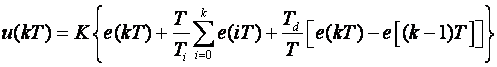(5.1.14)
Algoritam (5.1.14) naziva se pozicijski algoritam ili apsolutni algoritam (eng. positional or absolute algorithm), a ponekad se u literaturi nađe i kao nerekurzivni algoritam, zato što se kod realizacije I komponente zahtjeva poznavanje pogreške u svim prethodnim trenucima vremena. Za praktičnu realizaciju puno je korisniji brzinski, inkrementalni ili rekurzivni algoritam (eng. velocity, incremental or recursive algorithm) kod kojeg se upravljanje u trenutku kT računa na temelju upravljanja u prethodnom trenutku i prirasta upravljanja:
(5.1.15)
Izrazimo li upravljanje u prethodnom trenutku jednadžbom:
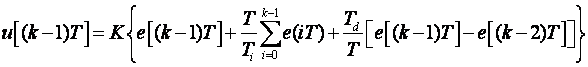(5.1.16)
prirast upravljanja možemo izračunati iz jednadžbe (5.1.15):
(5.1.17)
Nakon uvrštavanja i sređivanja dobijemo:
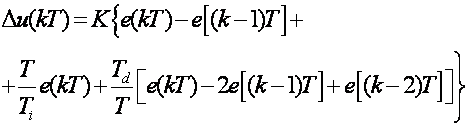(5.1.18)
Pređimo sada u z područje prikazujući kašnjenje kao množenje s negativnom potencijom varijable z:
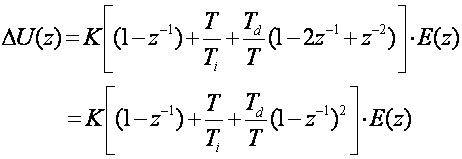(5.1.19)
Iz (5.1.17) možemo pisati
(5.1.20)
pa nakon uvrštavanja imamo:
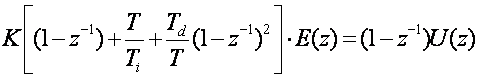(5.1.21)
i na kraju izvedemo impulsnu prijenosnu funkciju PID regulatora:
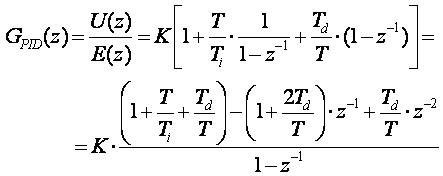(5.1.22)
Jednadžba diferencija koja opisuje ponašanje regulatora dobije se kombiniranjem jednadžbe (5.1.17) i (5.1.8):
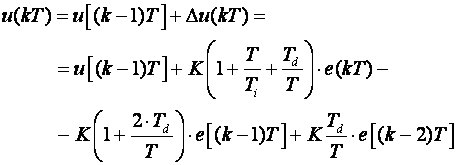(5.1.23)
Jednadžba diferencija PID regulatora je prema tome oblika
(5.1.24)
gdje su a, b i c konstante koje ovise o konstantama PID regulatora i periodu uzimanja uzoraka T. Koristeći konstante a, b i c prijenosnu funkciju (5.1.22) možemo napisati:
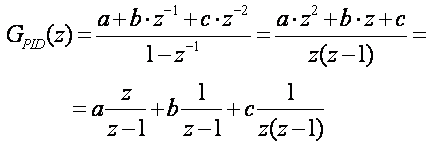(5.1.24a)
Kako postoji više načina prijelaza iz kontinuiranog u diskretno područje, ovo nije jedini način na koji se jednadžba PID regulatora može prebaciti u diskretno područje. Na primjer koristimo li trapezno pravilo kod diskretiziranja integracijskog dijela, a povratnu diferenciju kod diskretiziranja derivacije dobiju se isti oblik jednadžbe diferencija i prijenosne funkcije s tim da su sada konstante:
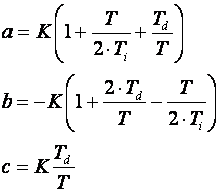(5.1.24b)