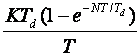5.1.4.1. Modifikacije diskretnog PID regulator
Modifikacija derivacijskog dijela regulatora dodavanjem pola na primjeru pozicijskog algoritma
Modifikacije se uvode prije svega zbog derivacijskog dijela PID regulatora. Ne zaboravimo da se derivacijski dio dodaje kako bi se djelovalo na kvalitetu dinamičkog ponašanja vođenog sustava. On će biti djelotvoran ukoliko je šum malih amplituda na srednjim frekvencijama. U tom slučaju dobro izabrani derivacijski dio može znatno povećati područje stabilnosti i omogućiti povećanje pojačanja, što daje i brži odziv. S druge strane derivacijski član jako pojačava prisutan šum. Zbog toga se derivacijske konstante trebaju pažljivo odabrati kako bi se istakli pozitivni efekti, a umanjili negativni. Najbolji način smanjenja šuma je dodavanje jednog pola derivacijskom dijelu, koji se izabere tako da djeluje kao filtar prema frekvencijama šuma. Da to pokažemo prebaciti ćemo najprije jednadžbu (5.1.8) u Laplaceovo područje:
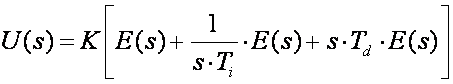 (5.1.9)
(5.1.9)
Derivacijsku nulu zamjenjujemo nulom i polom
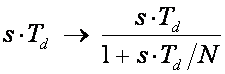
Na taj je način derivacijski član na malim frekvencijama s predviđenim derivacijskim pojačanjem, ali na velikim frekvencijama pojačanje derivacijskog člana se limitira na N. N se obično bira između 3 i 20. Prijenosna funkcija PID regulatora u s području je sada:
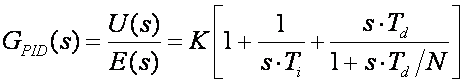 (5.1.25)
(5.1.25)
Jednadžba se može prebaciti u z područje na bilo koji od načina opisanih u ovom poglavlju. Jedan od njih je na primjer primjena Tustinove aproksimacije:
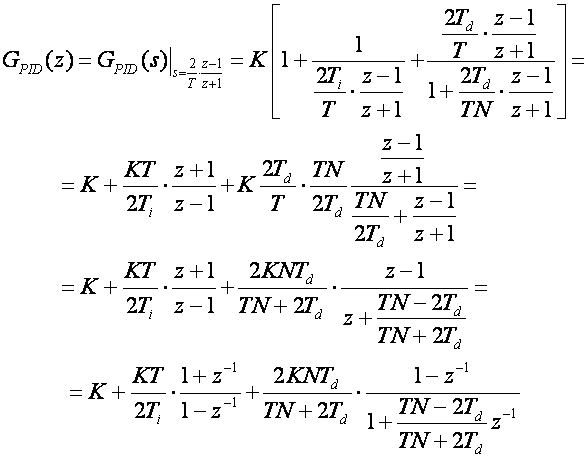
(5.1.26)
Blokovski prikaz sustava vođenog ovakvim regulatorom prikazuje slika 5.1.15.
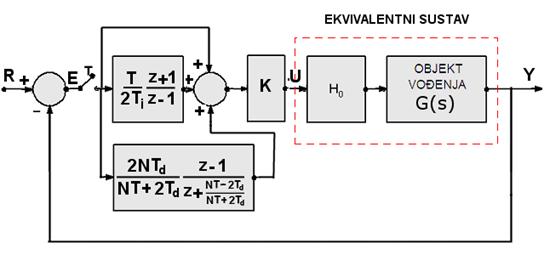
Slika 5.1.15. Blokovski prikaz
sustava vođenja s diskretnom verzijom inkrementalnog PID regulatora kod
kojeg je napravljena modifikacija derivacijskog člana dodavanjem pola te
primijenjena Tustinova aproksimacija
Modifikacija tokova signala kroz
regulator (referentna veličina prolazi samo kod integracijski dio) na
primjeru inkrementalnog algoritma
Druga modifikacija je u tome da se ne dozvoli referentnom signalu da prolazi kroz derivacijski i proporcionalni član. Modifikaciju je napravio Y.Takahashi, koji je znatan doprinos dao i u postupku podešavanja PID regulatora. To se može dobiti u slučaju kada se referentni signal ne mijenja između dva diskretna trenutka vremena. Postupak se može primijeniti i na apsolutnom i na inkrementalnom obliku algoritma. Ilustrirajmo ga na inkrementalnom algoritmu. Uvrstimo u jednadžbu inkrementalnog algoritma (5.1.17) izraz e(kT) = r(kT) – y(kT) i pretpostavimo da se r(kT) ne mijenja , što znači da je r(kT) = r[(k-1)T] = r[(k-2)T] , dobijemo
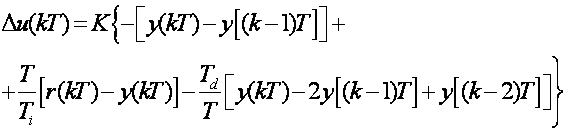 (5.1.27)
(5.1.27)
Prebacimo se u z područje
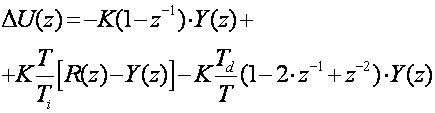 (5.1.28)
(5.1.28)
i uvrstimo (5.1.20):
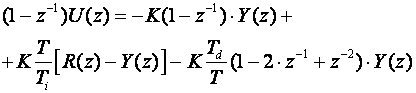 (5.1.29)
(5.1.29)
iz čega slijedi upravljački signal u z području:
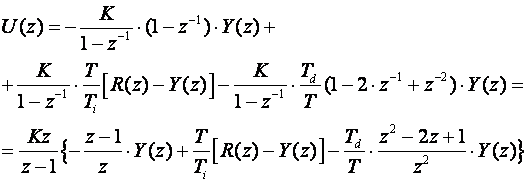 (5.1.30)
(5.1.30)
Inkrementalni oblik PID regulator opisan jednadžbom (5.1.30) blokovski možemo prikazati slikom 5.1.16.
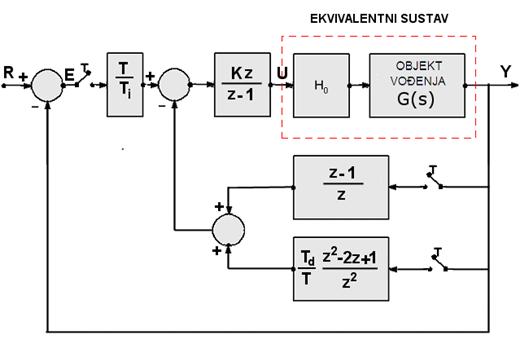
Slika 5.1.16. Blokovski prikaz sustava vođenja s diskretnom verzijom inkrementalnog PID regulatora kod kojeg je napravljena modifikacija da referentni signal ne prolazi kroz derivacijski član
Ponekad se ipak dozvoli da referentni signal prolazi kroz proporcionalni član pomnožen s konstantom proporcionalnosti kR.
Kombiniranje obje modifikacije na
primjeru pozicijskog i inkrementalnog algoritma
Naravno ova modifikacija može se kombinirati i s modifikacijom dodavanja pola derivacijskom dijelu. Ilustrirajmo ovu korekciju prethodne modifikacije i modifikacije derivacijskog člana na primjeru pozicijskog algoritma PID regulatora. Krećemo od prijenosne funkcije (5.1.25) koju ćemo vratiti u oblik (5.1.9) kod kojeg proračunavamo izlaz regulatora
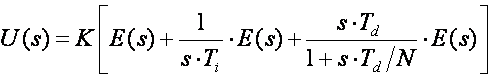 (5.1.31)
(5.1.31)
Primijenimo na to sljedeću modifikaciju kod koje ne dozvolimo referentnom signalu da prolazi kroz derivacijski član, a kod proporcionalnog člana uzimamo samo njegov dio umnoživši ga s konstantom kR. Rezultat je:
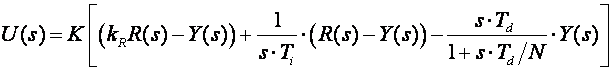 (5.1.32
(5.1.32
I ovdje možemo primijeniti bilo koju metodu diskretizacije. Kako Tustinov postupak zahtjeva puno pisanja, a oblik je relativno jednostavan primijeniti ćemo jednostavniju i direktnu metodu.
Razbijmo regulator na tri dijela: proporcionalni P(s), integracijski I(s) i derivacijski D(s):
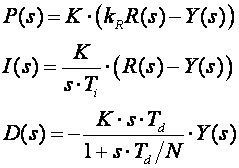 (5.1.33)
(5.1.33)
Prebacimo se natrag u vremensko područje, proporcionalni i integracijski član direktno:
![]() (5.1.34)
(5.1.34)
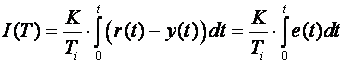 (5.1.35)
(5.1.35)
dok ćemo derivacijski član napisati u obliku diferencijalne jednadžbe:
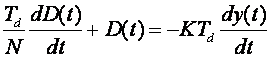 (5.1.36)
(5.1.36)
Dokaz:
U Laplaceovom području
izraz (5.1.36) daje:
 (5.1.37)
(5.1.37)
što je upravo derivacijski član.
Diskretizacija P člana je jednostavna:
![]() (5.1.38)
(5.1.38)
Kod I dijela možemo koristiti unaprijedno pravokutno, povratno pravokutno ili trapezno pravilo. Upotrijebimo povratno pravokutno pravilo:
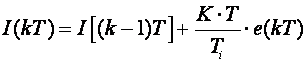 (5.1.39)
(5.1.39)
Derivacijski član ćemo diskretizirati koristeći povratnu diferenciju:
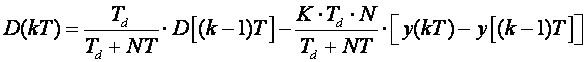 (5.1.40)
(5.1.40)
pa je jednadžba diferencija ovog oblika PID regulatora:
![]() (5.1.41)
(5.1.41)
U z području dobijemo:
![]() (5.1.42)
(5.1.42)
a pojedini članovi su
![]() (5.1.43)
(5.1.43)
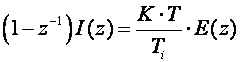 (5.1.44)
(5.1.44)
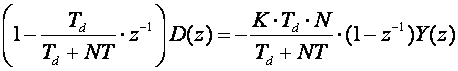 (5.1.45)
(5.1.45)
što dalje daje:
![]() (5.1.46)
(5.1.46)
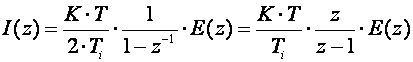 (5.1.47)
(5.1.47)
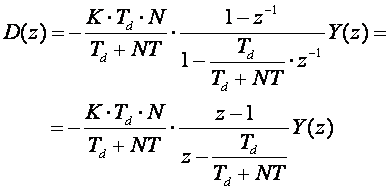 (5.1.48)
(5.1.48)
Ovaj je algoritam pozicijski ili apsolutni i shematski ga prikazuje slika 5.1.17.
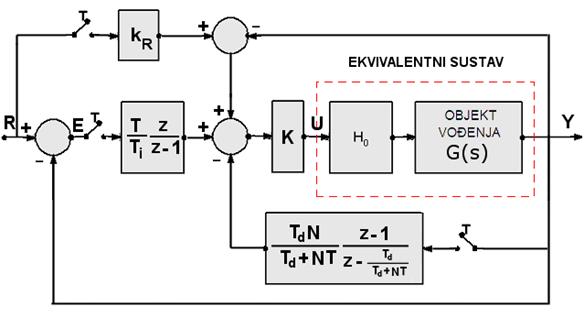
Slika 5.1.17. Blokovski prikaz sustava vođenja s diskretnom pozicijskog PID regulatora kod kojeg su napravljene obje modifikacije
PID regulator kod kojeg smo uzeli u obzir obje modifikacije je pozicijskog ili apsolutnog tipa. Inkrementalni dobijemo korištenjem jednadžbe (5.1.13), a u z području jednadžbe (5.1.16)
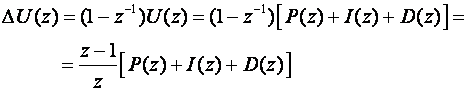 (5.1.49)
(5.1.49)
Inkrementalni oblik regulatora ne može se koristiti kao P ili PD regulator. Razlog je taj što se poništava pol u točki z=1 (vidi jednadžbu (5.1.30)) a to uzrokuje nestabilno ponašanje regulatora ukoliko se pokuša održati referentne vrijednosti.
Modifikacija zbog integracijskog
zasićenja
Jedan od problema PID regulatora je i pojava tzv. integracijskog zasićenja (eng. Integrator Windup). Javlja se kada se PID regulator koristi preko izvršnog uređaja koja ima zasićenje. Ukoliko je toliko velika da integracijski dio regulatora dovede izvršni uređaj u zasićenje, načelo povratne veze će biti narušeno zbog toga što će izvršni uređaj ostati u zasićenju iako je došlo do promjene izlaza vođenog sustava. Potrebno je dosta vremena dok integracijski dio ponovo dođe do normalnih vrijednosti. Pojava se u engleskoj literaturi zove 'Integrator Windup'. Razrješava se na više način, a jedan od njih je da se od integracijskog dijela oduzme član proporcionalan razlici ulaznog i izlaznog signala izvršnog uređaja. Konstanta proporcionalnosti je kT. Ukoliko razlike nema, nema ni njegovog doprinosa, što je razlika veća to ovaj član više smanjuje doprinos integracijskog člana. Slika 5.1.18 prikazuje intervenciju na regulatoru iz prethodnog primjera.
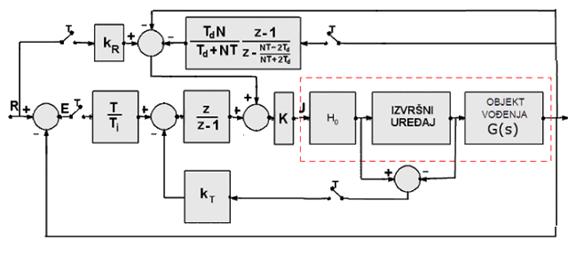
Slika 5.1.18. Blokovski prikaz intervencije u integracijski dio regulatora kojom se smanjuje utjecaj integracijskog završetka (eng. Integrator Windup) kod pozicijskog PID regulatora
Vizualizacija i realizacija
regulatora
Blokovski prikazi na slikama 5.1.15, 5.1.16, 5.1.17 i 5.1.18 samo su shematski prikaz regulatora i ne predstavljaju osnovu za realiziraju, već samo za simulaciju. Na primjer slika 5.1.19 prikazuje simulacijsku realizaciju PID regulatora prema slici 5.1.15. Regulator je dio sustava vođenja kod kojeg je dio koji se vodi drugoga reda.
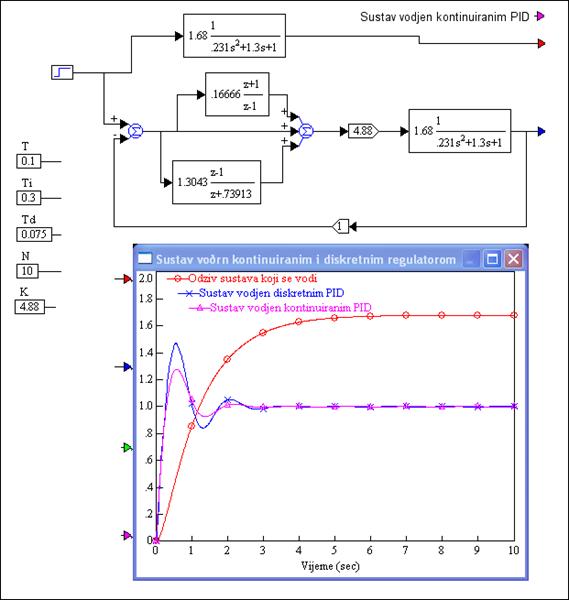
Slika 5.1.19. Primjer simulacije PID regulatora u VisSimu (PID-simulacija_standardni_oblik.vsm )
Usporedba modifikacija korekcijom derivacijskog člana i modifikacije toka signala kroz regulator prikazuje slika 5.1.20.
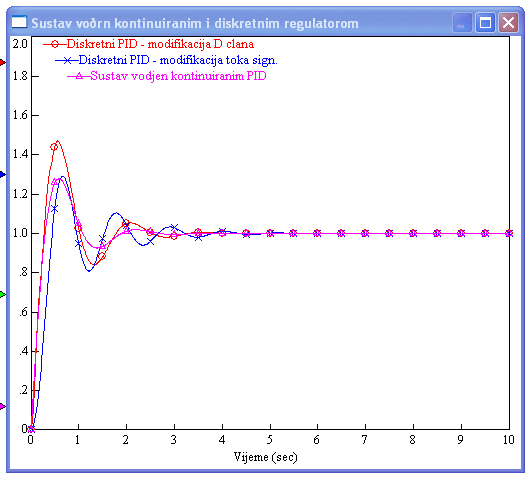
Slika 5.1.20. Usporedba sustava vođenog diskretnim PID regulatorima kod kojih su primijenjene različite modifikacije (PID-simulacija_usporedba modifikacija.vsm )
I na kraju uvedimo još i zasićenje izvršnog uređaja. Pretpostavimo da se vrijednosti upravljačke varijable smiju kretati u intervalu [0, 1]. Slika 5.1.21 prikazuje odzive kontinuiranog sustava te diskretnih sustava s i bez korekcije zasićenja integracijskog člana (kT=0.1 kR=0.2). Zanimljivo je da sustav vođen kontinuiranim PID regulatorom uz prisustvo zasićenja izvršnog uređaja ima najlošiji odziv.
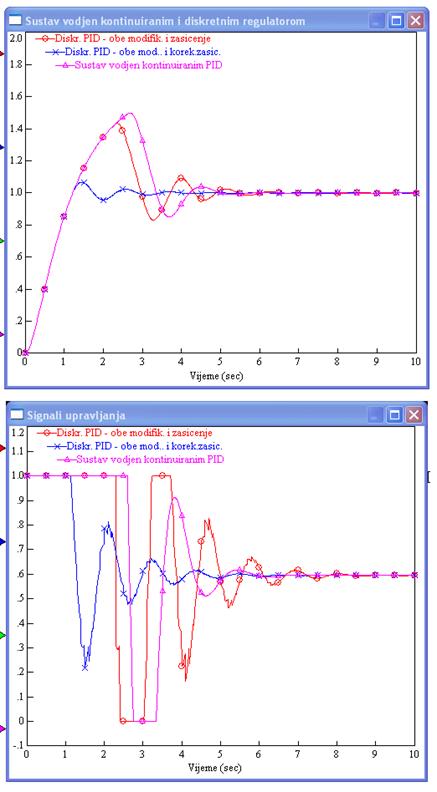
Slika 5.1.21. Usporedba sustava sa zasićenjem izvršnog uređaja za različite načine vođenja PID regulatorima – parametri isti kao na slici 5.1.19 uz kT=0.1 kR=0.2 (PID-simulacija_usporedba zasicenja.vsm)
Slika 5.1.22 prikazuje simulacijsku shemu sustava s obje modifikacije i korekcijom zasićenja.
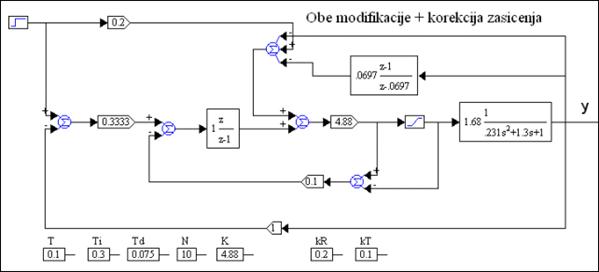
Slika 5.1.22. Simulacijska shema u VisSimu sustava obje modifikacije i korekcijom zasićenja.
Svi blokovski prikazi su bili samo načini vizualizacije različitih algoritama PID regulatora. Stvarna realizacija regulatora je uvijek jednadžba diferencija. Jednadžba diferencija je oblik regulatora koji programiramo, pa se iz impulsne prijenosne funkcije na kraju treba preći u jednadžbu diferencija (vidi poglavlje 6.1 Realizacija impulsne prijenosne funkcije diskretnog regulatora ) ili ukoliko nas analiza i simulacija ne zanimaju impulsnu prijenosnu funkciju ne trebamo niti izvoditi. Na primjer kod algoritma s obje modifikacije jednadžba (5.1.41) je polazna jednadžba koju programiramo, ali ona je dobivena za određeni oblik diskretizacije kontinuirane jednadžbe. Napišimo i opći oblik jednadžbe diferencija diskretnog PID regulatora:
![]() (5.1.50)
(5.1.50)
a pojedini članovi su u općem slučaju oblika
![]() (5.1.51)
(5.1.51)
![]() (5.1.52)
(5.1.52)
![]() (5.1.53)
(5.1.53)
Koeficijenti kP1, kP2, kI1, kI2, kD1 i kD2 ovise o načinu prijelaza iz kontinuiranog u diskretno područje. Kod jednadžbi (5.1.39) i (5.1.40) koristili smo kod integracijskog člana aproksimaciju integrala unaprijednim pravokutnim pravilom, a za aproksimaciju derivacije u derivacijskom članu povratnu diferenciju.
Tablica 5.2 sumira vrijednosti koeficijenata za različite načine diskretizacije. Vrijednosti proporcionalnih koeficijenata su uvijek iste i neovisne o diskretizaciji.
Proporcionalni član
|
kP1 |
K kR |
|
kP2 |
K |
Integracijski član
|
|
Unaprijedno pravokutno |
Povratno pravokutno |
Trapezno |
|
kI1 |
0 |
K T /Ti |
K T /2 Ti |
|
kI2 |
K T /Ti |
0 |
K T /2 Ti |
Derivacijski član
|
|
Unaprijedna diferencija |
Povratna diferencija |
Tustinova aprox. |
Aprox. za pravčasti signal |
|
kD1 |
1 – N T / Td |
Td /( Td + NT) |
2Td –NT |
|
|
kD2 |
K N |
KNTd /( Td + NT) |
2KTd N |
|
Tablica 5.2. Koeficijenti jednadžbe diferencija diskretnog PID regulatora oblika definiranog jednadžbama (5.1.50) - (5.1.53)