Zadatak realizacije je jasan. Regulator je proračunat i izražen impulsnom prijenosnom funkcijom oblika:

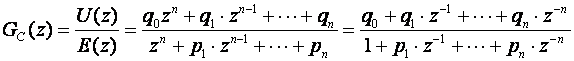      (6.1.1)

Zanima nas kako proračunati izlazni diskretni signal u(kT) na temelju poznavanja slijeda ulaznog diskretnog signala e(kT), e[(k-1)T], ..., e[(k-n)T] i eventualno slijeda izlaznog diskretnog signala u prošlim trenucima vremena u[(k-1)T], u[(k-2)T], ..., u[(k-n)T]. Ukoliko se pri proračunu koristi samo slijed ulaznih diskretnih signala postupak realizacije nazivamo nerekurzivni, a ukoliko se koristi i slijed ulaznih signala i slijed izlaznog diskretnog signala u prošlim trenucima vremena postupak je rekurzivni.

Ovaj je zadatak važan i detaljno obrađen u teoriji digitalne obrade signala i teoriji digitalnih filtera. U prošlom smo poglavlju pokazali da digitalni regulator u biti i nije ništa drugo nego digitalni filter, pa nam samo ostaje primijeniti znanja o realizaciji digitalnih filtera. Pri tome ćemo naglasak dati na one postupke koji su direktno vezani s realizacijom impulsne prijenosne funkcije regulatora.

Tri su osnovna načina realizacije impulsne prijenosne funkcije, dva nerekurzivna, što znači da kod proračuna u(kT) koriste samo ulazni signal i jedan rekurzivni koji u proračunu koristi i prošle vrijednosti izlaznog signala. On se ujedno tako i zove. Postupci realizacije su:

a) Realizacija konvolucijskim algoritmom,

b) Realizacija algoritmom temeljenim na diskretnoj Fourierovoj transformaciji (DFT), i

c) Realizacija rekurzivnim algoritmom.

Prva su dva algoritma primjerenija digitalnoj obradi signala pa ćemo ih ovdje samo kratko spomenuti. Realizacija digitalnih regulatora provodi se uglavnom rekurzivnim algoritmima kod kojih se impulsna prijenosna funkcija pretvara u jednadžbu diferencija, pa ćemo se njima najviše i baviti.

6.1.1.  Konvolucijski algoritam

Njega smo u biti već upoznali.  U poglavlju 3.4.1 o ekvivalentnom sustavu  spomenuli smo konvolucijsku jednadžbu (3.4.16) kojom proračunavamo vrijednost signala u trenutku kT koju ćemo sada napisati malo drugačije:

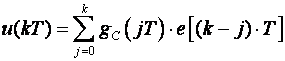                              (6.1.2)

Vrijednost izlaznog signala u trenutku kT proračunavamo na temelju poznavanja slijeda ulaznog signala do trenutka kT, tj. e(0), e(T), ..., e[(k-1)T] i diskretnog impulsnog odziva sustava  g_C(jT) (odziva diskretnog sustava na impulsnu Diracovu pobudu).

Ovisno o tome da li je diskretni impulsni odziv g_C(jT) konačan ili beskonačan diskretne sustave dijelimo na:

a) sustave s konačnim impulsnim odzivom (FIR – eng. Finite Impulse Response), i

b) sustave s beskonačnim impulsnim odzivom (IIR – eng. Infinite Impulse Response).

Kod sustava s konačnim impulsnim odzivom (FIR sustavi) g_C(jT) je različit od nule samo za vrijednosti varijable j koje pripadaju zatvorenom intervalu [J₁,J₂], a kod sustava s beskonačnim impulsnim odzivom (IIR sustavi) g_C(jT) je uvijek različit od nule. Sjetimo li se međutim razmišljanja o stabilnosti diskretnih sustava znamo da će sustav biti stabilan samo ukoliko je:

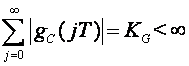
a to će biti ispunjeno onda i samo onda ukoliko g_C(jT) teži nuli kada j teži u beskonačno (na primjer g_C(jT) = a^j , gdje je |a| < 1).

Diskretne sustave FIR tipa u z području prikazujemo impulsnom prijenosnom funkcijom:

      (6.1.3)

dok diskretne sustave IIR tipa u općem slučaju prikazujemo impulsnom prijenosnom funkcijom oblika (6.1.1). U teoriji diskretnog vođenja više se pojavljuju diskretni regulatori IIR tipa, iako nije isključena niti pojava regulatora FIR tipa, ali u principu diskretni se regulator više promatra u svijetlu svog faznog doprinosa (regulatori s faznim prethođenjem i faznim kašnjenjem) ili karaktera (PI, PD, PID regulatori) nego li u svijetlu karakteristika njihovog impulsnog odziva, pa se pojmovi FIR ili IIR regulator nikada ni ne spominju. Ipak važno je imati i znanja o diskretnim sustavima promatranim kao FIR ili IIR sustavi.  Oni su nezaobilazni u teoriji digitalne obrade signala i teoriji digitalnih filtera, a kako su digitalni filteri važni u digitalnom vođenju u dodatku A4 Temeljni pojmovi teorije digitalnih filtera FIR i IIR tipa dat ćemo kratak osvrt na njih i načine njihovog projektiranja.

Za sada spomenimo samo to da konvolucijski algoritmi i nisu pogodni za realizaciju diskretnih sustava IIR tipa iz jednostavnog razloga što povećanjem diskretnog trenutka vremena jT raste i broj potrebnih operacija množenja prema jednadžbi (6.1.2). Na primjer pretpostavimo da je period uzorkovanja T=0.1 ms. Za proračun izlaznog diskretnog signala nakon 1 sekunde trebalo bi napraviti 10.000 množenja, što je u realnom vremenu teško izvodivo. Možemo ga aproksimirati ograničavanjem broja članova impulsnog odziva ali se to obično ne koristi zato što postoje i drugi načini realizacije diskretnog sustava.

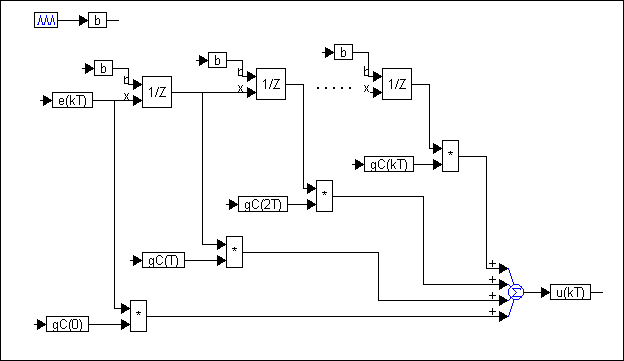
Kazali smo da je konvolucijski algoritam nerekurzivni algoritam što se najbolje može vidjeti iz njegovog blokovskog prikaza (blok 1/z predstavlja jedinično kašnjenje), slika 6.1.1.
 

Slika 6.1.1. Realizacija diskretnog sustava konvolucijskim algoritmom

.: Sljedeća stranica > Algoritam temeljen na diskretnoj Fourierovoj transformaciji (DFT)