I ovaj se algoritam primjenjuje pretežno u digitalnoj obradi signala, pa ćemo ga samo kratko spomenuti. Ideja je prenesena iz kontinuiranog područja. Pretpostavimo da imamo prijenosnu funkciju G_C(s) i njenu frekvencijsku karakteristiku G_C(jω). Ukoliko nam je poznat frekvencijski spektar (Fourierova transformacija) ulaznog signala E(jω), frekvencijski spektar (Fourierovu transformaciju) izlaznog signala jednostavno izračunamo produktom U(jω) = G_C(jω) E(jω). Množenje u frekvencijskom području odgovara konvoluciji u vremenskom području pa je:

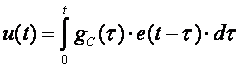              (6.1.4)

U diskretnom području umjesto Fourierove transformacije imamo diskretnu Fourierovu transformaciju (DFT) koja se za slijed od N ulaznih diskretnih signala e(nT), n=0, 1, ..., N-1 računa izrazom:

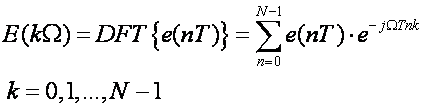              (6.1.5)

gdje je Ω = 2π/NT period uzimanja uzoraka u frekvencijskom području, a T je period uzimanja uzoraka u vremenskom području.

Na sličan način odredi se i diskretna Fourierova transformacija odziva diskretnog sustava na Diracovu pobudu:

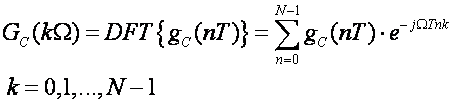              (6.1.6)

Može se pokazati (i dokazati) da će u određenim uvjetima vrijediti

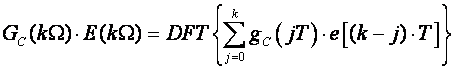              (6.1.7)

a izraz u zagradi prema jednadžbi (6.1.2) nije ništa drugo nego u(kT).

Realizacija diskretnog sustava DFT-om se prema tome sastoji od tri koraka:

a) Računanje diskretne Fourierove transformacije jednadžbom (6.1.5), za slijed od N ulaznih diskretnih  signala e(nT), n=0, 1, ..., N-1.

b) Računanje diskretne Fourierove transformacije odziva diskretnog sustava na Diracovu pobudu jednadžbom (6.1.6).

c) Proračun inverzne diskretne Fourierove transformacije produkta G_C(kΩ) E(kΩ):

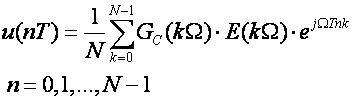              (6.1.8)

Cijela se realizacija temelji na DFT-u - diskretnoj Fourierovoj transformaciji. Razvojem algoritma brzog proračuna diskretne Fourierove transformacije (FFT – eng. Fast Fourier Transform), otvorena su široka vrata primjeni DFT-a u realizaciji diskretnih sustava. Algoritama FFT-a i literature o njemu ima puno, a napomenimo samo još to da je na tržištu cijeli niz sklopova, tzv. signal procesora kojima se FFT jednostavno implementira.

U realizaciji diskretnog regulatora i njegovom prebacivanju u oblik digitalnog regulatora ipak su najvažniji rekurzivni algoritmi koje razmatramo u sljedećem poglavlju. Ovdje navodimo samo nekoliko poveznica prema Web prikazima posvećenim DFT-u i FFT-u: 

- Discrete Fourier Transform and the FFT http://www.cage.curtin.edu.au/mechanical/info/vibrations/tut4.htm

- Fast Fourier Transform Tutorial http://www.spd.eee.strath.ac.uk/~interact/fourier/fft.html

- Fourier and the Frequency Domain http://www.spd.eee.strath.ac.uk/~interact/fourier/fourier.html

- Digital Signal Processing http://www.newwaveinstruments.com/resources/rf_microwave_resources/sections/digital_signal_processing_dsp_tutorial_software.htm

- FFT Links - http://www.fftw.org/links.html