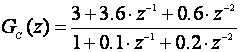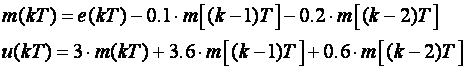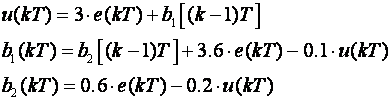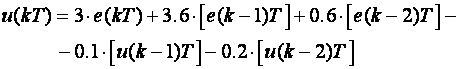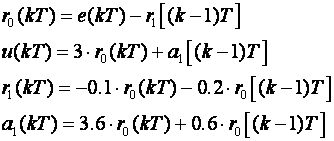6.1.3. Rekurzivni algoritam
Cilj: Naučiti rekurzivni algoritam koji se u realizaciji
digitalnog vođenja najviše i koristi.
Konvolucijski i DFT algoritam spada u nerekurzivne realizacije zato što se izlazni diskretni signal u(kT) računa samo na temelju slijeda ulaznih diskretnih signala, dok se kod rekurzivnog algoritma u proračunu vrijednosti izlaznog signala u(kT) u trenutku kT koristi slijed ulaznog signala e(kT), e[(k-1)T], ... , e[(k-n)T] i slijed prošlosti izlaznog signala u[(k-1)T], ... , u[(k-n)T]. Opet krećemo od impulsne prijenosne funkcije (6.1.1):
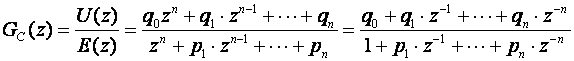(6.1.1)
Krajnji cilj nam je jednadžba diferencija izraz za u(kT), a do njega možemo doći na četiri osnovna načina:
a) direktnom realizacijom,
b) serijskom (kaskadnom) realizacijom,
c) paralelnom realizacijom, i
d) ljestvičastom realizacijom.
Konačan rezultat realizacije jednadžba diferencija prikazana grafički često se zove i struktura digitalnog regulatora, odnosno struktura digitalnog filtera (eng. Digital Filter Structurs), pa ćemo taj naziv i ovdje zadržati. Napomenimo i to da su rekurzivni algoritmi posebno pogodni i za realizaciju digitalnih filtera IIR tipa (eng. Infinite Impulse Response), ali o tome više kasnije.
U nastavku ćemo najprije opisati sve strukture i načine realizacije, a zatim ćemo dati komentar o kriterijima za izbor odgovarajuće strukture realizacije.
Krenimo od direktne realizacije.
6.1.3.1. Direktna realizacija
Direktna realizacija je ujedno i najjednostavnija. Polazna točka joj je impulsna prijenosna funkcija oblika (6.1.1), a do jednadžbe diferencija možemo doći na četiri različita načina, koji daju četiri direktne strukture (eng. Direct Structure):
a) prvu ili 1D strukturu,
b) drugu ili 2D strukturu,
c) treću ili 3D strukturu, i
d) četvrtu ili 4D strukturu.
Prva direktna struktura (1D)
Krećemo od jednadžbe (6.1.1), i uvodimo pomoćnu varijablu M(z):
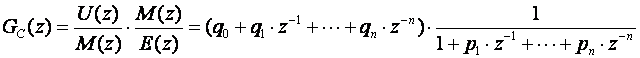(6.1.9)
pa možemo pisati:
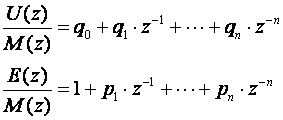(6.1.10)
Dalje imamo:
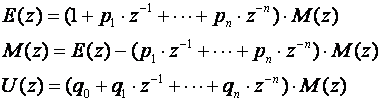(6.1.11)
pa jednadžbe diferencija glase:
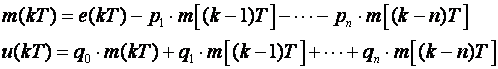(6.1.12)
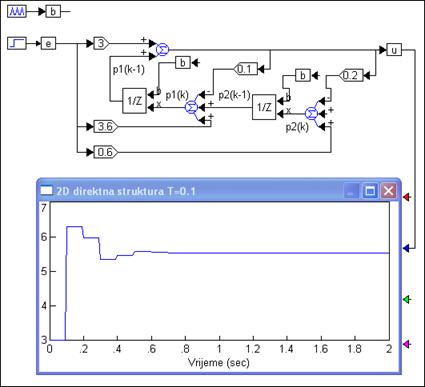
1D struktura se naziva kanonska zato što u realizaciji koristi samo n jedinica za kašnjenje, što je minimalni potrebni broj da bi se realizirala impulsna prijenosna funkcija n-tog reda.
Primjer:
Za primjer ćemo uzeti sustav drugog reda:
Jednadžbe diferencija glase:
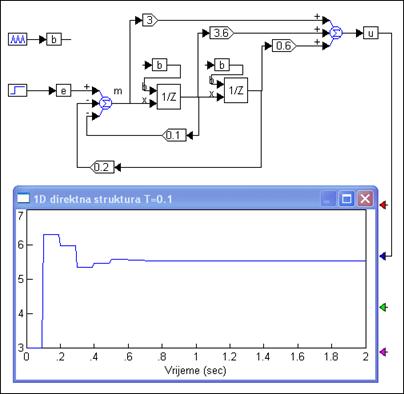
Strukturu blokovski možemo prikazati slikom 6.1.2. gdje blok 1/z predstavlja jedinično kašnjenje.
Slika 6.1.2. Realizacija diskretnog regulatora prvom direktnom strukturom (1D) i odziv na jedinični skok (1D-struktura.vsm)
Druga direktna struktura (2D)
Druga direktna struktura je transponirana 1D struktura. Isto je tako kanonska, ali zahtjeva (n+1) sumacijski element, za razliku od 1D strukture koja ih je zahtijevala samo 2. Jednadžbe diferencija koje je opisuju su:
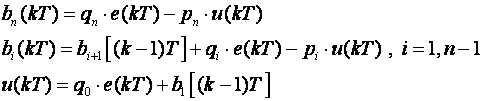(6.1.13)
Primjer:
Uzeti ćemo opet isti primjer sustava drugog reda:
Jednadžbe diferencija glase:
Blokovski prikaz ove realizacije prikazuje slika 6.1.3.
Slika 6.1.3. Realizacija diskretnog regulatora drugom direktnom strukturom (2D) i odziv na jedinični skok (2D-struktura.vsm)
Treća direktna struktura (3D)
Nju smo u biti već upoznali. Sastoji se u križnom množenju impulsne prijenosne funkcije te nakon toga primjeni teorema pomaka Z transformacije:
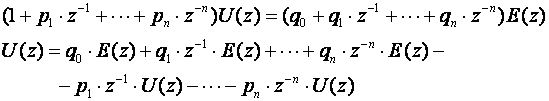(6.1.14)
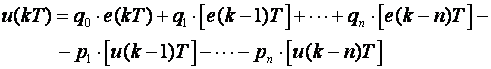(6.1.15)
Primjer:
Ponovo ista impulsna prijenosna funkcija
Jednadžba diferencija glasi
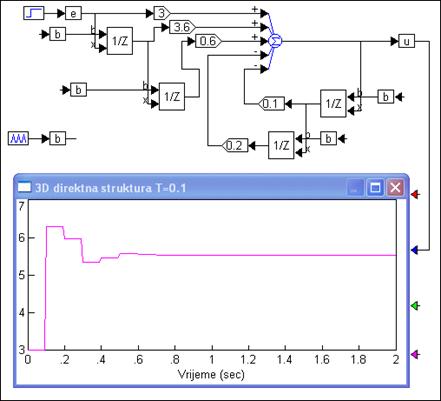
Strukturu blokovski možemo prikazati slikom 6.1.4. Struktura ima samo jedan sumator, ali zato ima 2n elemenata za kašnjenje.
Slika 6.1.4 Realizacija diskretnog regulatora trećom, direktnom strukturom (3D) i odziv na jedinični skok (3D-struktura.vsm)
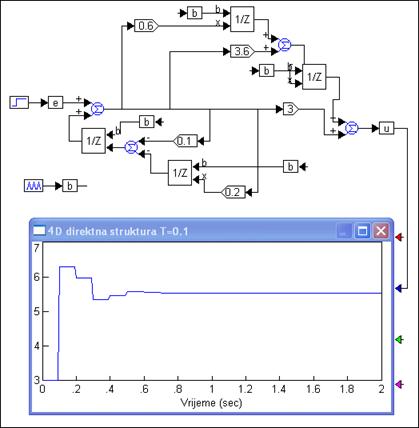
Četvrta direktna struktura (4D)
Četvrta direktna struktura je transponirana 3D struktura. Ima 2n elemenata za kašnjenje i 3n sumatora. Opisuju je 2n jednadžbi diferencija:
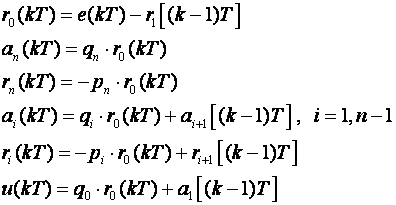(6.1.16)
Primjer:
Za sustav drugog reda
jednadžbe diferencija glase:
Strukturu blokovski možemo prikazati slikom 6.1.5.
Slika 6.1.5. Realizacija diskretnog regulatora četvrtom direktnom strukturom (4D) i odziv na jedinični skok (4D-struktura.vsm)
Kod 1D i 2D strukture broj elemenata za kašnjenje je n, a kod 3D i 4D duplo veći 2n. Što je manji broj elemenata za kašnjenje to je manje zauzeće memorije, ali u današnjim računalima memorija nije skupa. Broj sumatora je najmanji kod 3D strukture koja treba samo 1 sumator. 1D struktura treba 2 sumatora, 2D struktura n+1, a 4D struktura čak 2n sumatora. Najveći nedostatak svih direktnih struktura je velika osjetljivost na vrijednosti koeficijenata pi i qi, posebno za veliki n. Male promjene vrijednosti ovih koeficijenata uzrokuju velike promjene u položaju nula i polova impulsne prijenosne funkcije. To je posebno kritično kada se regulator realizira na računalu ograničenih mogućnosti, gdje je ograničen broj bitova kojima prikazujemo parametre. U tom je slučaju nužno zaokruživanje, a zaokruživanje unosi pogrešku vrijednosti parametara na koju su direktne strukture osjetljive.
Zbog toga se,
pogotovo za sustave većeg reda definiraju i drugi tipovi realizacije:
serijska, paralelna i ljestvičasta, ali ni ova treća nije baš pogodna za
realizaciju. Ostaju serijska i paralelna kod kojih je osjetljivost na
varijacije koeficijenata povoljnija.