Digitalno vođenje on-line (FESB, Split)

5.1.4.2. Primjer programske realizacije diskretnog PID regulatora

Cilj: Naučiti kako treba izgledati program koji računa upravljačku veličinu na temelju algoritma PID regulatora sa svim modifikacijama.

Digitalna implementacije PID regulatora temelji se na šest osnovnih koraka:

1. Čekanje signala sata kojim se definira period uzorkovanja.

2. Čitanje ulaznih vrijednosti: izlaza s A/D pretvarača i referentne vrijednosti izlaza iz memorije.

3. Proračun signala upravljanja.

4. Slanje signala upravljanja na D/A izlaz.

5. Postavljanje novih vrijednosti internih varijabli regulatora.

6. Odlazak na korak br. 1.

Osim toga obično se prije dolaska na korak br. 1 proračunaju sve konstante koje ovise o postavljenim vrijednostima regulatora.

U nastavku ćemo navesti kôd PID regulatora u pseudo-kôdu sličnom simulacijskim jezicima. Kôd se odnosi na algoritam kod kojeg je napravljena modifikacija derivacijskog člana, modifikacija toka signala, korekcija zasićenja i korekcija zbog promjene parametara tijekom vođenja (što detaljnije komentiramo iza koda), te aproksimacija integrala povratnim pravokutnim pravilom, a derivacije povratnom diferencijom. Polazna jednadžba je jednadžba diferencija

(5.1.49)

i njoj pridružene jednadžbe za proračun pojedinih članova:

(5.1.50)

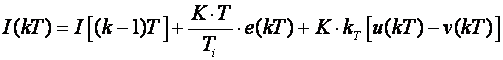(5.1.51)

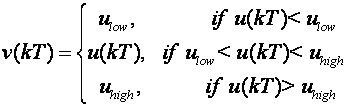(5.1.52)

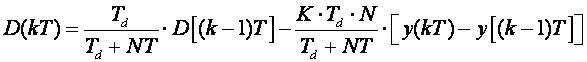(5.1.53)

U skladu s tablicom 5.2 lako je napisati jednadžbe i za ostale oblike diskretizacije.

Program ima tri interna stanja – nI, nD i yold koja se ažuriraju u svakom diskretnom trenutku vremena. Navedimo najprije kod, a na kraju ćemo dati kratki komentar.

'PID regulator'

'Definicija varijabli'

r 'referentna veličina'

y 'izlazna (regulirana) veličina'

yold 'prethodna izlazna veličina'

u 'upravljanje prije zasićenja'

v 'upravljanje - izlaz regulatora'

P 'proporcionalni dio'

nI 'integracijski dio – interna varijabla'

nD 'derivacijski dio– interna varijabla'

t 'vrijeme'

INIT

'Početni uvjeti (računaju se samo na početku)'

nI=I0

nD=D0

u=u0

v=v0

'Početno postavljanje vrijednosti yold'

INPUT y

yold=y

'A može se i definirati neka početna vrijednost y0'

'Proračun konstanti (računa se samo kod promjene parametara)'

Kp=K*kR

Ki1=K*T/Ti

Ki2=K*kT

Kd1=Td/(Td+N*T)

Kd2=K*Td*N*T/(Td+N*T)

'Bumpless transfer – računa se samo kod promjene parametara'

nI=nI+Kold*(kRold*r-y)-Knew*(kRnew*r-y)

'Algoritam'

'Zabilježi vrijeme'

t=t

BEGIN

'Učitavanje ulaznih vrijednosti'

INPUT r

INPUT y

'Proporcionalni dio'

P=Kp*r-K*y

'Integracijski dio'

nI=nI+Ki1*(r-y)-Ki2*(u-v)

'U prvom koraku uzmu se početne vrijednosti upravljanja u i v, a nakon toga vrijednosti prethodnog trenutka što unosi određenu pogrešku'

'Derivacijski dio'

nD=Kd1*nD-Kd2*(y-yold)

'Proračun upravljanja'

u=P+nI+nD

v=IF u<ulow THEN ulow

ELSE IF u<uhigh THEN u

ELSE uhigh

OUTPUT v

'Novi parametri'

yold=y

'Čekaj dok prođe period uzorkovanja'

WAIT UNTIL t=t+T

REPEAT

'Parametri'

K=4.88 'konstanta pojačanja'

Ti=0.3 'vrem.konstanta integracijskog dijela'

Td=0.075 'vrem.konstanta derivacijskog dijela'

N=10 'konst.dodatnog derivacijskog pola'

kR=0.2 'dio reference koji ide kroz P član'

kT=0.1 'konst. korekcije integ. zasićenja'

ulow=0 'najmanja dopuštena vrij. upravljanja'

uhigh=1 'najveća dopuštena vrij. upravljanja'

T=0.1 'period uzorkovanja'

'Početne vrijednosti'

I0=0 'početna vrijednost integ. člana'

D0=0 'početna vrijednost deriv. člana'

u0=0 'početna vrijednost upravljanja'

v0=0 'početna vrijed. zasićenog upr.'

'Može biti zadan i početni y0'

Proračun između oznaka INIT i BEGIN radi se samo jedan put i potrebno je ponoviti dio iza 'proračun konstanti' samo ukoliko se promijene vrijednosti parametara regulatora. Međutim ukoliko je k_R različit od 1 tada proporcionalni član (5.1.50) nije jednak nuli u stacionarnom stanju. Kako bi se osiguralo da promjena parametara u trenutku kada se sustav nalazi u nekom stacionarnom stanju ne uzrokuje nagle promjene u sustavu (u eng. govornom području pojava se zove bumpless parameter change) treba se nastojati da veličina I + P bude neovisna na promjene parametara, a to se postiže tako da se trenutna zatečena vrijednost integracijskog dijela I promjeni s novim I (I_novi) kojeg proračunamo jednadžbom:

(5.1.54)

i već smo ga uključili u algoritam.

Sličan problem se javlja i kod komercijalnih PID regulatora kod prelaska iz automatskog načina rada u ručni. Komercijalni PID regulatori obično imaju dva režima rada automatski (Aut) i ručni (Man). Prijelaz iz jednog načina rada u drugi može se napraviti bilo kad tijekom vođenja sustava. Problem se može javiti ukoliko je regulator pozicijskog tipa s obzirom da integracijski dio ima neku akumuliranu vrijednost. Kod inkrementalnog oblika problem nije toliko značajan zato što je utjecaj prelaska s Aut na Man samo u jednom inkrementalnom ciklusu. Problem se naziva u eng. govornom području bumpless transfer i rješava se posebnim konstrukcijama PID regulatora. Slika 5.1.23 prikazuje simulaciju prednjeg panela industrijskog PID regulatora.

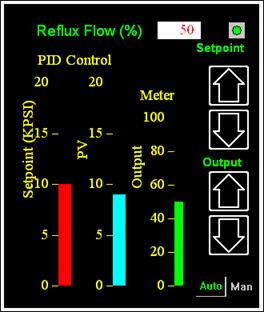
Slika 5.1.23. Simulacija prednjeg panela industrijskog PID regulatora (Pidplate.vsm)

Najvažniji korak u projektiranju sustava vođenja temeljenog na PID regulatoru je određivanje parametara regulatora. Egzaktne metode se uče u okviru temeljnih kolegija automatske regulacije. Na ovom nas mjestu zanimaju prije svega eksperimentalne metode podešavanja parametara o kojima se govori u sljedećem poglavlju.