5.5.1.1. Odabir željenog položaja polova zatvorenog regulacijskog sustava
Najčešće tako da definiramo željeno ponašanje sustava postavljanjem specifikacija u vremenskoj domeni i na temelju njega odredimo položaj dominantnih polova zatvorenog sustava.
Dominantni polovi
Dominantni polovi su par konjugirano-kompleksnih polova koji su u s ravnini najbliži imaginarnoj osi i koji pretežno definiraju svojstva vođenog sustava. Da bi bili dominantni svi ostali se polovi trebaju nalaziti dovoljno daleko od dominantnih polova prema negativnom dijelu realne osi s ravnine. Dovoljno daleko znači da im realni dio bude po apsolutnoj vrijednosti najmanje 2 do 3 puta veći od realnog dijela dominantnih polova. Pri tome se treba paziti da ih ne pomaknemo previše lijevo, na primjer ne dalje od 5 realnih dijelova dominantnih polova. Optimalni izbor je 4 realna dijela dominantnog pola. Isto tako, ukoliko zatvoreni regulacijski sustav ima nula treba provjeriti da li su i one dovoljno lijevo od dominantnih polova kako ne bi utjecale na njih. Apsolutna vrijednost njegovog realnog djela bi također trebala biti 4 realna dijela dominantnih polova. Napišimo to pregledno:
Postupak odabira dominantnih polova za vođeni sustav k-tog reda:
a) Odabrati dva konjugirano kompleksna pola tako da vremenski odziv sustava drugog reda čiji su to polovi zadovoljava postavljene specifikacije.
b) Dodati (k-2) pola tako da im realni dijelovi budu apsolutno 4 puta veći od realnog dijela dominantnih polova.
Kako projektiramo diskretni regulator položaj polova trebamo prebaciti u z ravninu. O vezi s ravnine i z ravnine detaljno smo govorili u poglavlju 4.2.1 a u poglavlju 4.2.2 o položajima polova u s i z ravnini. Ovdje ćemo samo ukratko ponoviti osnovne zakonitosti. Slika 5.5.2 prikazuje vezu polova u s i z ravnini s ucrtanim osnovnim područjima unutar jedinične kružnice.
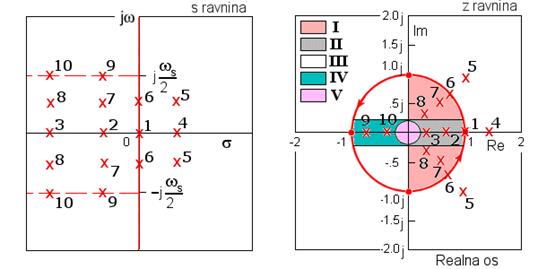
Slika 5.5.2. Preslikavanje polova iz s ravnine u z ravninu. Za opis karakterističnih područja I do V pogledati tekst
Na slici 5.5.2 označeno je pet karakterističnih područja. U području I odziv sustava je oscilatorno prigušen, u području II jako oscilatorno prigušen, u području III alternirajuće prigušen, u području IV jako alternirajuće prigušen dok postojanje pola u području V (u okolini ishodišta z ravnine) samo unosi kašnjenje ulaznog signala. Sjetimo li se priče o treptanju koje smo spomenuli još u poglavlju 5.2.2.1 alternirajući odziv zahtjeva nagle promjene upravljanja i veliko naprezanje sustava, pa polovi u III i IV području i nisu poželjni. Poželjna su područja I, II i V, ali i tu se polovi ne mogu postaviti baš u bilo kojem dijelu jediničnog polukruga. Ograničava nas zahtjev za odabir perioda uzorkovanja.
Kod definiranja željenog odziva obično brzinu odziva definiramo izborom vremena prvog maksimalnog prebačaja Tm ili izborom vremena porasta Tr. Vrijeme prvog maksimalnog prebačaja je vezano s frekvencijom prigušenih oscilacija izrazom Tm = π/ωp. Koordinata pola na imaginarnoj osi s ravnine predstavlja frekvenciju prigušenih oscilacija koje će zatvoreni sustav imati za baš taj dominantni pol. U poglavlju 2.2.6 o izboru frekvencije uzorkovanja kazali smo da period uzorkovanja treba biti 4 do 10 puta manji od vremena rasta Tr odnosno 8 do 20 puta manji od vremena maksimalnog prebačaja Tm. Uzmimo najmanju vrijednost: Tm =8T. Iz izraza koji povezuje i Tm i ωp slijedi ωp = π/8T, a kako je kružna frekvencija uzorkovanja ωs =2 π/T dobijemo zahtjev ωp = ωs /16, što znači da bi frekvencija prigušenih oscilacija ωp trebala biti bar 16 puta manja od frekvencije uzorkovanja ωs. Na slici 5.5.3 prikazan je dio osnovnog pojasa s ravnine koji zadovoljava ovaj uvjet i njemu pripadajući dio jedinične kružnice.
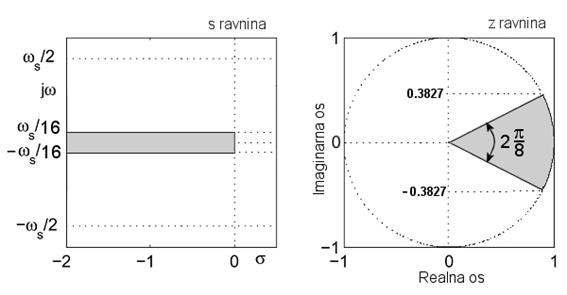
Slika 5.5.3. Preslikavanje dijela osnovnog pojasa s ravnine u z ravninu unutar kojega je period uzorkovanja bar 8 puta manji od vremena prvog maksimalnog prebačaja u vremenskom odzivu sustava
Kako bismo zadovoljili zahtjev odabira frekvencije uzorkovanja dominantni se polovi trebaju postaviti u kružnom isječku širine π/4. Pri tome jedinična kružnica odgovara imaginarnoj osi s ravnine, pa što je pol bliži jediničnoj kružnici to je njegov stupanj prigušenja manji, ali je taj pol ujedno i dominantniji. Pogledajmo primjer.
Primjer:
Sustav kojeg vodimo je trećeg reda prijenosne funkcije:
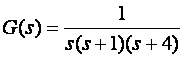
Želimo da stupanj prigušenja zatvorenog regulacijskog sustava bude z = 0.83 i frekvencija neprigušenih oscilacija ωn = 2.7 rad/s. Frekvencija prigušenih oscilacija je ωp = 1.5 rad/s. Iz z i ωn odredimo dominantne polove u s ravnini
![]()
koji će zadovoljavati jednadžbu:
![]()
Trebamo dodati i treći pol koji treba biti postavljen lijevo na realnoj osi. Odabiremo ga 4 puta dalje od realnog dijela dominantnih polova
![]()
Prebacimo sada ova tri pola u z ravninu. Najprije nam treba period uzimanja uzoraka. Kazali smo da ωs treba biti bar 16 puta veći od ωp, što znači da je granična vrijednost ωs = 16 ωp =24 rad/s, odnosno T treba biti kraći od 0.26 sek. Izabiremo T = 0.1 sek.

pa karakteristični polinom zatvorenog regulacijskog sustava u z području glasi:
![]()
U sljedećem ćemo poglavlju pokazati kako se na temelju ovog polinoma i poznavanja sustava koji se vodi proračunava matrica koeficijenata povratne veze varijabli stanja.
Prototipni sustav
Drugi način određivanja položaja polova zatvorene petlje je definiranje željenog odziva sustava na jedinični skok preko tkz. prototipnog sustava (eng. Prototype System) koji više nije drugog reda već općenito k-tog reda. Jedan od načina njegovog definiranja su normalizirani Besselovi polinomi k-tog reda Bk(s). Definira se prototipni sustav prijenosnom funkcijom:
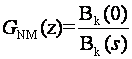 (5.5.7)
(5.5.7)
gdje je Bk(s) Besselov polinom k-tog reda. Prototipni sustav ima točno određeni odziv na jedinični skok bez prebačaja koji u određenom broju situacija zadovoljava. Besselovi polinomi se normaliziraju tako da vrijeme smirivanja na 1% vrijednost sustava definiranog prijenosnom funkcijom (5.5.7) bude 1 sekunda. U tom slučaju korijeni će imati vrijednosti prikazane u tablici na slici 5.5.4. Za bilo koje druge vrijednosti vremena smirivanja T1% i realni i imaginarni dio korijena se treba podijeliti sa tom željenom vrijednosti T1%.
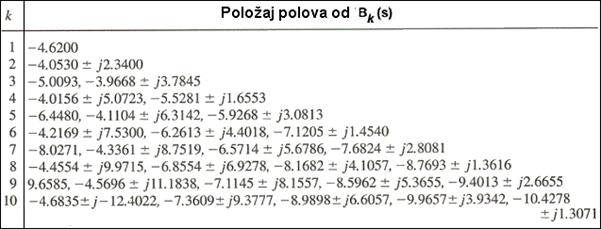
Slika 5.5.4. Normalizirani korijeni Besselovih polinoma k-tog reda za vrijeme smirivanja na 1% vrijednost 1 sekunda. Za bilo koje drugo vrijeme smirivanja T1% potrebno je i realni i imaginarni dio korijena podijeliti sa T1%
Normalizirane odzive sustava na jedinični skok prikazuje slika 5.5.5.
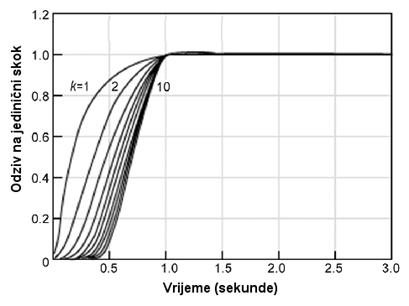
Slika 5.5.5. Odziv sustava prijenosne funkcije GNM(s)=Bk(0)/Bk(s) za korijene dane u tablici na slici 5.5.4
Postupak definiranja prototipnog sustava za vođeni sustav k-tog reda bi bio sljedeći:
a) Odredi željeno vrijeme smirivanja na 1% vrijednost T1%
b) Iz tablice izvadi korijene polinoma za k-ti red
c) Podijeli i realnu i imaginarnu vrijednost sa željenim T1%
d) Odredi period uzorkovanja za to
vrijeme smirivanja T1%
e) Prebaci polove u z područje i formiraj karakteristični polinom zatvorenog diskretnog regulacijskog sustava).
Pretpostavimo da je sustav kojeg vodimo isti onaj iz prethodnog primjera trećeg reda i da želimo vrijeme smirivanja na 1% vrijednost od 2 sekunde. Korijeni Besselovog polinoma trećeg reda nakon vremenske korekcije za vrijeme smirivanja su:
s1= -5.0093/2 = - 2.5047
s2= -3.9668/2 + j 3.7845/2 = -1.9834 + j 1.8922
s3= -3.9668/2 - j 3.7845/2 = -1.9834 - j 1.8922
a Besselov polinom B3(s) za tu vrijednost vremena smirivanja
![]()
Period uzimanja uzoraka treba biti manji od 0.33 sek. Izaberimo ponovo T = 0.1 sekundu, pa polovi u z području glase:
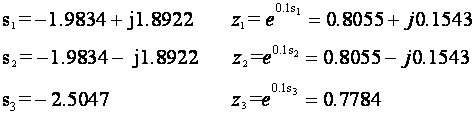
a karakteristični polinom zatvorenog regulacijskog sustava u z području glasi:
![]()
Naravno da Besselovi polinomi nisu jedini način definiranja prototipnog sustava. Prototipni sustav možemo definirati minimizirajući bilo koji od kriterija vremenske domene. Još 1953. D. Graham i R.C. Lathrop (D. Graham and R.C. Lathrop, “The synthesis of “optimum” transient response: criteria and standard forms”, AIEE Transactions, v. 72, pt. II, 273-288, 1953) su predložili korištenje minimizacije ITAE kriterija (integral apsolutne vremenski otežane pogreške):
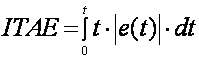 (5.5.8)
(5.5.8)
kod definiranja sustava s ‘optimalnim’ tranzijentnim karakteristikama. Postupak se može proširiti i na bilo koji integralni kriterij ili čak na minimizaciju bilo koje karakteristike vremenskog odziva sustava. Pogledajmo dva slučaja (R.A. Paz, Model Reference Design Technique, Klipsch School of Electrical and Computer Engineering, 2002):
a) definiranje prototipnog sustava koji minimizira ITAE kriterij, i
b) definiranje prototipnog sustava koji minimizira kriterij koji definiramo sumom vremena porasta od 10 do 90% konačne vrijednosti, vremena smirivanja na 5% vrijednosti i maksimalnog prebačaja
![]() (5.5.9)
(5.5.9)
Prototipni sustav definiramo prijenosnom funkcijom
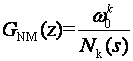 (5.5.10)
(5.5.10)
gdje je nazivnik Nk(s) oblika:
![]() (5.5.11)
(5.5.11)
Kružnu frekvenciju w0 nazivamo ‘prirodna frekvencija’ (eng. Natural Frequency) i koristimo kod prilagođavanja polinoma željenim karakteristikama vremenskog odziva.
Tablica na slici 5.5.6 daje vrijednosti polinoma za koji je minimiziran ITAE kriterij definiran jednadžbom (5.5.8).

Slika 5.5.6. Polinomi nazivnika prototipnog sustava koji minimiziraju ITAE kriterij
Osim ove tablice polinoma važna je i tablica koja povezuje osnovne specifikacije vremenskog odziva sustava (vremena porasta od 10 do 90% konačne vrijednosti, vremena smirivanja na 5% vrijednost i maksimalni prebačaj) s redom polinoma k i prirodnom frekvencijom w0. Prikazana je na slici 5.5.7.
|
k |
w0 T5% |
w0 Tr(10/90) |
M (%) |
|
2 |
3.137 |
2.296 |
2.76 |
|
3 |
3.648 |
2.365 |
1.57 |
|
4 |
4.188 |
2.428 |
1.90 |
|
5 |
4.732 |
2.487 |
1.79 |
|
6 |
5.254 |
2.532 |
1.97 |
Slika 5.5.7. Specifikacije vremenskog odziva povezane s redom polinoma prototipnog sustava k i prirodnom frekvencijom w0 za minimizaciju ITEA kriterija
Tablice na slikama 5.5.8 i 5.5.9 pokazuju to isto za minimizaciju kriterija definiranog izrazom (5.5.9):

Slika 5.5.8. Polinomi nazivnika prototipnog sustava koji minimiziraju kriterij J= Tr(10/90)+ T5% +200M
|
k |
w0 T5% |
w0 Tr(10/90) |
M (%) |
|
2 |
4.016 |
2.883 |
0.15 |
|
3 |
3.856 |
2.425 |
0.015 |
|
4 |
4.767 |
2.840 |
0.25 |
|
5 |
4.790 |
2.521 |
0.17 |
|
6 |
5.144 |
2.449 |
1.36 |
Slika 5.5.9. Specifikacije vremenskog odziva povezane s redom polinoma prototipnog sustava k i prirodnom frekvencijom w0 za minimizaciju J= Tr(10/90)+ T5% +200M
U drugom su slučaju prebačaji znatno manji, ali je zato vrijeme odziva duže.
Pogledajmo isti primjer kao i prije. Vođeni sustav je trećeg reda, a vrijeme smirivanja na 1% vrijednost treba biti 2 sekunde.
U tablici na slici 5.5.7 imamo specifikacije za minimizaciju ITEA kriterija i vrijeme smirivanja na 5%. Za sustav 3 reda ono iznosi 3.648/w0. Vrijeme smirivanja na 1% vrijednost će biti nešto duže. Uzeti ćemo vrijednost 4/w0. Iz jednadžbe 2=4/w0 izračunamo prirodnu frekvenciju w0=4/2=2, pa polinom trećeg reda iz tablice na slici 5.5.6 glasi:
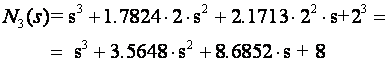
Korijeni polinoma su
S1= -1.07329 + j 2.11871
S2= -1.07329 - j 2.11871
S3= -1.41822
a u z području za T=0.1:
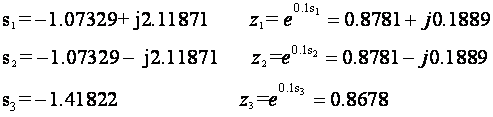
a karakteristični polinom zatvorenog regulacijskog sustava u z području glasi:
![]()
U tablici na slici 5.5.9 imamo specifikacije za minimizaciju složenog kriterija i vrijeme smirivanja na 5%. Za sustav 3 reda ono iznosi 3.856/w0. Uzet ćemo vrijednost 4/w0. Iz jednadžbe 2=4.23/w0 izračunamo prirodnu frekvenciju w0=4.23/2=2.115, pa polinom trećeg reda iz tablice na slici 5.5.8 glasi:
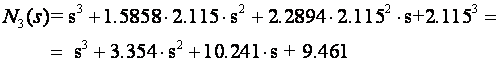
Korijeni polinoma su
s1= -1.05603 + j 2.55005
s2= -1.05603 - j 2.55005
s3= -1.24193
a u z području za T=0.1:
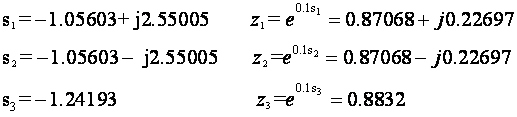
a karakteristični polinom zatvorenog regulacijskog sustava u z području glasi:
![]()
Slika 5.5.10 prikazuje odzive prototipnih sustava projektiranih po Besselovim polinomima, minimizaciji ITEA kriterija i minimizaciji složenog J kriterija.
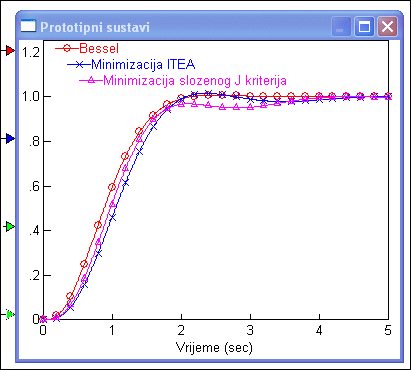
Slika 5.5.10. Odzivi prototipnih sustava projektiranih po Besselovim polinomima, minimizaciji ITEA kriterija i minimizaciji složenog J kriterija (prototype_systems.vsm).
Svi su odzivi vrlo slični uzme li se u obzir da smo vrijeme smirenja na 1% estimirali na temelju vremena smirenja n 5%.
'Dadbeat' vođenje
Posebno mjesto, bar s teorijske točke gledišta, ima vođenje kod kojega sve željene polove zatvorenog sustava smještamo u točku z=0. Takav je regulator poznat pod nazivom 'deadbeat' regulator koji smo za slučaj projektiranja vođenja na temelju impulsnih prijenosnih funkcija detaljno obradili u poglavlju 5.2.3.1 'Deadbeat' regulator. Istu ideju vođenja možemo primijeniti i kod vođenja povratnom vezom varijabli stanja. Pol u točki z=0 odgovara polu u s ravnini u točki -∞. Znamo da će odziv zatvorenog sustava biti brži ukoliko se polovi zatvorenog regulacijskog sustava pomaknu što više na lijevu stranu kompleksne s ravnine, odnosno u z ravnini približe što više ishodištu z ravnine. Granični slučaj je postavljanje svih polova zatvorenog regulacijskog sustava baš u točku z=0, što bi, ukoliko bi se uspjelo realizirati dalo najbrži mogući odziv bez prebačaja. Ovaj način vođenja poznat pod nazivom 'deadbeat' vođenje je unikatan za diskretno vođenje. Njega je nemoguće realizirati kontinuiranim vođenjem. Teorijski (uz neograničene vrijednosti upravljačkog signala) 'deatbeat' vođenje dovodi izlaz sustava u konačno stanje za onoliko diskretnih trenutaka vremena koliko prijenosna funkcija vođenog sustava ima više polova od nula i to uvijek, bez obzira u kojem je početnom stanju sustav bio. Rekli bismo idealno vođenje. Naravno u praksi to sve i nije tako idealno, o čemu smo već govorili u poglavlju 5.2.3.1 'Deadbeat' regulator. O specifičnosti projektiranja 'deadbeat' regulatora za vođenje povratnom vezom po varijablama stanja govorimo u poglavlju 5.5.1.7 'Deadbeat' vođenje povratnom vezom po varijablama stanja. Ovdje ćemo samo naglasiti da za 'deadbeat' vođenje karakteristični polinom zatvorenog regulacijskog sustava n-tog reda u z području glasi:
![]()
........................................................................
I na kraju naglasimo da je nedostatak projektiranja vođenja na temelju svih prototipnih sustava taj što se oni definiraju samo na temelju odziva sustava, minimizacijom pogreške e(t) ili njenih izvedenica. Kada se na temelju njega odredi matrica koeficijenata povratne veze varijabli stanja nema se nikakvog utjecaja na iznose upravljačkog signala. Zanimljivo bi bilo definirati prototipni sustav tako da se istovremeno minimizira i pogreška e(t) i iznosi upravljačkog signala u(t). Takav se način projektiranja regulatora povratnom vezom varijabli stanja naziva linearni kvadratni regulator (LQR – eng. Linear Quadratic Regulator) i spominjemo ga u poglavlju 5.5.5.