5.2.3.1. ‘Deadbeat’ regulator
‘Deadbeat’ regulator je regulator kod kojeg izlazna veličina u najmanjem broju diskretnih trenutaka dođe do svoje konačne vrijednosti. Koliko je to diskretnih trenutaka ovisi prije svega o samom sustavu koji se vodi i zahtjevima koje na regulator postavljamo. O njima smo govorili u prethodnom poglavlju, a samo ukratko ponovimo da se radi o zahtjevima stabilnosti, izvedivosti i potiskivanju pogrešaka ustaljenog stanja.
‘Deadbeat’ ponašanje je upravo ponašanje koje se u teoriji vođenja i priželjkuje. Idealno bi bilo kad bi izlazna veličina pratila ulaznu na način da do konačne vrijednosti dođe u istom trenu kada se promijenila ulazna veličina. Kako je to nemoguće zbog procesa uzorkovanja zadovoljavamo se i s tim da izlaz kasni samo jedan diskretni trenutak vremena. Važno je i to da odziv sustava nema prebačaja, već da se odmah smiri na konačnu vrijednost (bar u diskretnim trenucima uzorkovanja). Diskretno vođenje i ‘deadbeat’ dizajn to teorijski i dozvoljavaju, ali da sve nije toliko ružičasto koliko se na prvi pogled čini pokazati ćemo na kraju ovog poglavlja. Zadržimo se za sada samo na dobrim svojstvima ‘deadbeat’ regulatora.
Kao i kod većine postupaka projektiranja u diskretnom području krećemo od osnovne jednadžbe proračuna diskretnog regulatora
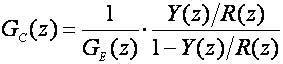(5.2.61)
Y(z)/R(z) zadajemo konačnim redom negativnih potencija varijable z:
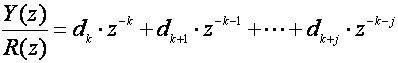(5.2.62)
Zahtjev za potiskivanjem pogreški ustaljenog stanja ograničava Y(z)/R(z) na oblik
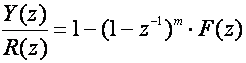(5.2.63)
gdje m ovisi o vrsti pogreške. Za pogrešku pomaka m=1, za pogrešku brzine m=2 i za pogrešku ubrzanja m=3. F(z) je polinom od negativnih potencija varijable z koji trebamo odrediti tako da daje oblik (5.2.26), ali da uz to zadovoljava još neka dodatna ograničenja.
U prethodnom smo poglavlju kazali da zahtjev izvedivosti ograničava potenciju k i kaže da ona mora biti najmanje jednaka razlici polova i nula impulsne prijenosne funkcije GE(z) sustava koji se vodi. 'Deadbeat' zahtjev traži da k bude upravo najmanji mogući, znači jednak razlici polova i nula funkcije GE(z). Tome se još treba dodati kašnjenje sustava koji se vodi iskazano kao cjelobrojni dio kvocijenta kašnjenja i perioda uzorkovanja M.
Pogledajmo ove zahtjeve za primjer sustava koji ima jedan pol više od nula i nema kašnjenja, te se zahtijeva da pogreška ustaljenog stanja pomaka bude jednaka 0. Kako sustav ima samo jedan pol više od nula, k treba biti najmanje jednak 1.
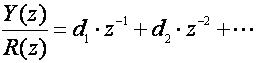(5.2.64)
Želimo li pogrešku ustaljenog stanja pomaka jednaku nuli m u jednadžbi (5.2.63) je jednak jedinici, pa je pišemo:
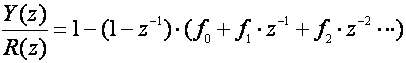(5.2.65)
Pomnožimo i izjednačimo (5.2.64) i (5.2.65):
Tražimo rješenje s najmanjim brojem članova. Očito je to
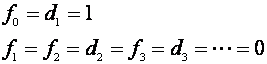
pa željena impulsna prijenosna funkcija vođenog sustava glasi
(5.2.66)
a polinom F(z) je jednak 1.
Impulsna prijenosna funkcija 'deadbeat' regulatora je:
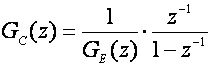(5.2.67)
Ima li sustav kašnjenje, i neka je cjelobrojni dio kvocijenta kašnjenja i perioda uzorkovanja jednak M, jednadžba (5.2.67) prelazi u oblik
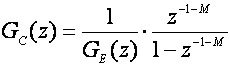(5.2.68)
Pogledajmo primjer:
Primjer:
Vratiti ćemo se našem primjeru egzotermičkog reaktora iz poglavlja o Dahlinovom regulatoru i aproksimaciji sustava modelom prvog reda s kašnjenjem:
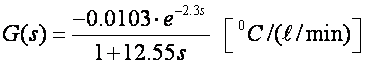
Za period uzorkovanja T=1, M=2 pa jednadžba regulatora glasi:
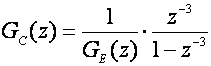
Ekvivalentna impulsna prijenosna funkcija vođenog sustava je:
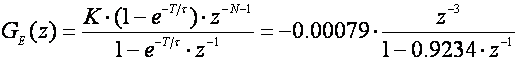
pa je impulsna prijenosna funkcija regulatora
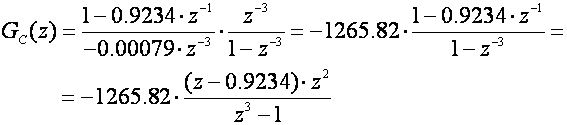
Slika 5.2.27 prikazuje odziv sustava vođenog 'deadbeat' regulatorom i pripadni upravljački signal za istu situaciju koju smo i prije analizirali - smanjenje referentne temperature sa 90 na 80oC.
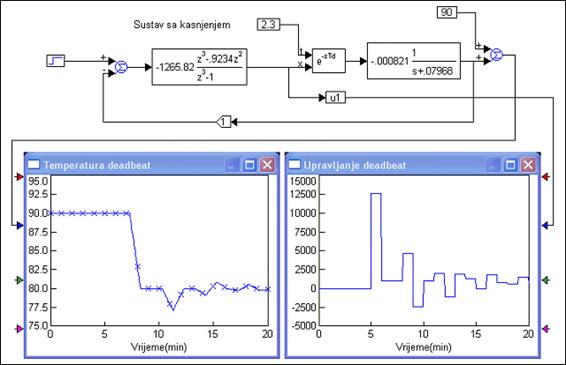
Slika 5.2.27. Egzotermički reaktor vođen 'deadbeat' regulatorom i njegov upravljački signal (sinteza-deadbeat.vsm)
Odziv vođenog sustava je trebao već nakon tri diskretna trenutka - perioda uzorkovanja (period uzorkovanja je 1 min, kašnjenje sustava je dva perioda uzorkovanja + jedan period uzorkovanja za koji želimo da sustav dođe u konačno stanje) doći do konačne vrijednosti ali očito da nije, već je dosta loš. Razlog lošeg rezultata je taj što je kašnjenje sustava 2.3, a regulator je projektiran tako da je uzet samo cjelobrojni dio ovog kašnjenja. Promijenimo li kašnjenje sustava na 2 situacija je bitno bolja i prikazuje je slika 5.2.28.
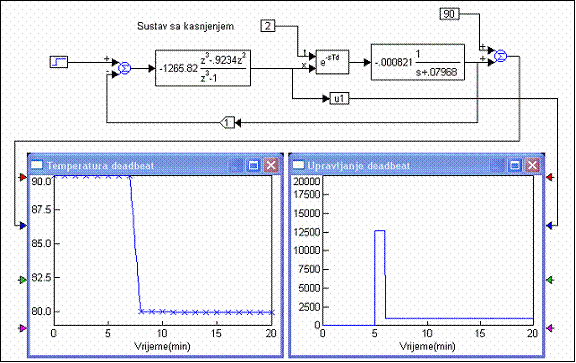
Slika 5.2.28. Egzotermički reaktor vođen 'deadbeat' regulatorom i njegov upravljački signal uz pretpostavku da je kašnjenje sustava 2 (sinteza-deadbeat.vsm)
Sada odziv točno nakon tri diskretna trenutka sa vrijednosti 90oC dođe do 80oC, ali to zahtijeva u prvom diskretnom trenutku protok vode za hlađenje od 12.500 l/min, što je naravno nelinearno i ne može se ostvariti. Simulacija nam daje idealni odziv koji se ne može praktično realizirati. U obzir bi trebali uzeti ograničenja upravljačkog signala, ali onda sustav više neće u tri diskretna trenutka doći do stacionarne vrijednosti.
Možemo zaključiti da je 'deadbeat' regulator jako osjetljiv na pogrešku modeliranja. Način njegovog djelovanja je takav da regulator poništi sve polove i nule sustava, te impulsnoj prijenosnoj funkciji zatvorenog sustava doda višestruki pol u točki z=0. Mala greška u modeliranju sustava koji se vodi (koja je uvijek prisutna) daje veliku grešku u rezultatu vođenja.
Prisjetimo li se preslikavanja s ravnine u z ravninu, pol u točki z=0 odgovara polu na realnoj osi s ravnine u minus beskonačno.
Kontinuirani regulator s polom u beskonačnosti se ne može izvesti, a u diskretnom području postaviti pol u točku z=0 je potpuno izvedivo, bar teorijski. To je jedna od prednosti diskretne izvedbe regulatora, međutim pogledamo li upravljački signal lako ćemo uočiti drugi problem. 'Deadbeat' regulator zahtijeva u jednom diskretnom trenutku vremena veliku skokovitu promjenu upravljačke veličine koju najčešće nije moguće realno napraviti, a ukoliko postoji pogreška modeliranja onda još k tome zahtijeva alternirajuću promjenu signala upravljanja. Sjetimo li se diskusije o treptanju, razlog je taj što rezultantni ekvivalentni pol zbog pogreške modeliranja padne na lijevu stranu realne z osi.
Zbog toga je 'deadbeat' regulator zanimljiv više s teorijske točke gledanja, nego s praktične. Na vrijednost upravljačkog signala se u biti može utjecati kroz izbor broja diskretnih trenutaka vremena u kojima želimo da izlaz sustava dođe do konačne vrijednosti i izbor perioda uzorkovanja. Međutim kako je po definiciji pravi 'deadbeat' regulator onaj koji u minimalnom broju diskretnih trenutaka vremena dođe do konačne vrijednosti, a to je vezano isključivo s razlikom u broju polova i nula vođenog sustava, jedini nezavisni parametar u projektiranju je period uzorkovanja, pa ga treba pažljivo odabirati (ne zaboravite da o periodu uzorkovanja preko GE(z) ovisi i impulsna prijenosna funkcija regulatora).
Drugi praktični pristup 'deadbeat' vođenju je korištenje 'mekše' verzije dodavanjem dodatnog pola u željeni odziv sustava u točki z=c. Konstanta c je naravno manja od jedinice kako pol ne bi izašao iz jedinične kružnice i naziva se prigušujući težinski faktor (eng. Staleness Weighting Factor). Uz ovaj prigušni član jednadžba (5.2.63) se mijenja u oblik
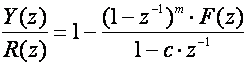(5.2.69)
Primjer:
Za prethodni slučaj korigirajmo regulator za težinski faktor c=0.5 i c=0.6.
I dalje želimo samo pogrešku ustaljenog stanja pomaka jednaku 0, pa je m=1. Najniži mogući polinom F(z)=1
(Napomena: Pokazati ćemo postupak projektiranja kod kojega se kašnjenje sustava dodaje željenoj prijenosnoj funkciji tek na kraju):
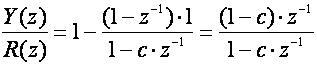
Sada dodajemo kašnjenje od dvije diskretne jedinice pa željena impulsna prijenosna funkcija zatvorenog sustava treba glasiti:
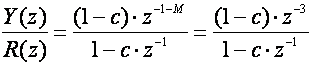
Uvrstimo je u jednadžbu regulatora:
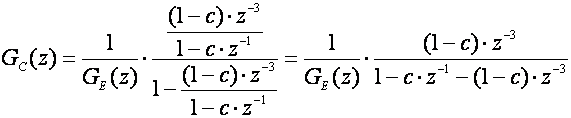
Za
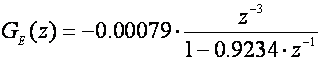
rezultat je:
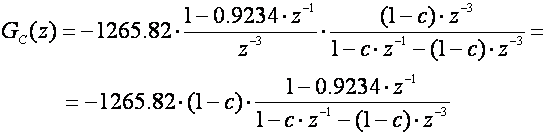
Za c=0.5 imamo:
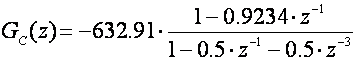
a za c=0.6:
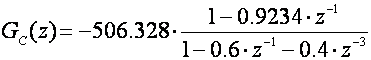
Odzive prikazuje slika 5.2.29 u usporedbi s prethodnim rezultatom.
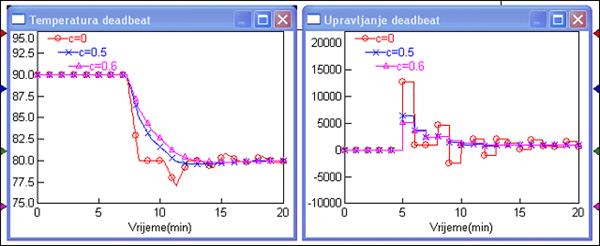
Slika 5.2.29. Egzotermički reaktor vođen 'deadbeat' regulatorom i njegov upravljački signal za slučaj neprigušenja i prigušenja regulatora (c=0.5 i c=0.6) (sinteza-deadbeat_2.vsm)
Rezultati su uočljivi. Odziv više nije toliko brz, ali mu zato pogreška krivog modeliranja kašnjenja sustava više ne smeta, a i upravljački signal je puno prihvatljiviji. Što je c veći to je odziv sporiji, ali i upravljački signal manji i manjih promjena.