5.2.3.2. Kalmanov algoritam
Kalman je 1954. godine (R.E. Kalman, diskusija na članak A.R. Bergen, J.R. Ragazzini, Sampled-Data Processing Technique for Feedback Control Systems, Trans. AIEE, Nov. 1954, pp. 236-247) predložio algoritam s konačnim vremenom dolaska izlazne veličine do krajnje vrijednosti, kod kojeg se postavljaju ograničenja na promjenu upravljačke veličine. Polazna jednadžba je ponovo jednadžba za proračun diskretnog regulatora:
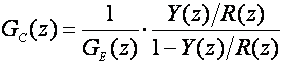 (5.2.61)
(5.2.61)
Željeni odziv zatvorenog regulacijskog sustava na pobudu jediničnog skoka Kalman zadaje u diskretnom području definirajući željeni slijed promjene izlaznog signala i željeni slijed promjene upravljačkog signala. Pri tome, broj diskretnih trenutaka u kojima će izlazna veličina doći do konačne vrijednosti nije potpuno proizvoljan. I ovdje vrijede ograničenja izvedivosti koja smo prije spominjali. Prevedemo li ih na zahtjeve Kalmanovog algoritma, broj diskretnih trenutaka vremena u kojima izlazna veličina može doći do konačne vrijednosti treba biti najmanje jednak razlici broja polova i nula sustava koji se vodi.
Kalmanov postupak ćemo ilustrirati na primjeru dolaska do konačne vrijednosti izlazne veličine u dva diskretna trenutka vremena. Slika 5.2.30 prikazuje slijed izlaznog signala i njemu pridruženog upravljačkog signala.
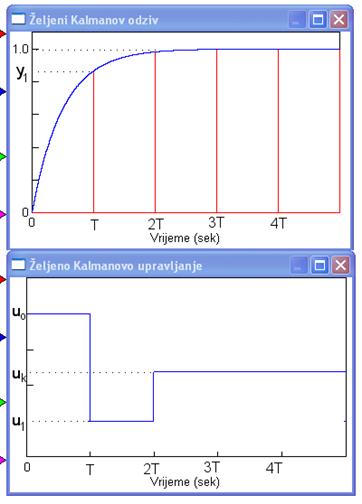
Slika 5.2.30. Željeni slijed izlaznog i upravljačkog signala
Izlazni i upravljački signal možemo pisati u obliku beskonačnog reda negativnih potencija varijable z:
![]() (5.2.70)
(5.2.70)
![]() (5.2.71)
(5.2.71)
Ulazni, referentni signal je jedinični skok kojeg u z području prikazujemo izrazom:
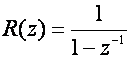 (5.2.72)
(5.2.72)
Uvedimo dvije razlomljene racionalne funkcije i definirajmo ih kvocijentima
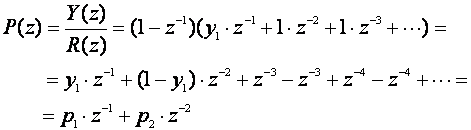 (5.2.73)
(5.2.73)
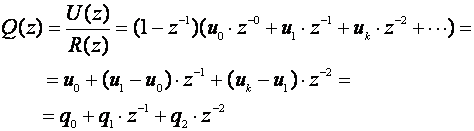 (5.2.74)
(5.2.74)
Podijelimo P(z) sa Q(z):
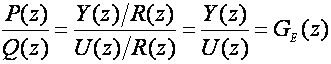 (5.2.75)
(5.2.75)
i sve uvrstimo u jednadžbu (5.2.61):
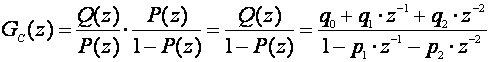 (5.2.76)
(5.2.76)
gdje su:
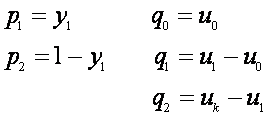 (5.2.77)
(5.2.77)
koeficijenti koje određujemo iz ekvivalentne impulsne prijenosne funkcije sustava koji se vodi
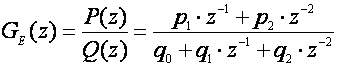 (5.2.78)
(5.2.78)
jednostavnom usporedbom koeficijenata uz iste potencije brojnika i nazivnika.
Pri tome prema (5.2.77) treba vrijediti:
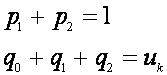 (5.2.79)
(5.2.79)
Napomena: Ukoliko nije ispunjen zahtjev p1+p2=1 ekvivalentnu impulsnu prijenosnu funkciju sustava koji se vodi treba najprije dovesti u oblik kod kojeg je to ispunjeno. Na primjer neka je
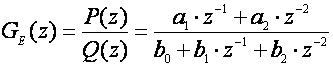 (5.2.80)
(5.2.80)
i neka
![]() .
.
Ukoliko podijelimo brojnik i nazivnik sa sumom (a1+a2) ništa se neće promijeniti, a zahtjev će biti ispunjen:
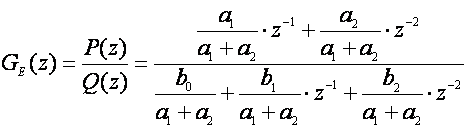 (5.2.81)
(5.2.81)
i vrijedi:
 (5.2.82)
(5.2.82)
Isto tako vrijedi:
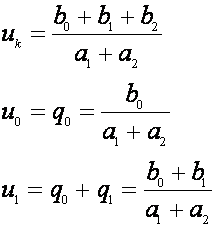 (5.2.83)
(5.2.83)
Treba naglasiti da su ovo vrijednosti regulatora za skokovitu ulaznu pobudu. Ukoliko sustav ima vremensko kašnjenje L, tada se željeni odziv treba pomaknuti na cijeli dio kvocijenta kašnjenja i perioda uzorkovanja M=cijeli dio(L/T).
- sustav prvog reda s kašnjenjem
- sustav drugog reda s kašnjenjem