Vođeni sustav aproksimiramo prijenosnom funkcijom prvog reda s kašnjenjem
Kazali smo da je to jedan od standardnih načina modeliranja sustava koji se vodi i da su ga koristili još Ziegler-Nichols kod podešavanja PID regulatora metodom reakcijske krivulje. Prijenosna funkcija sustava koji se vodi je oblika:
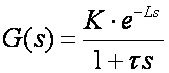(5.2.84)
a impulsna prijenosna funkcija ekvivalentnog sustava:
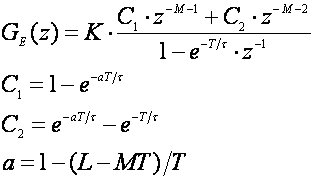(5.2.85)
Nije ispunjen uvjet p1+p2=1 pa trebamo primijeniti normiranje (pojačanje sustava Km prebacujemo u nazivnik). Prema (5.2.80) i (5.2.82) uz dodavanje kašnjenja N polinomu P(z) koji sada glasi:
(5.2.86)
dobijemo:
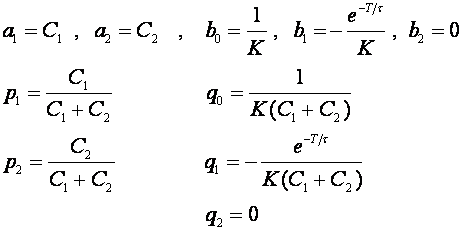(5.2.87)
Impulsna prijenosna funkcija regulatora se dobije uvrštavanjem ovih vrijednosti u (5.2.76):
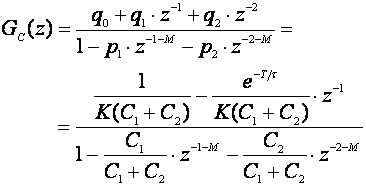(5.2.88)
Primjer:
Ponovo egzotermički reaktor aproksimiran matematičkim modelom:
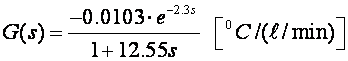
L=2.3 pa je N=2 i a=0.7. Pojačanje K=-0.0103 i τ=12.55. Za T=1 imamo:
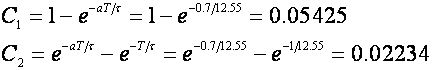
pa su koeficijenti:
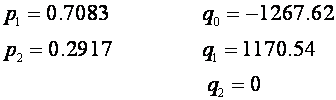
i impulsna prijenosna funkcija regulatora
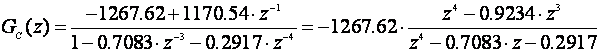
Odziv prikazuje slika 5.2.31.
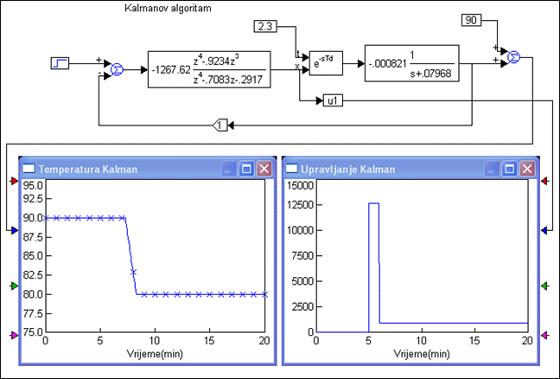
Slika 5.2.31. Egzotermički reaktor vođen Kalmanovim regulatorom i njegov upravljački signal za sustav prvog reda s kašnjenjem (sinteza-Kalman.vsm)
Skoro pa idealni odziv. Regulator smo projektirali uz zahtjev da izlaz u dva diskretna trenutka dođe do konačne vrijednosti, a on je došao već za jedan diskretni trenutak, naravno nakon kašnjenja. I upravljački signal s početne vrijednosti u0 odmah skače na konačnu uk. Nema međuvrijednosti u1 - razlog je taj što se radi o sustavu prvog reda za koga je b2 =0.