Vođeni sustav aproksimiramo prijenosnom funkcijom drugog reda s kašnjenjem
Sustav drugog reda s kašnjenjem drugi je oblik tipičnog modela kojim modeliramo realne sustave:
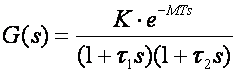(5.2.89)
najprije ga prebacimo u diskretno područje u oblik ekvivalentne impulsne prijenosne funkcije:
(5.2.90)
I ovdje trebamo primijeniti normiranje brojnika i uključiti kašnjenje, te usporediti koeficijente uz istu potenciju jednadžbe (5.2.89) i (5.2.78). Rezultat je:
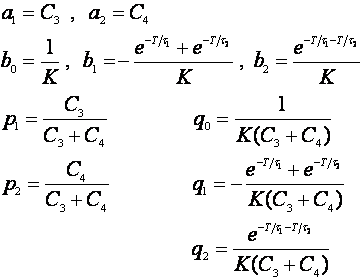(5.2.91)
a impulsna prijenosna funkcija regulatora:
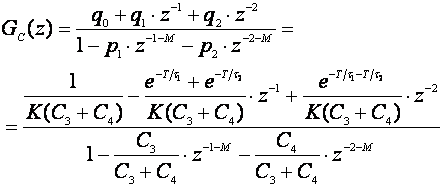(5.2.92)
Primjer:
Ponovo egzotermički proces i model oblika
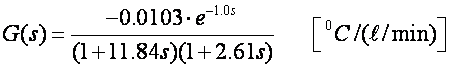
Imamo K=-0.0103 , L=1, τ1=11.84 , τ2=2.61. Za T=1, M=1 koeficijenti su:
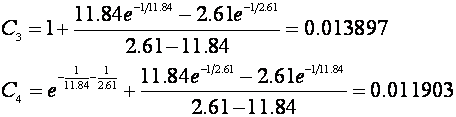
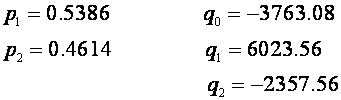
i impulsna prijenosna funkcija regulatora
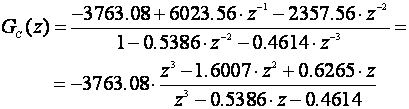
Odziv prikazuje slika 5.2.32.
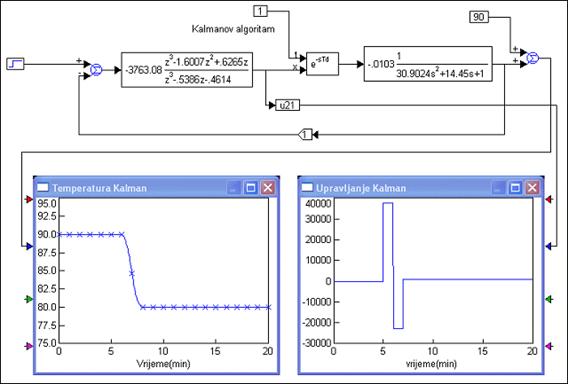
Slika 5.2.32. Egzotermički reaktor vođen Kalmanovim regulatorom i njegov upravljački signal za sustav drugog reda s kašnjenjem (sinteza-Kalman2.vsm)
Dobili smo upravo ono što smo i htjeli. Izlazni signal u dva diskretna trenutka pada s vrijednosti 90oC na 80oC, a pri tome se i upravljački signal mijenja samo dva puta prije nego poprimi konačnu vrijednost.
Problem u primjeni Kalmanovog algoritma je zahtjev za velikim i naglim promjenama upravljačkog signala unutar nekoliko diskretnih trenutaka. Pri tome opet možemo uočiti da se u drugom diskretnom trenutku zahtjeva smanjenje upravljanja (protoka) za više od 20.000 l/min u odnosu na vrijednost u stacionarnom stanju za temperaturu 90oC. To je sigurno neizvedivo zato što stacionarna vrijednost protoka za 90oC sigurno nije 20.000 l/min. Nerealan i je i zahtjev da se protok u prvom diskretnom trenutku vremena poveća za skoro 40.000 l/min.
Objasnimo ga na primjeru vožnje automobila. Želimo od nekog početnog položaja doći do konačnog u najkraćem vremenu. Kako ćemo to izvesti? Tako da ćemo u prvom trenutku maksimalno pritisnuti gas (upravljačka veličina maksimalno pozitivna). Automobil će ubrzavati najvećim mogućim ubrzanjem zato što mu je kao ciljna brzina (koju treba postići za pritisnutu papučicu gasa do kraja) postavljena najveća moguća brzina koju on može dosegnuti. Nakon toga u pravilno izabranom trenutku skinemo potpuno nogu s gasa i maksimalno pritisnemo kočnicu (upravljačka veličina maksimalno negativna). Automobil će se početi usporavati najvećom mogućom deceleracijom. Ukoliko smo odabrali pravi trenutak prelaska s maksimalno pozitivne na maksimalno negativnu vrijednost automobil će se zaustaviti točno na mjestu na kojem smo željeli doći. Zakasnimo li na pravi trenutak promjene upravljačke veličine (alterniranja) imati ćemo prebačaj željenog položaja, a ukoliko uranimo imati ćemo podbačaj.
Kalmanov regulator upravo to i radi, samo što se ne upravlja vremenom alterniranja, već amplitudom pozitivnog i negativnog signala. U prvom je diskretnom trenutku veliko pozitivno upravljanje, a u drugom negativno. Pravilno odabrane amplitude daju najbrži mogući dolazak izlazne veličine od početne do krajnje vrijednosti.
Problem je jedino taj što je takvo upravljanje obično realno neizvodivo. Rješenje je postavljanje ograničenja na veličinu promjene upravljačkog signala uklanjanjem polova koji uvjetuju njegovu alternirajuću promjenu. O tome smo detaljno govorili u poglavlju o treptanju upravljačkog signala kod Dahlina. Alternirajućeg upravljačkog signala se rješavamo tako da polove koji su na negativnom dijelu realne osi zamjenjujemo vrijednošću z=1. U slučaju Kalmanovog regulatora polove regulatora definira nazivnik:
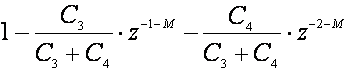(5.2.93)
Označimo kvocijent C4/(C3+C4) s p i pretpostavimo da je M=1 kao u našem slučaju. Nazivnik sada možemo pisati:
(5.2.94)
Sustav ima tri pola. Jedan u točki z=1 i dva pola koja imaju negativni realni dio. Očito je problem u njima pa u drugom faktoru zamijenimo z s 1 i dobijemo:
(5.2.95)
To je oblik kojim zamijenimo nazivnik impulsne prijenosne funkcije regulatora. Za neki drugi M nazivnik se zamijeni izrazom:
(5.2.96)
pa impulsna prijenosna funkcija regulatora glasi:
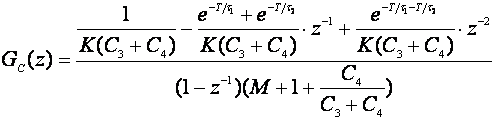(5.2.97)
Primjer:
Primijenimo korekciju treptanja upravljačkog signala na prethodni primjer:
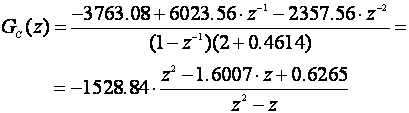
Slika 5.2.33 prikazuje usporedne odzive sustava vođenog Kalmanovim regulatorom s i bez korekcije treptanja.
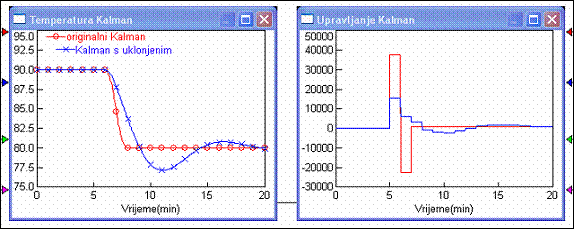
Slika 5.2.33. Rezultati primjene Kalmanovog regulatora kod kojeg je ispravljena pojava treptanja za λ=0.5 (sinteza-Kalman3.vsm)
Upravljački signal je ublažen, a odziv istina u tri diskretna trenutka, ne računajući kašnjenje dođe do konačne vrijednosti, ali je i prebaci pa imamo prigušene oscilacije.