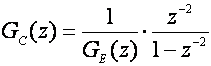5.2.3. Postupak temeljen na definiranju željenog odziva zatvorenog regulacijskog sustava u diskretnim trenucima vremena
I ovaj postupak ima istu polaznu jednadžbu kojom definiramo impulsnu prijenosnu funkciju regulatora u ovisnosti o impulsnoj prijenosnoj funkciji ekvivalentnog sustava koji se vodi i željenoj impulsnoj prijenosnoj funkciji zatvorenog sustava
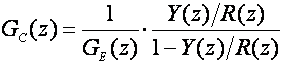 (5.2.52)
(5.2.52)
Razlika je jedino u tome što Y(z)/R(z) direktno definiramo u z području i vežemo s odzivom sustava u diskretnim trenucima vremena. Kako se zahtijeva da odziv sustava u konačnom broju diskretnih trenutaka dođe do stacionarne vrijednosti postupak je poznat po nazivu vođenje s konačnim vremenom smirivanja (eng. Finite Settling Time Control). Ukoliko se do stacionarne vrijednosti dođe u najmanjem mogućem broju diskretnih koraka regulator se zove 'deadbeat' regulator i njega posebno analiziramo u sljedećem poglavlju.
Proračun impulsne prijenosne funkcije regulatora po jednadžbi (5.2.52) ne može biti potpuno proizvoljan. Postoje određena ograničenja i zahtjevi koje moramo ispuniti.
Dva osnovna zahtjeva su da diskretni regulator bude takav da vođeni sustav bude stabilan, a da regulator bude izvediv.
Uvjet stabilnosti povlači zahtjev da se impulsnom prijenosnom funkcijom regulatora GC(z) ne smiju poništavati nestabilne nule sustava koje su izvan jedinične kružnice. Uvijek postoji pogreška modeliranja , pa nule nikada nisu točno tamo gdje smo proračunali da se one nalaze. Pretpostavimo da je nula sustava u točki n koja je izvan jedinične kružnice i da je pogreška modeliranja ε. Impulsna prijenosna funkcija regulatora glasi:
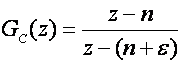 (5.2.53)
(5.2.53)
što nakon povratka u diskretno vremensko područje daje:
![]() (5.2.54)
(5.2.54)
Izraz postaje beskonačan kada k teži u beskonačno bez obzira koliko je mala pogreška modeliranja ε, što kao posljedicu ima i beskonačnu vrijednost upravljačkog signala i na kraju nestabilni sustav.
Uvjet izvedivosti postavlja ograničenja i na izbor Y(z)/R(z). Red brojnika impulsne prijenosne funkcije regulatora ne može biti veći od reda nazivnika, pa na primjer u slučaju da je vođeni sustav GE(z) drugog reda bez nula ne može zahtijevati da željeni odziv Y(z)/R(z) bude prvog reda. Rezultat bi bio regulator samo s jednom nulom što je fizički neizvedivo. Pogledajmo ovu situaciju još općenitije.
Podijelimo li brojnik i nazivnik željenog odziva Y(z)/R(z) u općem slučaju dobijemo slijed
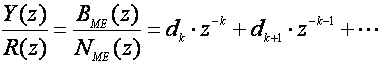 (5.2.55)
(5.2.55)
gdje je k razlika između broja polova i broja nula željenog odziva. Na sličan način možemo prikazati i impulsnu prijenosnu funkciju sustava koji se vodi
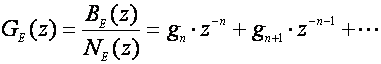 (5.2.56)
(5.2.56)
Uvrstimo li oba izraza u (5.2.52) dobijemo:
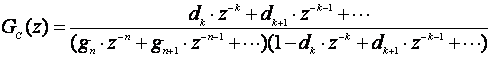 (5.2.57)
(5.2.57)
Da bi regulator bio izvediv k treba biti veći ili jednak od n.
Uvjetu izvedivosti vratiti ćemo se ponovo nakon analize ograničenja koja na izbor Y(z)/R(z) može postaviti zahtjev za eliminiranjem pogreški ustaljenog stanja.
Pogreška se u z području računa izrazom
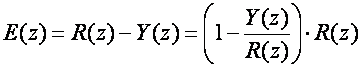 (5.2.58)
(5.2.58)
Pogreške ustaljenog stanja ovise o dovedenoj pobudi koja je u općem slučaju u z području oblika:
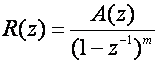 (5.2.59)
(5.2.59)
A(z) je polinom varijable z koji ovisi o vrsti pobude. Za skokovitu pobudu (pogreška ustaljenog stanja pomaka) koeficijent m = 1 i A(z) = 1. Za jediničnu pravčastu uzlaznu pobudu (pogreška ustaljenog stanja brzine) m = 2 , a A(z) = Tz-1 itd.
Pogreška ustaljenog stanja m-tog reda biti će eliminirana ukoliko se Y(z)/R(z) izabere u obliku:
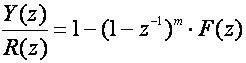 (5.2.60)
(5.2.60)
gdje je F(z) polinom od varijable z.
Vratimo se sada ponovo na uvjet izvedivosti. Komentirajući impulsnu prijenosnu funkciju regulatora (5.2.57) kazali smo da treba biti k ≥ n. To određuje i ograničava izbor polinoma F(z).
Primjer:
Uzmimo za primjer da imamo sustav koji ima dva pola više nego što ima nula i da su mu svi polovi i nule unutar jedinične kružnice. Želimo projektirati regulator koji uklanja pogrešku ustaljenog stanja pomaka (m = 1).
Ako impulsna prijenosna funkcija sustava ima dva pola više od broja nula očito za nju vrijedi da je u jednadžbi (5.2.56) n=1, a kako k mora biti najmanje jednak vrijednosti n, željenu impulsnu prijenosnu funkciju vođenog sustava prikazanu u obliku (5.2.55) možemo pisati:
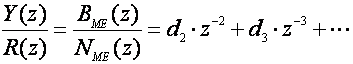
Napišimo i F(z) u obliku polinoma varijable z:
![]()
Za nultu pogrešku ustaljenog stanja pomaka (m=1) u skladu s (5.2.60) treba vrijediti:
![]()
Nakon množenja dobijemo:
![]()
Izjednačavajući koeficijente lijeve i desne strane lako je ustanoviti da jednadžbu možemo zadovoljiti za sljedeći odabir koeficijenata:
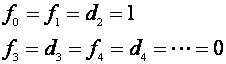
odnosno
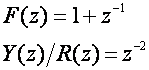
pa je moguće rješenje zadatka (regulator izvediv i pogreška ustaljenog stanja pomaka će biti jednaka nuli), impulsna prijenosna funkcija regulatora: