5.5.1.2. Određivanje matrice povratne veze varijabli stanja – jednoveličinski sustav
Nakon što
smo odredili željeni položaj
polova prijenosne funkcije zatvorene petlje p1, p2, ...,
pn, ostaje nam još proračunati matricu
povratne veze varijabli stanja K. Određujemo je iz uvjeta da
baš ti polovi budu vlastite vrijednosti matrice
.
(5.5.12)
Postupak rješavanja je direktan i jednostavan. Polazna jednadžba je:
Rješavanjem determinante i izjednačavanjem koeficijenata uz iste potencije varijable z formira se skup n algebarskih jednadžbi iz kojih se izračunaju koeficijenti povratne veze varijabli stanja. Pogledajmo primjer:
Ilustrirajmo postupak jednostavnim sustavom drugog reda s jednom ulaznom varijablom opisanog jednadžbama varijabli stanja:
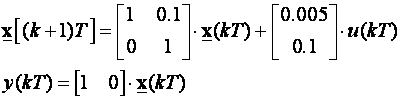
T=0.01, a željena karakteristična jednadžba vođenog sustava treba biti
Riješimo determinantu:
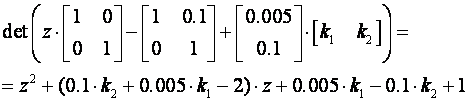
Izjednačavanjem koeficijenata uz iste potencije varijable z dobijemo sustav od dvije jednadžbe s dvije nepoznanice:
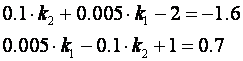
koje je lako riješiti, pa su koeficijenti povratne veze varijabli stanja:
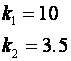
Slika 5.5.11 Prikazuje odziv vođenog sustava na pobudnu funkciju jediničnog skoka.
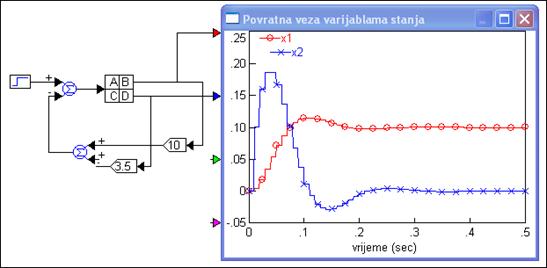
Slika 5.5.11. Odziv vođenog sustava (varijable_stanja_povratna_1.vsm)
Napomena: Uočite da u odzivu postoji i pogreška ustaljenog stanja položaja (na ulazu smo imali jedinični skok, a varijabla x1 koja odgovara izlazu sustava se ustali na vrijednost od 0.1). Taj problem, koji se inače javlja kod vođenja povratnom vezom varijabli stanja diskutiramo malo kasnije pri kraju ovog poglavlja.
U slučaju složenijeg sustava s više varijabli stanja proračun postaje zahtjevan, pa je postojanje dobrog CAD alata nužno. Spomenuli smo dva takva primjera: komercijalni Matlab i besplatni Octave ili Scilab s kojim se može napraviti više manje sve kao i u Matlabu (za više detalja o programima Octave i Scilab pogledajte naš 'download dio'. Sva tri programa u Control Toolboxu imaju gotove funkcije za proračun povratne veze varijabli stanja. U Matlabu i Octaveu čak se i isto nazivaju 'place' , ali im je sintaksa različita, pa ćemo razliku pokazati na gornjem primjeru. Sintaksa Scilaba je skoro ista kao i sintaksa Matlaba samo što se funkcija zove 'ppol'.
>> Fi=[1 0.1;0 1]
Fi =
1.0000 0.1000
0 1.0000
>> Psi=[0.005;0.1]
Psi =
0.0050
0.1000
>> z1=0.8+0.2449j
z1 =
0.8000 + 0.2449i
>> polinom=[z1;conj(z1)]
polinom =
0.8000 + 0.2449i
0.8000 - 0.2449i
>> K=place(Fi, Psi, polinom)
K =
9.9976 3.5001
Primjena programa Scilab u proračunu koeficijenata povratne veze varijabli stanja
-->Fi =[1 0.1;0 1]
Fi =
! 1. .1 !
! 0. 1. !
-->Psi =[0.005;0.1]
Psi =
! .005 !
! .1 !
-->c=[1 0]
c =
! 1. 0. !
-->z1=0.8+0.2449*%i //Ovo je način definiranja kompleksnog broja
u programu Scilab
z1 =
.8 + .2449i
-->korijeni=[z1,conj(z1)]
korijeni =
! .8 + .2449i .8 - .2449i !
-->K=ppol(Fi,Psi,korijeni)
K =
! 9.997601 3.5001199 !
Primjena programa Octave u proračunu koeficijenata povratne veze varijabli stanja
>> Fi =[1 0.1;0 1]
Fi =
1.00000 0.10000
0.00000 1.00000
>> Psi =[0.005;0.1]
Psi =
0.00500
0.10000
>> c=[1 0]
c =
1 0
>> sys=ss2sys(Fi, Psi,c,[],0.01)
sys =
{
Fi =
1.00000 0.10000
0.00000 1.00000
Psi =
0.00500
0.10000
c =
1 0
d = 0
inname =
(
[1] = u_1
)
n = 0
nz = 2
outname =
(
[1] = y_1
)
stname =
(
[1] = xd_1
[2] = xd_2
)
sys =
2 0 0 1
tsam = 0.010000
yd = 1
}
>> z1=0.8+0.2449j
z1 = 0.80000 + 0.24490i
>> korijeni=[z1,conj(z1)]
polinom =
0.80000 + 0.24490i 0.80000 - 0.24490i
>> K=place(sys,korijeni)
K =
9.99760 3.50012
Naravno da su rezultati više manje slični. Treba se primijetiti da se kod programa Octave najprije treba definirati opis sustava varijablama stanja, pa tek onda računati koeficijente. Za detalje o primjeni programima Octave i Scilab pogledajte naš 'download dio'.
Na FESB-u je u okviru Centra za znanstveno računanje Sveučilišta u Splitu instalirana i on-line verzija programa Octave OCTAVE ON-LINE. Gornji smo primjer prenijeli u prozor ovog on-line programa, pa ga možete odmah i isprobati, a možete mijenjati i vrijednosti parametara:
Spomenimo još i to da se funkcija 'place' u Octaveu može koristiti samo za sustave s jednim ulazom i jednim izlazom, dok se u Matlabu može koristiti i za viševeličinske sustave.
U Matlabu postoji i funkcija 'acker' koja se temelji na tzv. Ackermannovoj formuli pomoću koje se matrica K direktno proračunava. Ackermanova formula je značajna s teorijske točke gledanja, ali računski dosta složena zato što zahtijeva invertiranje matrice upravljivosti WC. Ovdje ćemo je navesti bez izvoda (za detaljni izvod pogledati K.J. Astrom, B. Wittenmark, Computer-Controlled Systems, Prentice- Hall, 1990):
(5.5.14)
gdje su:
- matrice upravljivosti (vidi
poglavlje 4.7.3 Upravljivost i dohvatljivost)
- karakteristični polinom željenog, vođenog sustava u
kojem smo varijablu z zamijenili matricom sustava
.
Za prethodni primjer imamo:
U Matlabu je sintaksa funkcije acker ista kao i sintaksa funkcije place:
>> K= acker(Fi, Psi, polinom)
K =
9.9976 3.5001
ali ima ograničenje da se može primijeniti samo na sustave s jednim ulazom i jednim izlazom (SISO sustavi).
Vratimo se sada ponovo na naš primjer i promijenimo željeni položaj polova zatvorenog sustava. Neka je nova željena karakteristična jednadžba
pa su jednadžbe za proračun regulatora:
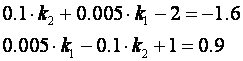
Novo rješenje je
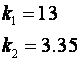
Slika 5.5.12 pokazuje usporedbu između odziva varijable stanja x1 za oba slučaja.
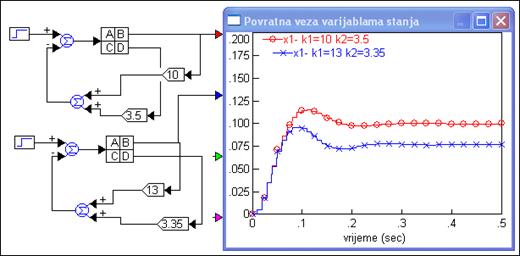
Slika 5.5.12. Usporedba odziva varijable stanja x1 za različite vrijednosti koeficijenata povratne veze varijabli stanja (varijable_stanja_povratna_2.vsm)
Važno je primijetiti da se nisu promijenile samo dinamičke karakteristike odziva već i konačna vrijednost na koju se varijabla stanja x1 smiruje. Postoji pogreška ustaljenog stanja (na ulazu smo imali jedinični skok) koja je različita za različite vrijednosti koeficijenata. Razlika neće postojati jedino onda ukoliko je ulazna, referentna veličina jednaka nuli (r=0). Na primjer slika 5.5.13 prikazuje odzive varijabli stanja x1 za različite vrijednosti koeficijenata povratne veze varijabli stanja i početni uvjet x1(0)=0.1.
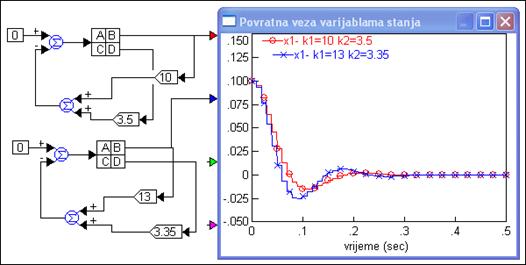
Slika 5.5.13. Usporedba odziva varijable stanja x1 za različite vrijednosti koeficijenata povratne veze varijabli stanja, ulazni signal jednak nuli i početni uvjet x1(0)=0.1 (varijable_stanja_povratna_3.vsm)
Povratnom vezom varijabli stanja prvenstveno djelujemo na dinamička svojstava sustava, a ukoliko želimo da vođeni sustav i na zadovoljavajući način prati ulaznu veličinu bez pogreški ustaljenog stanja (slijedno vođenje – eng. Tracking Control) regulacijski sustav trebamo doraditi. O tome govorimo u poglavlju 5.5.1.4, ali prije toga osvrnimo se ukratko na probleme koje donosi postojanje više upravljačkih ulaza.