4.7.3. Upravljivost i dohvatljivost
Ova dva pojma, zajedno s pojmom osmotrivosti temeljni su pojmovi opisa sustava varijablama stanja. Upravljivost i dohvatljivost se odnose na pitanje može li se sustav iz početnog stanja dovesti u konačno stanje vanjskom pobudom, dok se osmotrivost odnosi na pitanje može li se odrediti stanje sustava na temelju promatranja ulaza i izlaza. Pitanja je postavio i na njih odgovore dao 1960. godine R.E. Kalman.
Ponovo krećemo od jednadžbi varijabli stanja
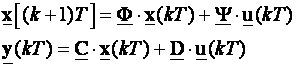(4.7.1)
Pretpostavljamo da se sustav nalazi u početnom stanju
i da je n-tog reda. Rješenje jednadžbe u k-tom trenutku
vremena je
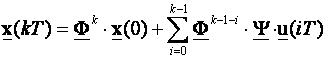(4.7.20)
a u n-tom trenutku vremena (n odgovara redu sustava) jednadžbu (4.7.20) možemo pisati:
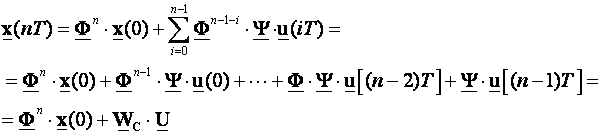(4.7.21)
gdje su
Ukoliko WC ima rang n, moguće je pronaći n jednadžbi pomoću kojih se može proračunati signal vođenja koji će sustav iz početnog stanja dovesti u konačno stanje. Rješenje nije jedinstveno ukoliko sustav ima više ulaza. Na temelju toga možemo kazati:
Sustav je upravljiv (eng. Controllable) ukoliko se može pronaći slijed upravljačkih signala pomoću kojih se može doći u ishodište prostora stanja iz bilo kojeg početnog stanja u konačnom broju koraka.
Sustav je dohvatljiv (eng. Reachable) ukoliko se može pronaći slijed upravljačkih signala pomoću kojih se može doći u bilo koje stanje iz bilo kojeg početnog stanja u konačnom broju koraka.
Upravljivost ne uključuje
dohvatljivost što se može vidjeti iz jednadžbe (4.7.21). Ukoliko je
u ishodište prostora stanja može se doći s nultim ulazom,
što ne znači da će sustav bit i dohvatljiv.
Ipak ova dva pojma su
ekvivalentna ukoliko se matrica sustava
može invertirati.
Matematički dohvatljivost analiziramo tako da provjeravamo rang matrice WC .
Sustav je dohvatljiv onda i samo onda kada matrica WC ima rang n.
Primjer:
Da li je sustav opisan jednadžbama varijabli stanja
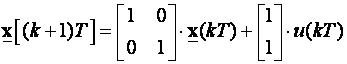
dohvatljiv?
Formiramo matricu WC. Sustav je drugog reda:
Matrica ima rang 1 zato što je
pa sustav nije dohvatljiv
Dohvatljivost i upravljivost
možemo objasniti na način da karakteristična jednadžba
ima korijen koji se nakon množenja
s matricom 
, kojom definiramo utjecaje ulaza na stanja sustava
poništi, te se ulaznim signalima ne može djelovati na sva stanja sustava.
Prema Cayley – Hamiltonovom teoremu sva stanja koja se mogu dohvatiti iz ishodišta prostora stanja određena su stupcima matrice WC. Matematički to znači da sva dohvatljiva stanja pripadaju linearnom podprostoru čiju bazu čine stupci matrice WC.
Primjer:
Za sustav zadan jednadžbama
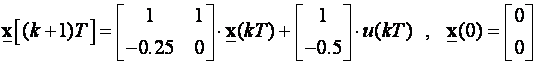
odredi koja su stanja dostupna iz ishodišta prostora stanja?
Formiramo matricu WC:
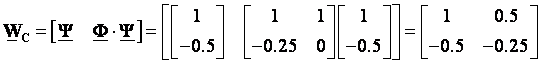
Matrica WC
ima rang 1, sustav je nedohvatljiv. Postoji samo ograničeni broj stanja do
kojih se može doći iz ishodišta. Definira ih vektorski podprostor definiran
stupcima matrica WC koji su linearno zavisni
vektori. Prema tome vektorski podprostor dohvatljivih stanja određen je
vektorom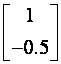 
. Iz ishodišta je moguće dohvatiti samo ona stanja koja su
linearna kombinacija tog vektora.
Kao primjer odrediti ćemo
sekvencu koja sustav iz ishodišta dovodi u drugom diskretnom trenutku (k=2)
u stanje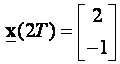 
.
Prema (4.7.21) pišemo
Kako je
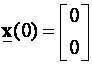dalje slijedi
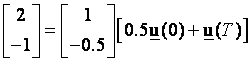
što daje dvije linearno zavisne jednadžbe
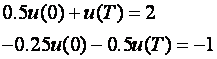
Množenjem donje jednadžbe s -2 dobijemo gornju jednadžbu. Zbog toga je sustav rješiv iako je determinanta sustava jednaka 0.
Jedna od upravljačkih sekvenci je u(0)=2 i u(1)=1.
Slika 4.7.3 to na neki način ilustrira. Sustavi su identični. Prvi ima na ulazu skokoviti signal amplitude 2, a početni uvjeti su 0, 0. Sustav će već u trenutku T=0.1 doći u vrijednosti u stanja 2 i -1. Druga slika pokazuje što se dogodi ukoliko u početnim stanjima 2 i -1 priključimo ulazni signal amplitude 1. Sustav će stalno ostati u stanju u kojem se zatekao, a to je ono što smo i tražili.
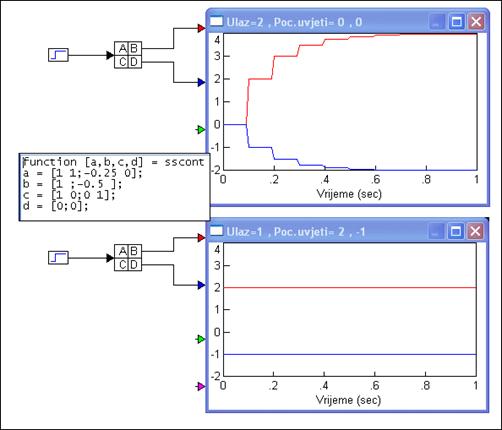
Slika 4.7.3. Ilustracija primjera vremenskim odzivima T=0.1 (varijable_stanja_dohvatljivost.vsm)
Želimo li isti taj sustav
dovesti u stanje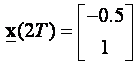 
dobijemo
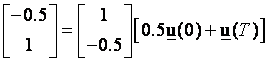
što daje dvije linearno nezavisne jednadžbe
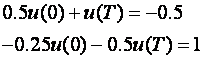
pa je sustav nerješiv,
sekvenca se ne može pronaći. Razlog je taj što
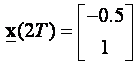ne pripada vektorskom podprostoru definiranom stupcima
matrice WC .
Zanimljivo je da se sustav
ipak može dovesti u to stanje, ali jedino ukoliko ima točne određene početne
uvjete. Ukoliko je na primjer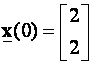 
prema (4.7.21) imamo:
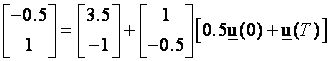
što ponovo daje dvije linearno zavisne jednadžbe
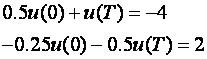
pa se upravljačka sekvenca može pronaći. Jedna od mogućih je u(0)=-2 i u(1)=-3.