Digitalno vođenje on-line (FESB, Split)

4.7.4. Osmotrivost

Cilj: Naučiti pojam osmotrivosti vrlo važan u modernoj teoriji vođenja

Zanima nas određivanje stanja sustava na temelju promatranja izlaza sustava. Sustav je osmotriv (eng. Observable) ukoliko mjerenjem izlaznih veličina y možemo u potpunosti odrediti sva stanja sustava x. Prije matematičke analize osmotrivosti uvedimo i suprotan pojam. Kažimo kada će neko od stanja sustava biti neosmotrivo.

Stanje sustava x⁰ ≠ 0 je neosmotrivo ukoliko postoji konačan k₁ ≥ n-1 takav da je y(kT) = 0 za 0 ≤ k ≤ k₁ kada je x(0) = x⁰ i u(kT) = 0 za 0 ≤ k ≤ k₁.

Diskretni sustav

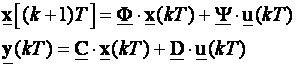(4.7.1)

je osmotriv ukoliko postoji konačni k takav da je znanje ulazne sekvence u(0), u(T), ..., u[(k-1)T] i izlazne sekvence y(0), y(T), ..., y[(k-1)T] dovoljno da se odredi početno stanje sustava.

Pretpostavka da je ulazna sekvenca u(kT) = 0 ne utječe na matematički izvod, ali pojednostavljuje postupak. Pišemo:

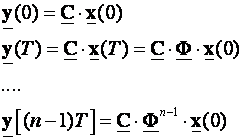(4.7.22)

što vektorski možemo napisati

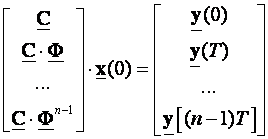(4.7.23)

Označimo s W_O matricu na lijevoj strani

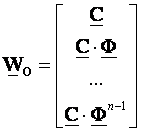
i nazovimo je matrica osmotrivosti. Stanje x(0) je prema (4.7.23) osmotrivo samo ukoliko matrica W_O ima rang n, iz čega slijedi i osnovni teorem osmotrivosti:

Sustav je osmotriv ukoliko matrica osmotrivosti W_O ima rang n.

Neosmotriva stanja formiraju nul prostor matrice W_O što drugim riječima znači da sva neosmotriva stanja u jednadžbi izlaza daju nule.

Primjer:

Da li je sustav opisan jednadžbama:

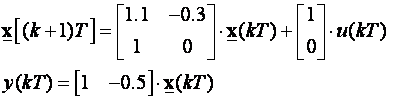
osmotriv?

Matrica osmotrivosti je

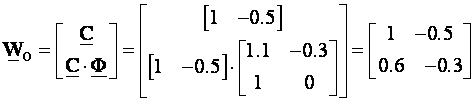
i ima rang 1 što znači da je sustav neosmotriv.

Neosmotriva stanja su ona koja u jednadžbi

daju nule. Primjer je stanje 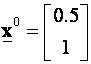i sve njegove linearne kombinacije. Npr. za početno stanje odziv je jednak nuli (na slici 4.7.4 gornja dva odziva).

Za ostala početna stanja odzivi će biti različiti od nule, ali je moguće pronaći cijeli niz početnih stanja za koje će odzivi biti identični. Sva su ta stanja paralelna i udaljena za . Na primjer u drugom redu slike 4.7.4 dan je slobodni odziv za početno stanje . Isti odziv imati će i stanje 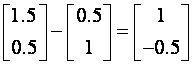. Slično na donjoj slici je slobodni odziv za početno stanje 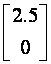. Isti će odziv bit i za stanje 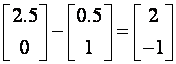itd.

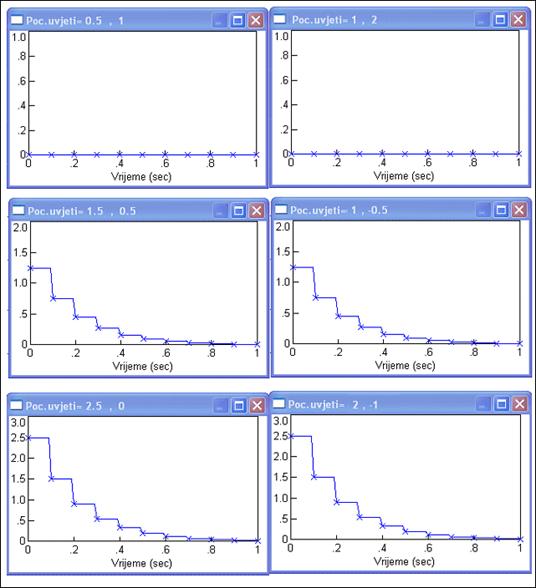
Slika 4.7.4. Slobodni odzivi sustava iz primjera za različite početne uvjete

S ovim završavamo kratki pregled analize diskretnih sustava i u sljedećem poglavlju prikazujemo osnovne postupke sinteze. Dajemo odgovor na pitanje – kako proračunati diskretni regulator da zatvoreni regulacijski sustav zadovoljava određene specifikacije. Za razumijevanje teksta nužno je pročitati i dodatak s definicijama.