5.5.1.4. Slijedno vođenje povratnom vezom varijabli stanja
U poglavlju 5.5.1.2 smo spomenuli da stacionarna vrijednost varijabli stanja na ne-nulti ulaz ovisi o vrijednostima koeficijenata povratne veze varijabli stanja. Koeficijentima povratne veze varijabli stanja utječemo na dinamičke karakteristike odziva, ali ukoliko želimo imati i zadovoljavajuće praćenje ulazne veličine, sustav vođenja trebamo doraditi. U slučaju sustava s jednim ulazom i jednim izlazom to je relativno jednostavno, pa ćemo cijeli postupak detaljno objasniti. Za projektiranje slijednog vođenja sustava s više ulaza i izlaza čitatelje upućujemo na literaturu (na primjer R.J. Vaccaro, Digital Control – A State-Space Approach, McGraw Hill, 1995).
Krećemo od jednadžbi stanja sustava koji se vodi uz pretpostavku da je izlazna veličina jednaka prvoj varijabli stanja x1(kT):
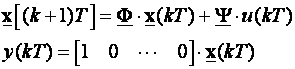(5.5.16)
Iz vektora koeficijenata povratne veze varijabli stanja izdvojimo prvi element a na njegovo mjesto u matrici koeficijenata povratne veze varijabli stanja stavljamo 0 i označavamo je s K2:
(5.5.17)
Koeficijent k1 prebacimo iza sumatora pa dobijemo situaciju koju zorno prikazuje slika 5.5.15.
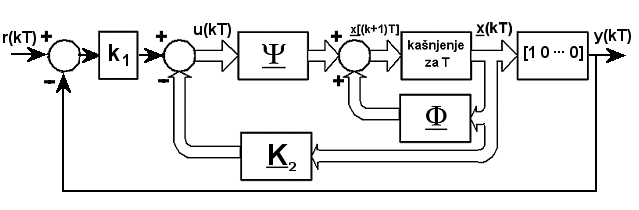
Slika 5.5.15. Slijedno vođenje za sustave s jednim ulazom i jednim izlazom
Upravljački signal je sada jednak:
(5.5.18)
Nakon množenja koeficijent k1 ponovo vraćamo u matricu povratne veze varijabli stanja K:
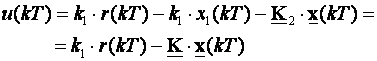(5.5.19)
Uvrstimo dobiveni rezultat u (5.5.16):
(5.5.20)
Kako se koeficijenti povratne veze varijabli stanja biraju tako da sustav bude stabilan (svi korijeni karakterističnog polinoma vođenog sustava su unutar jedinične kružnice), vođeni sustav će doći u stacionarno stanje xS. Možemo ga proračunati tako da stavimo r(kT)=1 i x[(k+1)T] = x(kT) (u stacionarnom stanju vrijednosti varijabli stanja se ne mijenjaju):
(5.5.21)
Riješimo jednadžbu po xS:
(5.5.22)
Matrica u zagradi se može invertirati zato što (F - Y·K) ima vlastite vrijednosti unutar jedinične kružnice, pa je rješenje jednadžbe (5.5.22) jedinstveno. Stacionarna vrijednost izlazne veličine yS je:
(5.5.23)
Zanima nas u kojim uvjetima će vrijediti yS = 0 (nema pogreške ustaljenog stanja pomaka, sustav u ustaljenom stanju idealno prati skokovitu referentnu veličinu). To će biti ispunjeno samo onda kada matrica F bude imala vlastitu (karakterističnu) vrijednost jednaku jedinici (l1=1). U tom je slučaju produkt matrice F i vlastitog (karakterističnog) vektora e1 = [1 0 ··· 0]T, koji pripada toj vlastitoj vrijednosti, jednak samom vektoru:
(5.5.24)
Pokažimo najprije da je e1 zadovoljava jednadžbu (5.5.21):
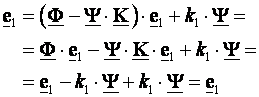(5.5.25)
Isto tako imamo:
(5.5.26)
Uvrštavanjem xS= e1 dobijemo:
(5.5.27)
Zaključak je da vođeni sustav nema pogrešku ustaljenog stanja pomaka (idealno prati ulaznu skokovitu promjenu) samo ukoliko je sam sustav koji se vodi ne-nulte vrsti, što znači da ima bar jedan pol u točki z = 1 (odnosno s=0). To smo uostalom utvrdili i u poglavlju 4.3. Sustav ne-nulte vrsti je sustav integracijskog tipa. Nazivamo ga i sustav bez izjednačenja. Ovdje je važno uočiti da se pogreška ustaljenog stanja ne može eliminirati određenom kombinacijom vrijednosti koeficijenata povratne veze ustaljenog stanja. Promijeniti će se njena vrijednost, ali je vođeni sustav neće imati samo ukoliko u direktnoj grani postoji čisti integracijski dio (dio s polom u točki z=1).
Ukoliko integracijskog dijela nema ostaje nam samo to da u direktnu granu (prije prvog sumatora) unesemo dodatno pojačanje KR. Novu regulacijsku shemu pokazuje slika 5.5.16:
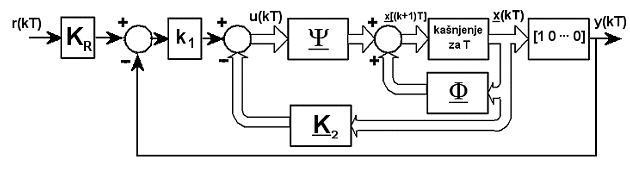
Slika 5.5.16. Dodavanje korekcijskog pojačanja u direktnu granu u slučaju da sustav nema niti jedan pol u točki z=1
Dodatno pojačanje KR treba biti jednako recipročnoj vrijednosti stacionarne vrijednosti yS koja se računa jednadžbom (5.5.23):
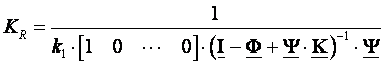(5.5.28)
i očito je ovisna o vrijednostima koeficijenata povratne veze varijabli stanja. Promijenimo li koeficijente, trebamo promijeniti i vrijednost ovog pojačanja.
Za primjer jednoveličinskog sustava koji smo već spominjali opisanog diskretnim jednadžbama varijabli stanja:
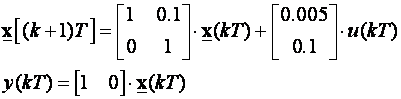
koeficijente povratne veze varijabli stanja za željeni karakteristični polinom:
smo već izračunali. Vrijednosti su im:
Izlazna veličina je prva varijabla stanja, pa izvlačimo k1 = 10 i formiramo novu matricu koeficijenata povratne veze varijabli stanja:
Iz matrice F odmah uočavamo da vođeni sustav ima čak dva pola u točki z=1 (sustav je dvostruki integrator), pa se pogreška ustaljenog stanja može eliminirati samo prelaskom na regulacijsku shemu sa slike 5.5.15. Pojačanje KR nam ne treba (KR=1). Slika 5.5.17 prikazuje usporedbu odziva vođenog sustava za standardnu shemu vođenja povratnom vezom varijabli stanja i modificiranu shemu prilagođenu slijednom vođenju.
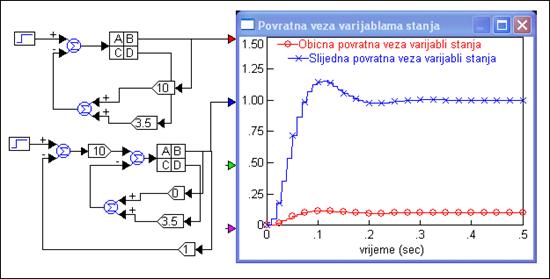
Slika 5.5.17. Usporedba odziva vođenog sustava za standardnu shemu vođenja povratnom vezom varijabli stanja i modificiranu shemu prilagođenu slijednom vođenju (varijable_stanja_slijedno_1.vsm)
U shemi slijednog vođenja smo iz pedagoških razloga ostavili granu povratne veze varijabli stanja s vrijednosti pojačanja 0. Naravno da je u stvarnoj realizaciji neće biti, već će se regulacijski sustav prikazivati shemom sa slike 5.5.18.
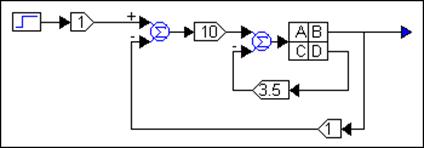
Slika 5.5.18. Slijedno vođenje povratnom vezom varijabli stanja
Da je sustav bio bez polova u točki z=1, vrijednost pojačanja prije prvog sumatora bi bila različita od 1.
Napomena: Blokovskom manipulacijom se može pokazati da je slijedni sustav temeljen na povratnoj vezi varijablama stanja za sustav drugog reda, ekvivalentan klasičnom serijskom regulatoru PD tipa s pred-filtrom prvog reda u grani referentne veličine prije sumatora. Isto tako za sustav trećeg reda ekvivalentna shema slijednom vođenju temeljenom na povratnoj vezi varijabli stanja je serijski PID regulator s pred-filtrom drugog reda u grani referentne veličine prije sumatora. Pokušajte za vježbu to izvesti.