5.5.1.5. Slijedno vođenje povratnom vezom varijabli stanja - druga rješenja
Regulacijsku shemu nešto izmijenjenog pristupa slijednom vođenju povratnom vezom varijabli stanja prikazuje slika 5.5.19.
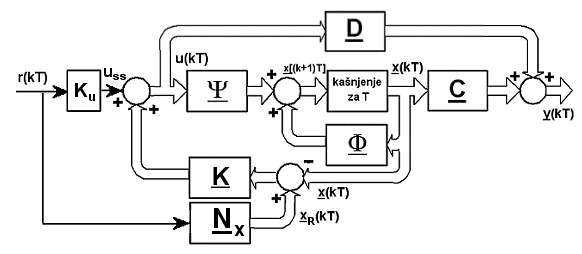
Slika 5.5.19. Općenitija shema slijednog vođenja temeljenog na povratnoj vezi varijabli stanja
Ukoliko je sustav koji se vodi integracijskog tipa pojačanje Ku je jednako 0, pa se referentni signal dovodi samo u obliku referentnih stanja xR.
Upravljački signal je u ovom slučaju:
(5.5.29)
U stacionarnom stanju imamo
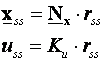(5.5.30)
a ukoliko je diskretni opis sustava koji se vodi
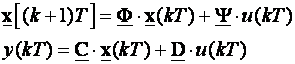(5.5.31)
jednadžbe sustava u stacionarnom stanju možemo napisati:
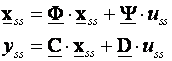(5.5.32)
Jednadžba (5.5.32) u matričnom obliku glasi:
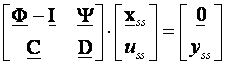(5.5.33)
Kombiniranjem (5.5.33) s (5.5.30) uz ySS=rSS dobijemo:
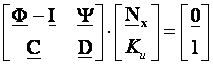(5.5.34)
iz čega slijedi izraz za proračun matrice Kx i pojačanja Ku :
(5.5.35)
Za prethodni primjer
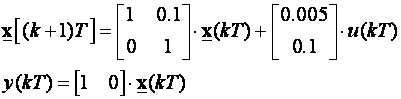
projektirajmo drugi tip slijednog vođenja. Sustav ima dva integracijska elementa pa je za očekivati da vrijednost pojačanja Ku bude jednaka 0.
Pišemo matričnu jednadžbu oblika (5.5.35):
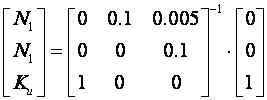
Rješenje je
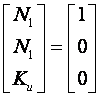
što je u biti isti rezultat koji smo imali u prethodnom poglavlju.
........................................................
Napomena: Do rezultata smo isto došli jednostavno u nekoliko koraka korištenjem programa Octave:
>> Matr=[0 0.1 0.005;0 0 0.1;1 0 0]
Matr =
0 0.1000 0.0050
0 0 0.1000
1.0000 0 0
>> Matr1=[0;0;1]
Matr1 =
0
0
1
>> Nxu=Matr\Matr1
Nxu =
1
0
0
........................................................
Pogledajmo i primjer sustava koji nema integracijskih članova:
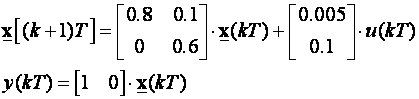
Pojačanja računamo jednadžbom
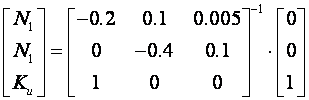
a rješenje je:
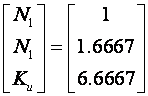
Kako se promijenio model sustava koji se vodi trebamo proračunati i novu povratnu vezu varijabli stanja. Za isti karakteristični polinom
rezultat je
Slika 5.5.20 prikazuje odziv ovog tipa slijednog sustava u usporedbi sa standardnim vođenjem temeljenim na povratnoj vezi varijabli stanja.
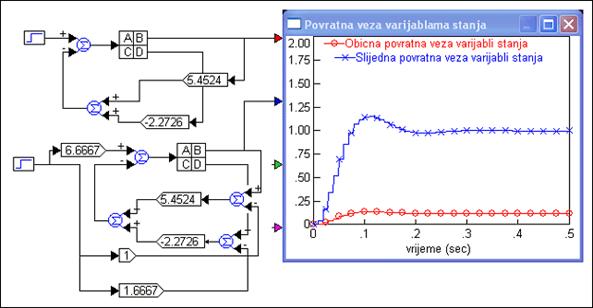
Slika 5.5.20. Odziv drugog tipa slijednog sustava u usporedbi sa standardnim vođenjem temeljenim na povratnoj vezi varijabli stanja (varijable_stanja_slijedno_2.vsm)