5.5.1.6. Slijedno vođenje povratnom vezom varijabli stanja s integratorom u direktnoj grani
Dodavanje novog integracijskog člana u direktnu (serijsku) granu u matematičkom opisu sustava varijablama stanja znači dodavanje nove jednadžbe varijabli stanja čija je jednadžba:
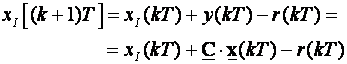(5.5.36)
Novi opis sustava s ovom dodanom varijablom stanja koja pripada čistom integracijskom članu je:
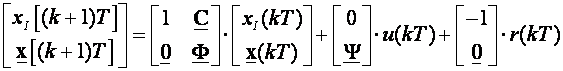(5.5.37)
Sustav vođenja prikazuje slika 5.5.21.
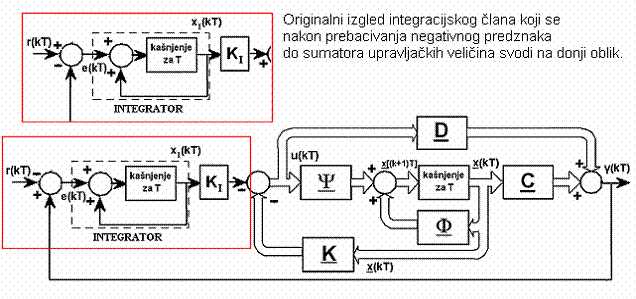
Slika 5.5.21. Slijedno vođenje s integratorom u direktnoj grani
Obratite pažnju na to da smo negativni predznak vanjske povratne veze po izlazu prebacili do sumatora na kojem se upravljački signali zbrajaju tako da je jednadžba (5.5.36) integracijskog člana točna, a ukupni upravljački signal je jednak:
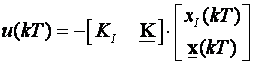(5.5.38)
Koeficijenti povratne veze varijabli stanja kojima je dodano i pojačanje integracijskog člana računaju se na uobičajeni način – usporedbom karakterističnog polinoma vođenog sustava sa željenim karakterističnim polinomom ili primjenom Ackermannove formule (vidi poglavlje 5.5.1.2). Razlika je jedino u tome što su matrice varijabli stanja sada definirane jednadžbom (5.5.37).
Pogledajmo primjer sustava koji nije integracijskog tipa (nema polove u točki z=1) za T=0.01:
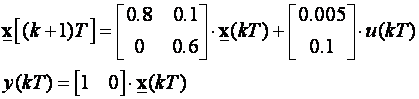
Za karakteristični polinom oblika
vrijednosti koeficijenata povratne veze varijabli stanja smo već izračunali i iznose:
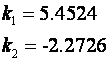
Odziv sustava je prikazan na slici 5.5.22 u usporedbi sa sustavom kojem smo u serijskoj grani dodali integrator. Sustav s integratorom sada ima tri jednadžbe varijabli stanja:
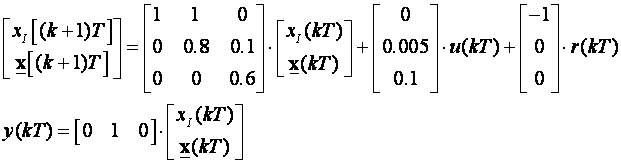
Željenoj karakterističnoj jednadžbi vođenog sustava trebamo dodati još jedan pol koji postavljamo tako da ne utječe na dinamička svojstva dominantnih polova. Stavljamo ga u točku z = 0.1 pa željeni karakteristični polinom vođenog sustava glasi:
Sada rješavamo determinantu:
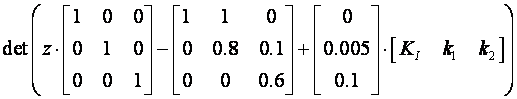
i izjednačimo je sa željenim karakterističnim polinomom.
Rezultat je
Prvi koeficijent je KI =7.49828 a druga dva su koeficijenti povratne veze varijabli stanja k1 = 18.4077 k2 = 6.0796.
Slika 5.5.22 prikazuje odziv vođenog sustava u usporedbi sa standardnim vođenjem povratnom vezom varijabli stanja bez integracijskog člana u serijskoj grani.
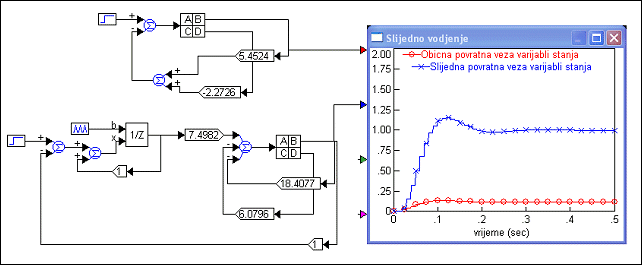
Slika 5.5.22. Odziv vođenog sustava u usporedbi sa standardnim vođenjem povratnom vezom varijabli stanja bez integracijskog člana u serijskoj grani (varijable_stanja_slijedno_3.vsm)
Napomenimo da je moguće kombinirati ovaj postupak slijednog vođenja s integratorom u direktnoj grani i postupak iz prethodnog poglavlja s unaprijednom matricom Nx s kojom se množi referentni signal.