5.5.1.6. 'Deadbeat' vođenje povratnom vezom po varijablama stanja
Željeni karakteristični polinom zatvorenog regulacijskog sustava n-tog reda za 'deadbeat' vođenje je
(5.5.38-1)
što znači da sve polove zatvorenog regulacijskog sustava želimo postaviti u ishodište z ravnine. Prisjetimo se, pol u ishodištu z ravnine odgovara polu u -¥ s ravnine, što daje najveću moguću brzinu odziva vođenog sustava. Ovakvo je vođenje u stvari ono čemu težimo, a unikatno je i može se (bar teorijski) realizirati samo diskretnim vođenjem. O projektiranju 'deadbeat' regulatora na temelju impulsne prijenosne funkcija sustava koji se vodi, detaljno smo govorili u poglavlju 5.2.3.1 'Deadbeat' regulator. Ovdje ćemo se samo kratko osvrnuti na neke specifičnosti 'deadbeat' vođenja povratnom vezom po varijablama stanja.
Pokažimo najprije zašto
sustav vođen 'deadbeat' regulatorom dođe u stacionarno stanje u najviše
onoliko diskretnih trenutaka koliko je red sustava. U ovoj ilustraciji
promatrati ćemo sustav koji nema ulazne pobude, već samo početne uvjete.
Njegovo ponašanje opisuje jednadžba (5.5.3) iz
poglavlja 5.5.1 uz to da stavimo r(kT)
= 0.Karakteristična jednadžba zatvorenog regulacijskog
sustava vođenog 'deadbeat' regulatorom glasi zn = 0. Prebacimo li
se u opis sustava varijablama stanja to znači da sve vlastite vrijednosti
matrice zatvorenog sustava 
trebaju biti jednake nuli. Prema Cayley-Hamiltonovom
teoremu (vidi Dodatak
A-1
Neki pojmovi matrične algebre)
iz toga slijedi da vrijedi i matrična jednadžba:
(5.5.38-2)
Množimo li sukcesivno
matricu samu sa sobom ništa se ne mijenja, pa vrijedi i sljedeći izraz
(5.5.38-3)
Prema jednadžbi (5.5.3) ponašanje zatvorenog regulacijskog sustava koji nema ulazne pobude, već samo početno stanje može se izračunati jednadžbom
(5.5.38-4)
a prema prethodnoj jednadžbi (5.5.38-3) očito je da je
(5.5.38-5)
'Deadbeat' regulator će u ovom slučaju, kada nemamo ulazne pobude, sve varijable stanja dovesti u konačno stanje jednako 0 za najviše onoliko diskretnih trenutaka koliki je red sustava, bez obzira na vrijednosti početnog stanje x(0).
Ako je sustav i dohvatljiv (vidi poglavlje 4.7.3 – Upravljivost i dohvatljivost) onda ga također možemo i iz bilo kojeg početnog stanja dovesti u bilo koje konačno stanje u istom broju diskretnih trenutaka vremena. 'Deadbeat' regulator će takav sustav dovesti u konačno stanje u nT diskretnih trenutaka, gdje je n red sustava. Jedina nezavisna varijabla u projektiranju 'deadbeat' regulatora je period uzorkovanja T. Teorijski mi sustav možemo dovesti u konačno stanje bez obzira koliki je T, ali još u prethodnoj diskusiji o 'deadbeat' vođenju (poglavlje 5.2.3.1) kazali smo da to zahtijeva vrlo velike vrijednosti i nagle promjene upravljačkog signala, što se najčešće ne može praktično realizirati. Rješenje kojim se može smanjiti upravljanje je povećanje perioda uzorkovanja T, ali to donosi druge probleme, na primjer loše potiskivanje poremećaja i veliku osjetljivost sustava vođenja na točnost modela vođenog dijela. Ovisnost 'deadbeat' vođenja o točnosti modela već smo diskutirali i ilustrirali primjerom u poglavlju 5.2.3.1. Što se tiče osjetljivosti na poremećaje, prisjetimo se da diskretni sustav vođenja reagira na poremećaje samo u diskretnim trenucima vremena (višekratnicima perioda uzorkovanja), a između njih miruje i na izlazu daje konstantnu vrijednost upravljačkog signala. Poremećaji su međutim prisutni stalno, pa veliki period uzorkovanja donosi loše potiskivanje poremećaja.
Zbog svega toga 'deadbeat' vođenje nije spasonosna, idealna metoda vođenja, pogodna za sve situacije, već baš suprotno, možemo je koristiti samo ukoliko je
a) model vođenog sustava pouzdan,
b) nema poremećaja koji djeluju na sustav i
c) ukoliko je moguće ostvariti velike vrijednosti i nagle promjene upravljačkog signala.
Proračun matrice povratne veze varijabli stanja za 'deadbeat' vođenje je isti kao kao prije s tim da se za karakteristični polinom uzme izraz (5.5.38-1) gdje je n red sustava.
Uzmimo primjer iz poglavlja 5.5.1.2. Jednadžbe varijabli stanja vođenog sustava su:
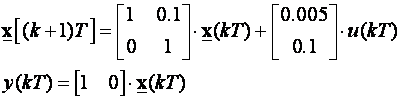
T=0.01, a željena karakteristična jednadžba vođenog sustava treba biti
Riješimo determinantu:
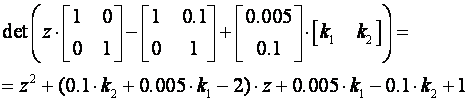
Izjednačavanjem koeficijenata uz iste potencije varijable z dobijemo sustav od dvije jednadžbe s dvije nepoznanice:
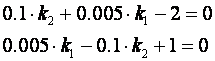
koje je lako riješiti, pa su koeficijenti povratne veze varijabli stanja:
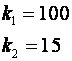
Slika 5.5.22-1 prikazuje odziv vođenog sustava na pobudnu funkciju jediničnog skoka.
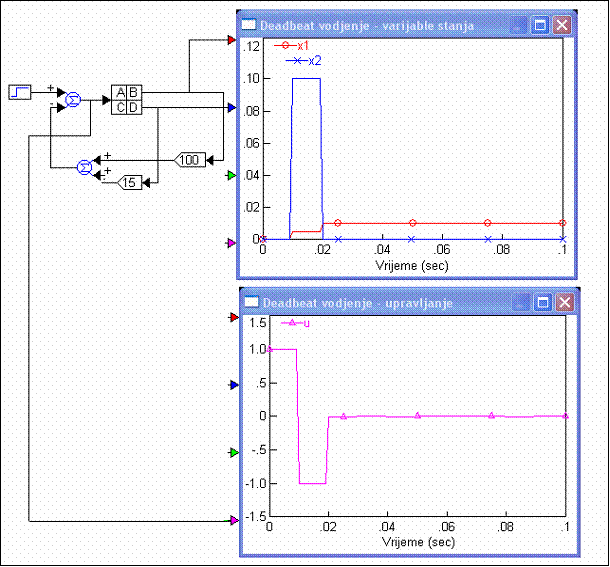
Slika 5.5.22-1. Odziv vođenog sustava (varijable_stanja_dedbeat.vsm)
Kako smo i pretpostavili sustav u dva diskretna trenutka vremena (2.T=2.0.01=0.02) dođe do konačne vrijednosti. Upravljački signal je alternirajući (s velike pozitivne ide na veliku negativnu vrijednost), a naravno pogreška ustaljenog stanja i ovdje postoji. Ustaljena vrijednost varijable stanja x1 je još manja nego u primjeru u poglavlju 5.5.1.2. Zato je možda bolje odzive uspoređivati za slučaj kada imamo samo početne vrijednosti, a konačne, željene vrijednosti varijabli stanja su 0. Slika 5.5.22-2 uspoređuje odzive istog sustava za dvije vrijednosti varijabli stanja koje smo izračunali u poglavlju 5.5.1.2 (k1=10, k2=3.5) i (k1=13, k2=3.35), te za vrijednosti 'deadbeat' vođenja povratnom vezom po varijablama stanja (k1=100, k2=15) za početni uvjet x1(0)=0.1.
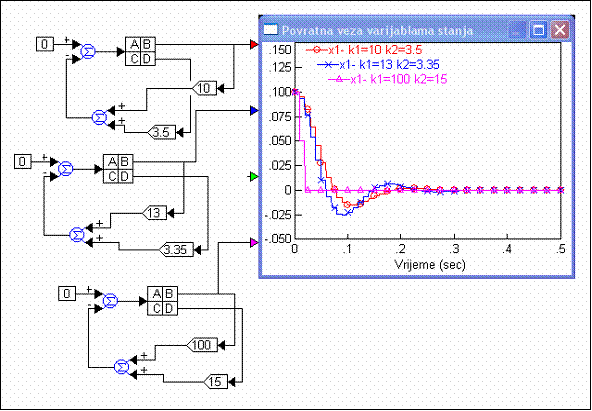
Slika 5.5.22-2. Usporedba odziva varijable stanja x1 za različite vrijednosti koeficijenata povratne veze varijabli stanja, ulazni signal jednak nuli i početni uvjet x1(0)=0.1 (varijable_stanja_deadbeat_2.vsm)
Posebno je zanimljivo pogledati upravljačke signale za ova tri slučaja. Prikazuje ih slika 5.5.22-3.
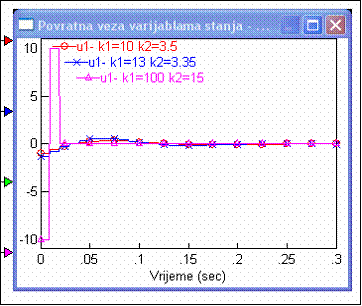
Slika 5.5.22-3. Usporedba upravljačkih signala za različite vrijednosti koeficijenata povratne veze varijabli stanja, ulazni signal jednak nuli i početni uvjet x1(0)=0.1 (varijable_stanja_deadbeat_2.vsm)
Kod standardnog vođenja povratnom vezom po varijablama stanja upravljačka varijabla nikada nema veću vrijednost od 0.5, dok kod 'deadbeat' regulatora ona alternira između -10 i +10.
U programima Matlab, Octave ili Scilab vrijednosti koeficijenata povratne veze varijabli stanja za 'deadbeat' vođenje računamo na isti način kao u poglavlju 5.5.1.2 s tim da vrijednosti korijena karakteristične jednadžbe stavljamo jednake 0.