5.5.2. Procjenitelji stanja (estimatori, opserveri ili osmotrivači)

Kod do svih sada opisanih postupaka vođenja temeljenih na povratnoj vezi varijabli stanja nužno je mjeriti vrijednosti varijabli stanja. Kako je u praksi česti slučaj da neke od varijabli stanja nisu pogodne za mjerenje, njih je na neki način potrebno odrediti, izračunati, estimirati na temelju vrijednosti varijabli stanja koje možemo mjeriti. Mjerljive varijable stanja su najčešće i izlazne varijable stanja pa se postavlja sljedeći zadatak:

Na temelju poznatih vrijednosti izlaznih veličina sustava y i upravljačkih veličina u odredi vrijednosti varijabli stanja x.

To je moguće učiniti procjenjujući stanje za trenutak kT na temelju vrijednosti ulaza u(kT) i izlaza y(kT) u tom istom trenutku vremena kT. Procijenjene varijable stanja označavamo a takve procjenitelje nazivamo procjenitelji bez predviđanja ili ne-prediktivni estimatori. Kod procjenitelja s predviđanjem ili prediktivnih estimatora procjenjujemo vrijednost varijabli stanja u trenutku kT na temelju vrijednosti ulaza u(k-1)T i izlaza y(k-1)T u trenutku (k-1)T. Procijenjene varijable stanja u ovom slučaju označavamo  .

Procjenitelji bez predviđanja su efikasni ukoliko je vrijeme proračuna procijenjenih varijabli puno kraće od perioda uzorkovanja. Ukoliko nije, ne ostaje ništa drugo nego koristiti procjenitelje s predviđanjem. Njihov je problem s druge strane taj što unose kašnjenje od jednog diskretnog trenutka vremena.

Druga podjela procjenitelja stanja je po broju varijabli koje procjenjujemo. Ukoliko se procjenjuju sve varijable stanja procjenitelje nazivamo potpuni procjenitelji stanja (eng. Full-Order Observer). Jedna od izvedbi potpunog procjenitelja stanja je  asimptotski potpuni procjenitelj stanja (eng. Asimptotic Full-Order Observer), o kojem detaljno govorimo u sljedećem poglavlju. Ukoliko se ne procjenjuju sve varijable stanja procjenitelje nazivamo reducirani procjenitelji stanja (eng. Reduce-Order Observer). Kod njih se određeni broj varijabli stanja mjeri a ostale se procjenjuju. U nastavku ćemo ukratko objasniti principe i ovog tipa procjenitelja stanja, ali prije toga objasnimo osnovnu ideju procjene stanja na primjeru potpunog asimptotskog procjenitelja stanja.

Slika 5.5.23 prikazuje stvarni sustav čije varijable stanja x(kT) ne možemo mjeriti i model sustava kojim procjenjujemo njihove vrijednosti  .

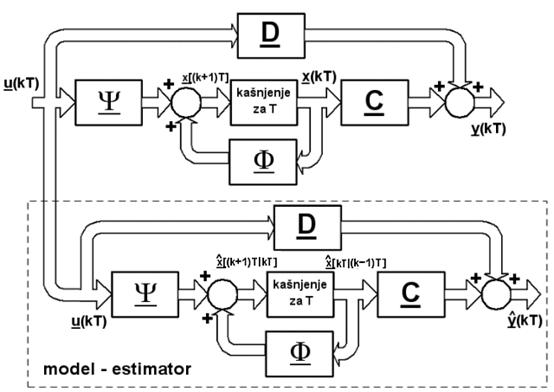
 Slika 5.5.23. Stvarni sustav i model sustava pomoću kojeg procjenjujemo varijable stanja koje nisu dostupne

Međutim:

- Naš model najčešće nije dovoljno precizan. Mi pretpostavljamo da su F, Y, C i D parametri stvarnog sustava, ali se stvarne vrijednosti obično razlikuju, koji put više, koji put manje, ovisno kako smo dobro i da li uopće možemo napraviti točnu identifikaciju parametara modela. Osim toga mi obično sustav pretpostavljamo linearnim, a uvijek postoje veće ili manje nelinearnosti.

- Najčešće ne znamo točne početne uvjete sustava.

- Sustav može biti pod utjecajem poremećaja w koje se ne mogu modelirati i uzeti u obzir kod formiranja modela procjenitelja stanja.

Konačni rezultat je taj da će procijenjene varijable stanja   odstupati od stvarnih vrijednosti x(kT). Zbog toga se uvodi povratna veza po procijenjenim vrijednostima izlaza    koji se uspoređuju sa stvarnim vrijednostima izlazima y(kT), za koje smo od početka pretpostavili da su dostupni i mjerljivi. Dobivena razlika se množi s matricom estimatora M i dodaje jednadžbi varijabli stanja. Ovakav tip procjenitelja stanja nazivamo Luenbergerov procjenitelj stanja (eng. Lunenberger Observer) . Situaciju prikazuje slika 5.5.24.
 

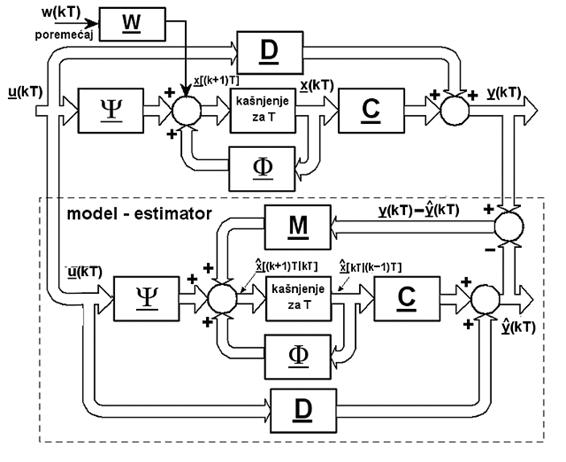
 Slika 5.5.24. Formiranje povratne veze estimatora kako bi se smanjila pogreška procjene

Ako sustav koji se vodi opišemo diskretnim jednadžbama varijabli stanja:

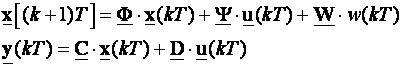          (5.5.39)

dinamička jednadžba procjenitelja stanja s predviđanjem (prediktivnog estimatora) će biti:

    (5.5.40)

Prema tome Luenbergerov procjenitelj stanja ima strukturu:

(procjenitelj stanja) = (kopija sustava koji se vodi) + (korekcijski član)

Koristi se prvenstveno za minimizaciju pogreške koja se javlja zbog nepoznavanja početnih uvjeta sustava koji se vodi.

Zbog preglednijeg iznošenja osnovnih postavki ovog tipa procjenitelja stanja, u nastavku ćemo se ograničiti na sustave kod kojih nema direktne veze upravljačkog ulaza i izlaza (matrica D je jednaka nul-matrici). Jednadžba (5.5.40) u tom slučaju glasi:

    (5.5.41)

Uvedimo pogrešku procjene:

       (5.5.42)

Nakon uvrštavanja dobijemo:

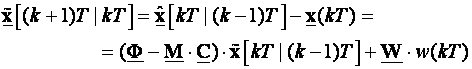     (5.5.43)

Uz pretpostavku točnog modela sustava i ne prisustva poremećaja pogreška procjene će težiti nuli ukoliko matricu M  odaberemo tako da sustav:

     (5.5.44)

bude asimptotski stabilan. Zato procjenitelj stanja i zovemo asimptotski procjenitelj stanja i o njemu detaljno govorimo u sljedećem poglavlju.

Već smo spomenuli da procjenitelj stanja s predviđanjem unosi kašnjenje od jednog diskretnog trenutka vremena.  zato što ovisi o mjerenjima u trenutku (k-1)T. Kod procjenitelja bez predviđanja ovog kašnjenja nema:

     (5.5.45)

Pogreška procjene koja odgovara jednadžbi (5.5.44) u ovom je slučaju:

     (5.5.46)

Jednadžbe (5.5.44) i (5.5.46) su vrlo slične. Odgovarajućim odabirom matrice M i ovdje je moguće vlastite vrijednosti matrice  postaviti bilo gdje, a mi naravno nastojimo kao i prije da sustav (5.5.46) bude asimptotski stabilan.