5.5.2.2. Reducirani procjenitelj stanja
U dosadašnjim smo razmatranjima promatrali procjenitelje stanja pomoću kojih procjenjujemo sva stanja sustava koji se vodi. Ukoliko neka od stanja možemo mjeriti, njih nije potrebno procjenjivati. Pri tome treba imati na umu da je ponekad, ukoliko su mjerene veličine 'onečišćene' smetnjama, pogodnije koristiti asimptotski procjenitelj stanja koji procjenjuje vrijednosti varijabli stanja bez smetnji. Za sada ćemo pretpostaviti da su izmjerene vrijednosti varijabli stanja pouzdane i da će reducirani procjenitelj stanja davati točnije rezultate s obzirom da se rekonstruiraju samo neke od varijable stanja. Osim toga reducirani procjenitelj stanja je nižeg reda pa je i proračun brži.
Projektiranje reduciranog procjenitelja stanja svodi se na particiju vektora varijabli stanja na direktno mjerljive varijable stanja xa i nemjerljive varijable stanja xb:
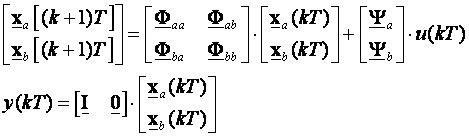 (5.5.62)
(5.5.62)
Promatramo odvojeno dinamičko ponašanje nemjerljivih i mjerljivih varijabli stanja:
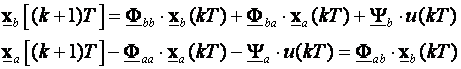 (5.5.63)
(5.5.63)
U prvoj jednadžbi,
zadnja dva pribrojnika na desnoj strani
![]() predstavljaju ‘poznate ulaze’
za nepoznate varijable stanja koje trebamo estimirati.
Druga je jednadžba napisana tako da cijeli izraz na lijevoj strani
predstavljaju ‘poznate ulaze’
za nepoznate varijable stanja koje trebamo estimirati.
Druga je jednadžba napisana tako da cijeli izraz na lijevoj strani
![]() predstavlja ‘poznate izlaze’.
predstavlja ‘poznate izlaze’.
Jednadžba ne-reduciranog procjenitelja stanja je:
![]() (5.5.64)
(5.5.64)
Uvrstimo li jednadžbe (5.5.62) razdvojenog modela sustava dobijemo jednadžbu reduciranog procjenitelja stanja. Pri tome s 'poznatim ulazima' u jednadžbi (5.5.63) zamjenjujemo u(kT), a s 'poznatim izlazima' y(kT):
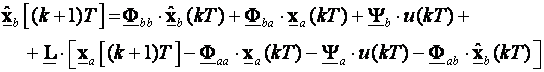 (5.5.65)
(5.5.65)
gdje je L matrica reduciranog procjenitelja stanja. Ona treba biti dimenzija [(n-m)xm] gdje je n red sustava, a m broj mjerljivih varijabli stanja. Pogreška procjene je:
![]() (5.5.66)
(5.5.66)
što znači da matricu procjenitelja stanja L možemo računati na isti način kao kod asimptotskog procjenitelja stanja, s tim da umjesto matrice F imamo Fbb, a umjesto matrice C matricu Fab. Matlab program za proračun matrice procjenitelja stanja L je:
Fi_bb = ...
Fi_ab = ...
polinom=[z1;z2;...]
L=place(Fi_bb',Fi_ab',polinom)'
Scilab program glasi:
Fi_bb = ...
Fi_ab = ...
polinom=[z1,z2,...]
L=place(Fi_bb',Fi_ab',polinom)
L=L'
a Octave:
Fi_bb = ...
Fi_ab = ...
c= ...
t=...
sys=ss2sys(Fi_bb',Fi_ab',c,d,t)
z1= ...
korijeni=[z1,z2,...]
L=place(sys,korijeni)'
Sredimo li jednadžbu (5.5.65) dobiti ćemo:
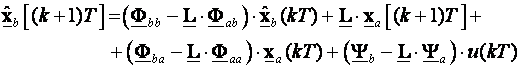 (5.5.67)
(5.5.67)
Prema jednadžbi (5.5.67) za proračun nemjerljivih varijabli stanja u trenutku (k+1)T treba nam vrijednost mjerljivih varijabli stanja xa u trenucima (k+1)T i kT. Nama za vođenje povratnom vezom varijabli stanja treba vrijednost nemjerljivih varijabli stanja xb u trenutku kT, pa jednadžbu (5.5.67) snižavamo za jedan diskretni trenutak vremena:
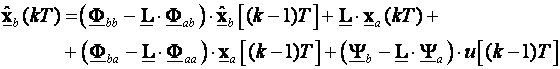 (5.5.68)
(5.5.68)
Upravljačka veličina sustava vođenog povratnom vezom varijabli stanja je
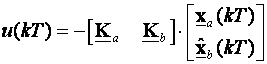 (5.5.69)
(5.5.69)
pa vođenje povratnom vezom varijabli stanja uz reducirani procjenitelj stanja možemo prikazati slikom 5.5.33.
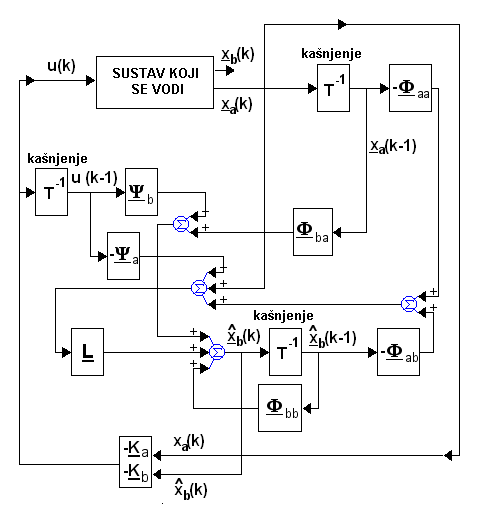
Slika 5.5.33. Povratna veza varijablama stanja estimiranim reduciranim procjeniteljem stanja
Kod asimtotskog procjenitelja stanja u trenutku kT estimirali smo varijable stanja na temelju poznavanja izlaza i ulaza u trenutku kT, dok nam kod reduciranog procjenitelja stanja trebaju izlazi (koji ovdje odgovaraju mjerljivim varijablama stanja) i ulazi i u trenutku kT i u trenutku (k-1)T. Reducirani procjenitelj stanja mora pamtiti i prošle vrijednosti.
Napišimo pregledno sve jednadžbe vođenja povratnom vezom varijabli stanja procijenjenih reduciranim procjeniteljem stanja:
i) Jednadžbe stanja vođenog sustava su
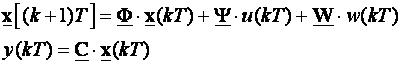
Matrica poremećaja W je nepoznata, pa je izostavljamo iz daljnjeg proračuna. Razdvojimo mjerljive xa i nemjerljive varijable stanja xb te napravimo particiju matrica sustava:
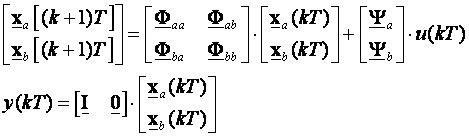
ii) Jednadžba varijabli stanja procjenitelja stanja je
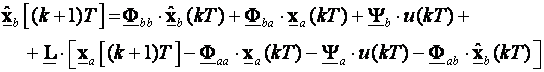
iii) Matricu procjenitelja stanja L računamo iz jednadžbe
![]()
gdje je PO(z) željeni karakteristični polinom procjenitelja stanja:
![]()
matrica L je dimenzija [(n-m) x m] gdje je n red sustava, a m broj mjerljivih varijabli stanja
iv) Upravljačka veličina vođenog sustava je
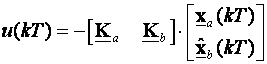
v) Matricu povratne veze varijabli stanja
![]()
računamo iz polazne jednadžbe
![]()
gdje je PS(z) željeni karakteristični polinom vođenog sustava:
![]()
Dodavanjem zakona upravljanja jednadžbi procjenitelja stanja dobijemo:
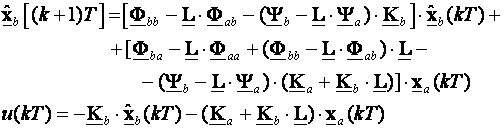 (5.5.70)
(5.5.70)
Ovo je jednadžba varijabli stanja ekvivalentnog povratnog regulatora čiji je izlaz upravljanje u(kT) a ulaz mjerljive varijable stanja xa. Radi se o ekvivalentnom povratnom regulatoru s više ulaza i jednim izlazom (MISO regulator) pa je impulsna prijenosna funkcija regulatora matrična funkcija koju računamo jednadžbom:
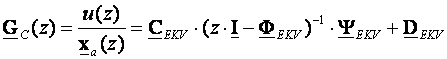 (5.5.71)
(5.5.71)
gdje su:
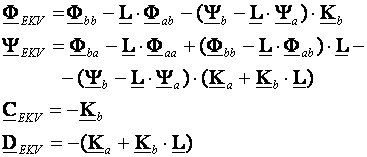 (5.5.72)
(5.5.72)
Vođenje sustava povratnom vezom varijabli stanja i reduciranim procjeniteljem stanja ilustrirati ćemo na primjeru.
Primjer:
Analizirati ćemo sustav trećeg reda iz prethodnog primjera čije su diskretne jednadžbe varijabli stanja:
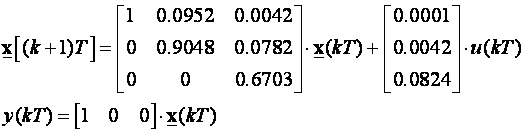
Prisjetimo se za T=0.1 ovaj diskretni sustav odgovara kontinuiranom sustavu čiji je blok prikaz vođenog sustava s označenim varijablama stanja prikazan na slici 5.5.29.
Najprije ćemo pretpostaviti da su prve dvije varijable stanja mjerljive, a treća nemjerljiva, pa će vektor mjerljivih varijabli stanja biti:
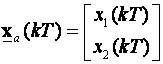
a vektor ne-mjerljivih samo:
![]()
Particija matrica F i Y daje:
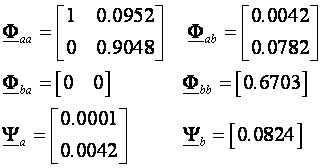
Procjenitelj stanja je prvog reda (estimiramo samo varijablu stanja x3). Proračunati ćemo ga kao i u prethodnom primjeru na temelju Besselovih polinoma uz uvjet da vrijeme smirivanja na 1% vrijednosti T1% bude 0.5 sekundi. Procjenitelj stanja je prvog reda pa iz tablice na slici 5.5.4 uzimamo pol normaliziranog Besselovog polinoma prvog reda B1(s): p1 = -4.62. Ova vrijednost vrijedi za vrijeme smirivanja 1 sekundu. Za 0.5 sekundi vrijednost trebamo dijeliti sa 0.5: p1 = -4.62/0.5 = -9.24. Ostaje nam još prebaciti se u z područje za T=0.1: p01 =e-9.24*0.1 = 0.3969. Željeni karakteristični polinom procjenitelja stanja je prema tome: Po=z-0.3969. Matrica procjenitelja stanja je reda [(n-m)xm], a kako je u našem slučaju n=3, a m=2 matrica procjenitelja stanja je reda [1 x 2]. Računamo je iz izraza:
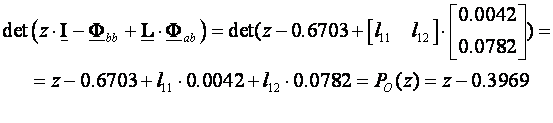
Jedan od koeficijenata možemo u principu odrediti proizvoljno, a drugi izračunamo na primjer:
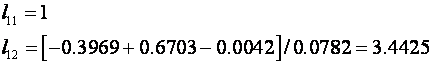
ali u simulaciji ćemo koristiti vrijednosti koje daje Matlab funkcijom place (Matlab program možete pronaći na našem poslužitelju pod nazivom asimptotski_3.m):
![]()
(Napomena: S obzirom da je matrica L reda [1 x 2] funkciju place programa Octave ne možemo koristiti. Ona je ograničena samo na sustave gdje je L reda [n x 1] .)
Povratni smo regulator za vrijeme smirivanja od 2 sekunde već izračunali u prethodnom primjeru. Rezultat je:
![]()
Slika 5.5.34 prikazuje vremenske promjene varijabli stanja sustava vođenog povratnom vezom varijabli stanja za početne uvjete
![]()
u slučaju bez procjenitelja stanja i uz procjenu treće varijable stanja reduciranim procjeniteljem stanja. Procjenitelja stanja u VisSimu smo modelirali prema slici 5.5.33 (pogledaj u Vissimu varijable_stanja_estimatori_3.vsm).
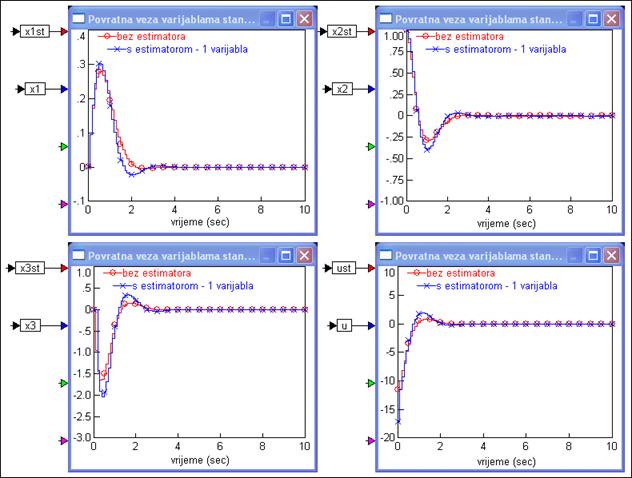
Slika 5.5.34. Usporedba odziva varijabli stanja sustava vođenog povratnom vezom varijablama stanja bez procjenitelja stanja (ulaz u regulator su stvarne vrijednosti varijabli stanja) i s reduciranim procjeniteljem stanja koji procjenjuje samo treću varijablu stanja a) varijabla stanja x1(kT), b) varijabla stanja x2(kT), c) varijabla stanja x3(kT), d) upravljanje u(kT) (varijable_stanja_estimatori_3.vsm)
==========================================
Pretpostavimo sada da je mjerljiva samo varijabla stanja x1. Vektor mjerljivih varijabli stanja je sada:
![]()
a vektor ne-mjerljivih samo:
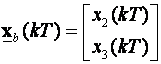
Particija matrica F i Y daje:

Procjenitelj stanja je sada drugog reda. Ostaviti ćemo isto vrijeme smirivanja na 1% vrijednosti T1% od 0.5 sekundi. Procjenitelj stanja Iz tablice na slici 5.5.4 uzimamo pol normaliziranog Besselovog polinoma drugog reda B2(s): p1 = -4.053+j2.340 i p2 = -4.053-j2.340. Za 0.5 sekundi vrijednosti trebamo podijeliti sa 0.5: p1 = -4.053/0.5 +j2.340/0.5 = -8.106+j4.68 i p2 = -4.053/0.5 -j2.340/0.5 = -8.106-j4.68. U z području za T=0.1 imamo p01 =0.3968+j0.2 i p02 =0.3968-j0.2. Željeni karakteristični polinom procjenitelja stanja je prema tome: Po=z2-0.7936 z+0.19745 . Matrica procjenitelja stanja je reda [2 x 1] i računa se iz izraza:
![]()
Rezultat je
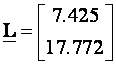
Napomena: Vrijednosti smo izračunali programom Octave. Program je bio:
Slika 5.5.35 prikazuje vremenske promjene varijabli stanja sustava vođenog povratnom vezom varijabli stanja za početne uvjete
![]()
u slučaju bez procjenitelja stanja i uz procjenu treće varijable stanja reduciranim procjeniteljem stanja. Procjenitelja stanja smo u VisSimu također modelirali prema slici 5.5.33.
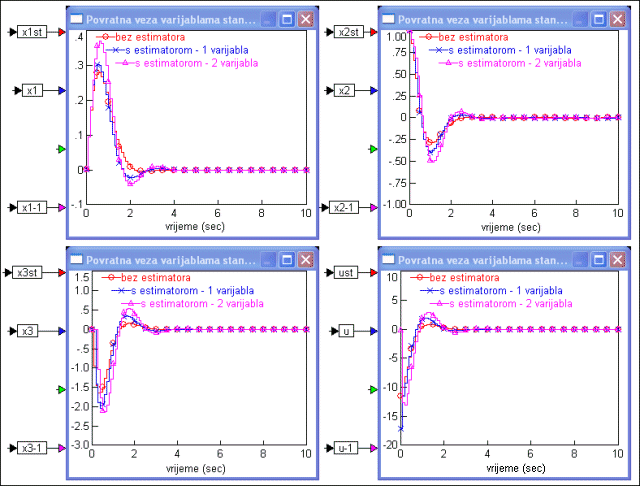
Slika 5.5.35. Usporedba odziva varijabli stanja sustava vođenog povratnom vezom po varijablama stanja bez procjenitelja stanja (ulaz u regulator su stvarne vrijednosti varijabli stanja) i s reduciranim procjeniteljima stanja koji procjenjuju varijablu stanja x3(kT) odnosno varijable stanja x2(kT) i x3(kT): a) varijabla stanja x1(kT), b) varijabla stanja x2(kT), c) varijabla stanja x3(kT), d) upravljanje u(kT) (varijable_stanja_estimatori_4.vsm)
Napomenimo da se i u slučaju VisSim simulacija koje prikazuje slika 5.5.34 i slika 5.5.35 u povratnoj grani javi algebarska petlja koju VisSim sam razriješi uvođenjem kašnjenja, ali relativni odnosi ostaju sačuvani.
Matlab program za proračun reduciranog procjenitelja stanja i simulaciju zatvorenog sustava vođenje prema jednadžbi (5.5.72) nalazi se na našem poslužitelju pod nazivom asimptotski_4.m). Slika 5.5.36 prikazuju vremenske promjene varijabli stanja sustava, a slika 5.5.37 usporedbu stvarnih i procijenjenih varijabli stanja.
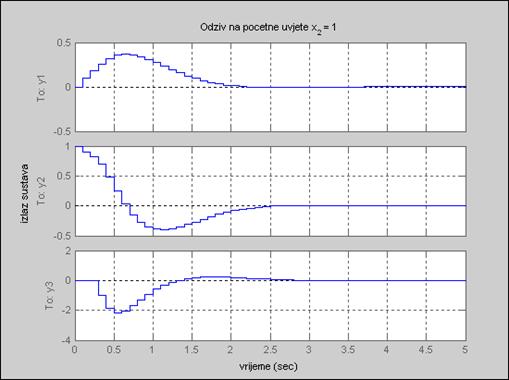
Slika 5.5.36. Varijable stanja sustava za reducirani procjenitelj stanja kojim procjenjujemo dvije varijable stanja za početne uvjete x(0)= [0 1 0]T (asimptotski_4.m)
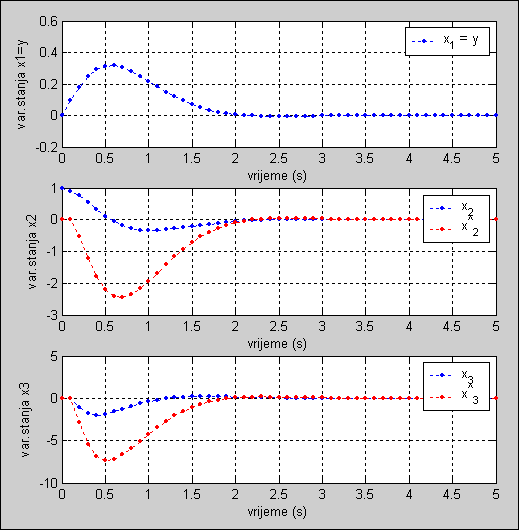
Slika 5.5.37. Usporedba stvarnih (simuliranih) i procijenjenih varijabli stanja. Razlika postoji zato što su početni uvjeti procjenitelja stanja jednaki nuli, a početni uvjeti sustava su bili x(0)= [0 1 0]T (asimptotski_4.m)
I kod reduciranih procjenitelja stanja promatrali smo samo sustave bez referentnog ulaza. Kako se matrica povratne veze varijabli stanja određuje potpuno neovisno od matrice procjenitelja stanja, prijelaz na slijedno vođenje je i ovdje direktan. Može se primijeniti bilo koji postupak iz poglavlja 5.5.1.4 Slijedno vođenje povratnom vezom varijabli stanja s tim da se umjesto izmjerenih varijabli stanja koriste procijenjene varijable stanja.