5.5.2.1. Asimptotski potpuni procjenitelji stanja
Izučavamo
procjenitelja stanja s predviđanjem (prediktivnog asimptotskog estimatora).
Zbog jednostavnosti pisanja izostaviti ćemo duplo označavanje diskretnih
vremenskih trenutaka, pa ćemo umjesto
pisati samo
, a umjesto
samo 
s
jednim upravljačkim ulazom u(kT) i jednim izlazom y(kT). Polazna je jednadžba
u tom slučaju:
(5.5.47)
Matrica procjenitelja M je u biti matrica pojačanja pogreške procjene stanja. Jednadžbu (5.5.47) dalje možemo napisati u obliku:
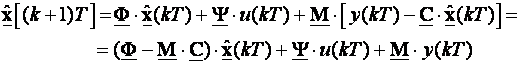(5.5.48)
pa je
pogreška procjene 
:
(5.5.49)
Ona je ekvivalentna izrazu (5.5.43).
Uz pretpostavku točnog modela sustava i ne prisustva poremećaja pogreška procjene će asimptotski težiti nuli ukoliko odaberemo odgovarajuću matricu M. U stvarnosti uvijek će međutim postojati određena pogreška procjene. Model nikada nije savršen i poremećaji su više, manje uvijek prisutni. Ovu pogrešku možemo držati dovoljno malom ukoliko vlastite vrijednosti matrice (F - M C) budu dovoljno prigušene i brze u odnosu na dinamiku zatvorenog, vođenog sustava.
Matricu M računamo na isti način kao što smo računali matricu povratne veze varijabli stanja K. Željene dinamičke karakteristike procjenitelja stanja definiramo željenim polinomom. Izračunamo njegove korijene te upravo njih izabiremo za vlastite vrijednosti matrice (F - M C):
(5.5.50)
Temeljna jednadžba proračuna je:
(5.5.51)
pa se može koristiti ista funkcije programa Matlab ili Octave (place() – vidi poglavlje 5.5.1.2) uz male izmjene o kojima ćemo detaljnije govoriti kasnije. Naravno uz sve to vođeni sustav treba biti osmotriv (opservabilan).
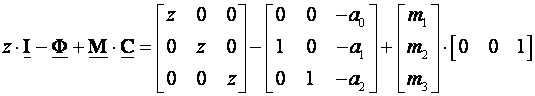(5.5.52)
Proračunamo li determinantu dobiti ćemo:
(5.5.53)
Ako je željeni polinom estimatora
(5.5.54)
vrijednosti koeficijenata matrice estimatora su
(5.5.55)
Povežemo li asimptotski procjenitelj stanja s povratnom vezom varijabli stanja dobiti ćemo shemu prikazanu na slici 5.5.25.
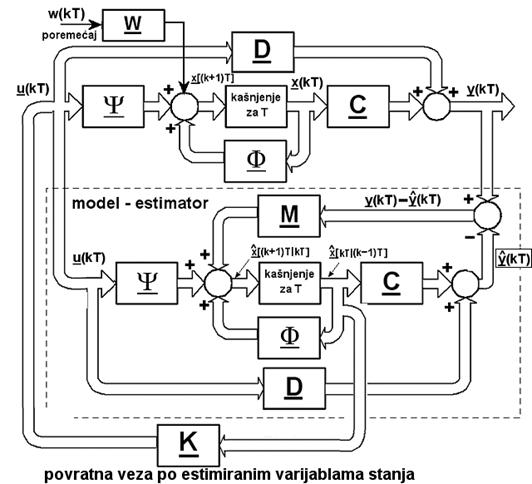
Slika 5.5.25. Povratna veza varijablama stanja procijenjenim asimptotskim estimatorom
Matricu povratne veze varijabli stanja računamo nezavisno koristeći standardne jednadžbe za proračun povratne veze varijabli stanja iz poglavlja 5.5.1.2.
i) Jednadžbe stanja vođenog sustava:
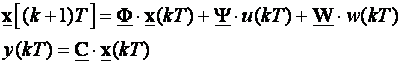
(matrica poremećaja W je nepoznata).
ii) Jednadžba asimptotskog potpunog procjenitelja stanja:
iii) Matricu procjenitelja stanja M računamo iz jednadžbe
gdje je PO(z) željeni karakteristični polinom procjenitelja stanja:
iv) Upravljačka veličina vođenog sustava je
v) Matricu povratne veze varijabli stanja K računamo iz jednadžbe
gdje je PS(z) željeni karakteristični polinom vođenog sustava:
vi) Dodavanjem upravljačkog signala jednadžbi procjenitelja stanja i sređivanjem dobijemo
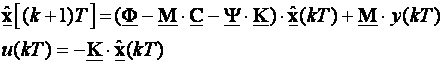
Ova posljednja jednadžba je jednadžba koju možemo koristiti za proračun ekvivalentnog povratnog regulatora koji uključuje i asimptotski procjenitelj stanja i povratnu vezu po varijablama stanja. O njegovom ćemo proračunu u nastavku detaljnije pisati, ali najprije pogledajmo na jednom primjeru kako računamo matricu procjenitelja stanja i matricu povratne veze varijabli stanja.
Procjenitelja stanja i povratnu vezu varijablama stanja računali smo potpuno nezavisno. To je princip odvojivosti ili princip separacije (eng. Separation Principle) koji vrijedi kod linearnih sustava. Možemo ga opisati i na sljedeći način: Stabilnost sustava ovisi o članovima (F - Y K) i (F - M C). Povratnu vezu varijabli stanja K možemo izračunati tako da (F - Y K) bude stabilan samo onda ukoliko je sustav (F , Y ) upravljiv, a M možemo izračunati tako da (F - M C) bude stabilan samo onda ukoliko je sustav (F , C ) osmotriv.
Pogledajmo sada jedan primjer proračuna asimptotskog potpunog procjenitelja stanja.
Uzeti ćemo isti primjer dvostrukog integratora kao i u poglavlju 5.5.1.2:
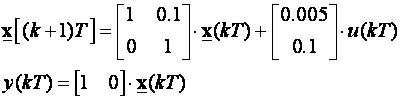
Period uzorkovanja je T=0.01. Željeni karakteristični polinom vođenog sustava je
pa je povratna veza varijabli stanja
Pretpostavimo da je željeni karakteristični polinom estimatora
Matricu estimatora računamo iz jednadžbe:
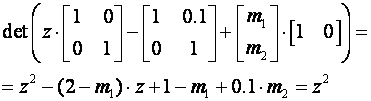
Dalje slijedi:
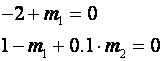
i na kraju dobijemo
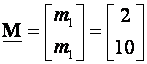
Slika 5.5.26 prikazuje odziv zatvorenog regulacijskog sustava vođenog povratnom vezom varijabli stanja i asimptotskim estimatorom za nultu pobudu i početne uvjete x1 = 0.1 u usporedbi s vođenjem povratnom vezom varijabli stanja bez estimatora.
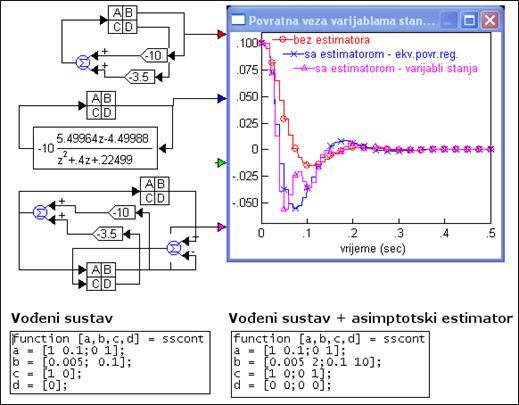
Slika 5.5.26. Odziv sustava vođenog povratnom vezom varijabli stanja i asimptotskim procjeniteljem stanja i bez procjenitelja stanja (ulaz u regulator su stvarne vrijednosti varijabli stanja) za nultu pobudu i početni uvjet x1 = 0.1 i T=0.01 (varijable_stanja_estimatori_1.vsm)
Odziv sustava s procjenom stanja je lošiji od odziva sustava bez procjene stanja, što je bilo i za očekivati.
Na slici su uspoređene i dvije verzije sustava s procjeniteljem stanja. Prva se temeljila na ekvivalentnom povratnom regulatoru o kojem smo već govorili i kojeg ćemo detaljnije analizirati u nastavku. Kod druge je procjenitelj također bio modeliran jednadžbama varijabli stanja. Polazna jednadžba je bila (5.5.41) kod koje je vektor procjene M pridružen vektoru upravljačkog signala Y:
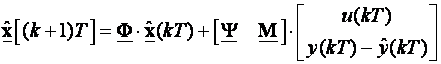
Vrijednosti te nove matrice vanjske pobude prikazane su na slici 5.5.25 i označene slovom b. U odzivima sustava kod kojih procjenitelja stanja realiziramo na različite načine pojavljuje se određena razlika. Razlog je taj što se u slučaju modeliranja procjenitelja stanja varijablama stanja kod simulacije u VisSimu javi algebarska petlja (pojavi se upozorenje Algebraic loop), zato što se izlaz bloka koji se računa dovodi na ulaz istog bloka. Situaciju pojašnjava slika 5.5.27).
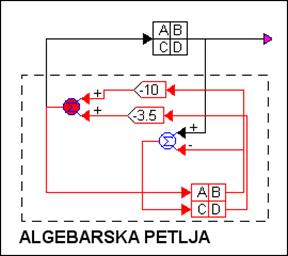
Slika 5.5.27. Pojava algebarske petlje u VisSimu kod simulacije procjenitelja stanja varijablama stanja (varijable_stanja_estimatori_1.vsm)
VisSim algebarsku petlju razrješava tako da sam uvodi kašnjenje ulaznih signala. Ovo kašnjenje uzrokuje pojavu odstupanja jednog i drugog načina simulacije, a simulacija s ekvivalentnim povratnim regulatorom je točnija.
Kod simulacije vođenog sustava u Matlabu također se koristi postupak temeljen na formiranju ekvivalentnog povratnog regulatora za koji Matlab ima i posebnu funkciju reg(Gp,K,L,sensors,known,controls) o čemu ćemo više govoriti u sljedećem poglavlju. Ovdje ćemo samo spomenuti da Matlab datoteku asimptotski_1.m sa simulacijom sustava sa slike 5.5.26 možete naći na našem poslužitelju. Odziv diskretnog sustava s estimatorom simuliranom u Matlabu, te usporedba stvarnih i procijenjenih varijabli stanja prikazana je na slici 5.5.28.
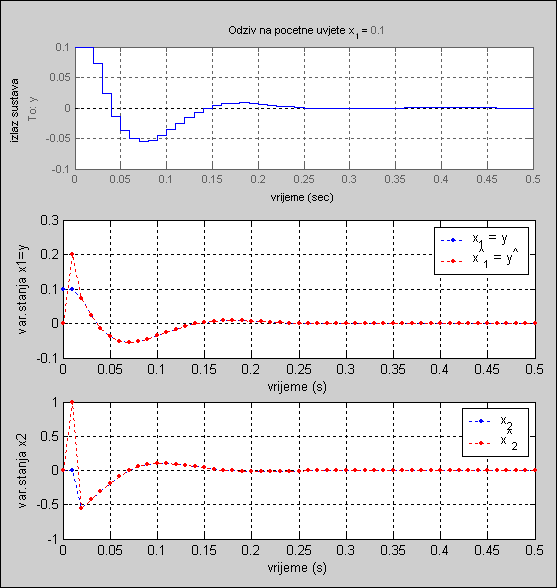
Slika 5.5.28. Odziv sustava sa slike 5.5.26, simuliranog u Matlabu, kod kojeg se varijable stanja estimiraju (izlaz sustava te usporedba stvarnih i procijenjenih varijabli stanja) (Matlab datoteka asimptotski_1.m)
Razlika između stvarnih i procijenjenih varijabli stanja javlja se zbog toga što su početni uvjeti procjenitelja stanja postavljeni na nulu. Ukoliko bi i estimator stanja imao iste početne uvjete kao i vođeni sustav razlika se ne bi pojavila . Naravno sve se to odnosi na simulacije. U stvarnim uvjetima razlike će uvijek postojati, zato što uvijek postoji odstupanje modela i početni se uvjeti često ne mogu točno procijeniti. Zato i postoji povratna veza estimatora i matrica M zbog koje razlike nakon nekog vremena nestaju što i pokazuje slika 5.5.28.
Vratimo se sada na numerički problem proračuna matrice procjenitelja stanja M programima Matlab i Octave. Funkcija place() je prvenstveno napisana za proračun matrice koeficijenata povratne veze varijabli stanja
Vektor K se u programu Matlab računa naredbama:
Fi = ...
Psi = ...
polinom=[z1;z2;...]
K=place(Fi,Psi,polinom)
u programu Scilab naredbama:
Fi = ...
Psi = ...
polinom=[z1,z2,...]
K=ppol(Fi,Psi,polinom)
a u programu Octave naredbama:
Fi = ...
Psi = ...
c= ...
d= ...
t= ...
sys=ss2sys(Fi,Psi,c,d,t)
z1= ...
korijeni=[z1,z2;...]
K=place(sys,korijeni)
Da bismo istu funkciju mogli koristiti i kod proračuna matrice procjenitelja stanja M prema jednadžbi
trebamo transponirati pojedine matrice i vektore. Oznaka za transponiranu matricu je literal ', pa u programu Matlab imamo:
Fi = ...
Psi = ...
polinom=[z1;z2;...]
M=place(Fi',c',polinom)'
u programu Scilab:
Fi = ...
Psi = ...
polinom=[z1,z2;...]
M=place(Fi',c',polinom)
M=M'
a u programu Octave:
Fi = ...
Psi = ...
c= ...
d= ...
t=...
sys=ss2sys(Fi',c',c,d,t)
z1= ...
korijeni=[z1,z2,...]
M=place(sys,korijeni)'
U on-line verziji programa Octave lako je provjeriti podatke na prethodnom primjeru: