3.5.5. Određivanje matrica varijabli stanja iz impulsne prijenosne funkcije – jednoveličinski sustav
Zanima nas inverzni zadatak. Zadana je impulsna prijenosna funkcija
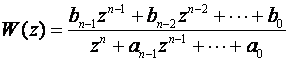(3.5.31)
Trebamo je prebaciti u jednadžbe varijabli stanja. To je moguće učiniti na nekoliko načina. Jedan od njih je da jednadžbe varijabli stanja definiramo na sljedeći način
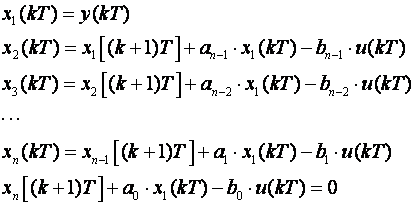(3.5.32)
Napišemo li jednadžbu (3.5.32) u obliku matričnih jednadžbi dobijemo
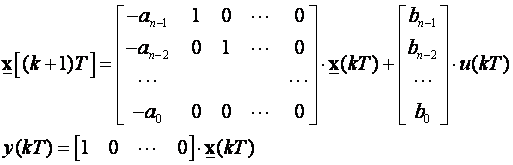(3.5.33)
Nema garancije za upravljivost i osmotrivost ovako dobivenog sustava (za svojstvo upravljivosti i osmotrivosti pogledajte poglavlje 4).
Ako znamo da je sustav upravljiv možemo primijeniti sljedeću transformacijsku jednadžbu:
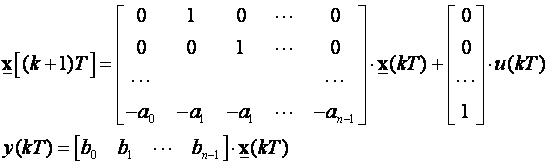(3.5.34)
Ako je sustav osmotriv transformacijske jednadžbe su:
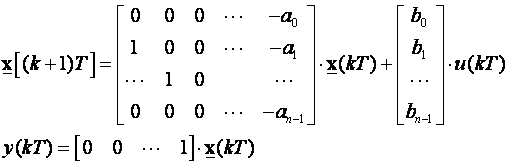(3.5.35)
Primjer:
Prebacimo impulsnu prijenosnu funkciju koju smo dobili u prethodnom poglavlju natrag u jednadžbe varijabli stanja:
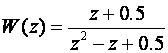
Vrijedi a0=0.5, a1=-1, b0=0.5 i b1=1, pa je:
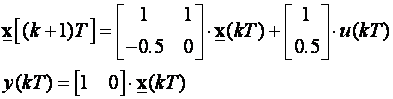
što su upravo one vrijednosti iz kojih smo izveli impulsnu prijenosnu funkciju.
Upravljiva realizacija daje
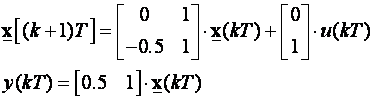
a osmotriva
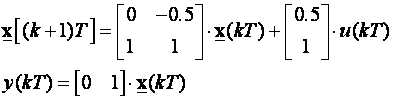
Naravno da sve tri realizacije daju isti odziv kao što prikazuje slika 3.5.6
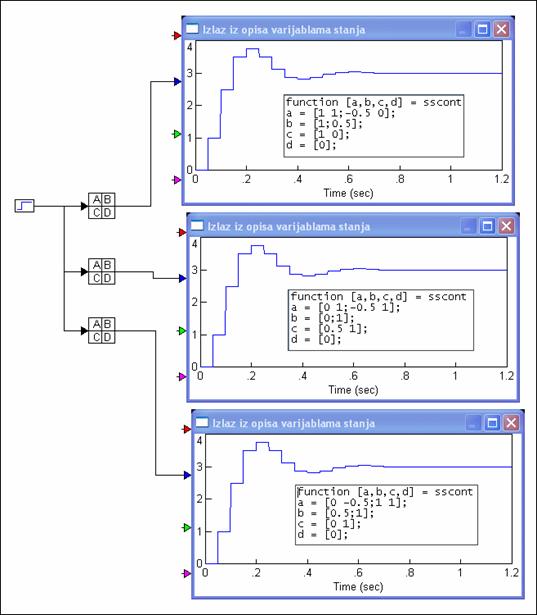
Slika 3.5.6. Odzivi sustava opisanog varijablama stanja izvedenog iz matrične impulsne prijenosne funkcije za T=0.05 (varijable_stanja_simulacija.vsm)