Digitalno vođenje on-line (FESB, Split)

3.5.6. Određivanje matrica varijabli stanja iz matrične impulsne prijenosne funkcije – viševeličinski sustav

Cilj: Naučiti kako iz matrične impulsne prijenosne funkcije odrediti jednadžbe varijabli stanja za viševeličinski sustav, uz ograničenje da sustav nema višestrukih polova.

Kod viševeličinskih sustava situacija je dosta složenija. Ovdje ćemo navesti samo postupak koji se odnosi na matričnu impulsnu prijenosnu funkciju koja nema višestrukih polova, što je u praksi česta pojava. Za općeniti slučaj čitaoca upućujemo na literaturu (npr. J.A. Borrie, Modern Control Systems, A Manual of Design Methods, Prentice Hall, 1986).

Dobivena realizacija je i osmotriva i upravljiva. Postupak je relativno jednostavan i sastoji se od 5 koraka:

1. Izračunati W(∞)

2. Pronaći W_r(z) = W(z)-W(∞)

3. Izraziti W_r(z) u obliku:

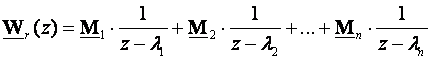(3.5.36)

gdje su λ₁ do λ_n svi polovi od W_r(z).

4. Rastaviti (dekompozirati) matrice M_i u oblik

(3.5.37)

gdje je L_i vektor, a N_i jednoredna matrica.

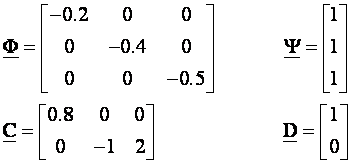
5. Matrice varijabli stanja su

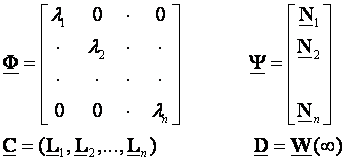(3.5.38)

Primjer:

Zadana je matrična impulsna prijenosna funkcija

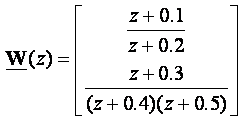
Polovi se nalaze u točkama

pa dalje slijedi

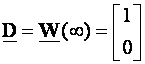
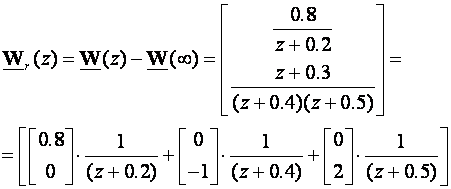
gdje su vektori residuumi prijenosnih funkcija. Dalje radimo njihovu dekompoziciju na vektore L i jednoredne matrice N_i koje su u ovom slučaju veličine 1x1:

pa je

Slika 3.5.7 prikazuje odzive sustava za opis varijablama stanja i opis impulsnom prijenosnom funkcijom. Odzivi su identični.

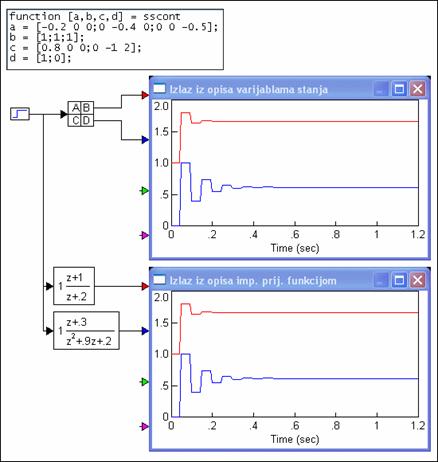
Slika 3.5.7. Odzivi sustava opisanog varijablama stanja izvedenog iz matrične impulsne prijenosne funkcije za T=0.05
(varijable_stanja_prelaz _iz_impulsne.vsm)

Pogledajmo na kraju kako odrediti matrice varijabli stanja zatvorenog regulacijskog sustava sastavljenog od diskretnog regulatora i diskretiziranog kontinuiranog sustava, oba opisana svojim jednadžbama varijabli stanja. O tome govori sljedeće poglavlje.