3.5.6. Određivanje matrica varijabli stanja zatvorenog regulacijskog sustava
Pogledajmo na kraju kako odrediti matrice varijabli stanja zatvorenog regulacijskog sustava sastavljenog od diskretnog regulatora i diskretiziranog kontinuiranog sustava, oba opisana svojim jednadžbama varijabli stanja. Sustav prikazuje slika 3.5.8.
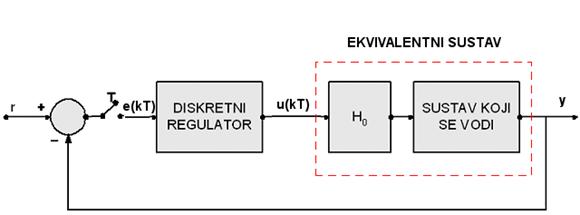
Slika 3.5.8. Diskretni regulacijski sustav (sve su veličine u općem slučaju vektorske)
Prvi je korak proračunati diskretne jednadžbe varijabli stanja kontinuiranog sustava. Varijable stanja digitalnog regulatora dodati ćemo varijablama stanja ekvivalentnog sustava. Pretpostavimo da ekvivalentni sustav ima n varijabli stanja, digitalni regulator m varijabli stanja, tako da zajedno imaju n+m varijabli stanja. Ulazi (pobude novog proširenog sustava biti će i upravljanje u(kT) i pogreška e(kT) pa nova jednadžba varijabli stanja složenog sustava glasi:
(3.5.38)
Za diskretni regulator možemo pisati
(3.5.39)
a za ekvivalentni kontinuirani sustav
(3.5.40)
Dalje možemo pisati
(3.5.41)
a iz (3.5.39) i (3.5.41) slijedi
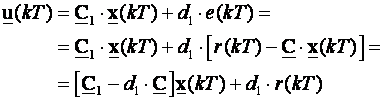(3.5.39)
Uvrstimo li sve to u (3.5.38) dobijemo
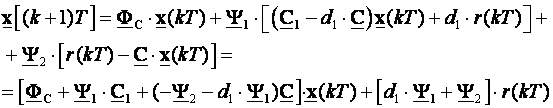
(3.5.38)
Jednadžba je duga i teško pregledna pa je najbolje ilustrirati je primjerom.
Primjer:
Sustav je prikazan na slici 3.5.9. Zadatak je zatvoreni regulacijski sustav opisati jednadžbama varijabli stanja za T = 0.1.
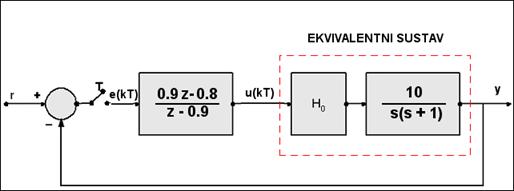
Slika 3.5.9. Diskretni regulacijski sustav
Za T = 0.1 ekvivalentni sustav možemo opisati jednadžbama varijabli stanja:
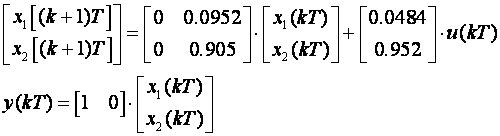
Digitalni regulator je prvog reda, pa ga opisujemo samo jednom varijablom stanja. Njegov je ulaz e(kT), a izlaz u(kT):
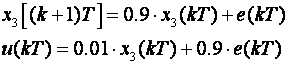
Pridružimo li ove jednadžbe prethodnima dobivamo jednadžbu tipa (3.5.38):
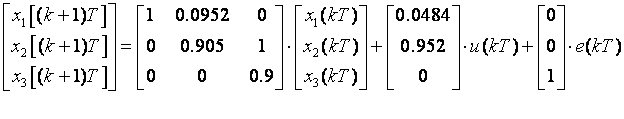
Sa slike vidimo da vrijedi
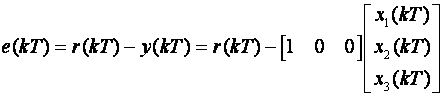
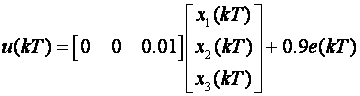
Iz svih ovih jednadžbi možemo izvući
Ostaje samo uvrstiti vrijednosti u jednadžbu (3.5.38). Konačni je rezultat
Slika 3.5.10 uspoređuje odziv zatvorenog regulacijskog sustava modeliranog jednadžbama stanja i sustava modeliranog impulsnim prijenosnim funkcijama prema slici 3.5.9. U trenucima uzorkovanja odzivi se u potpunosti podudaraju.
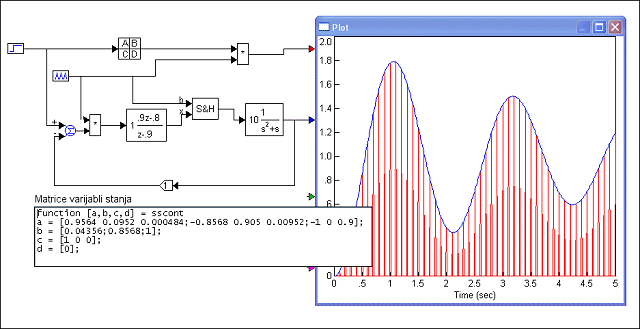
Slika 3.5.10. Simulacija sustava sa slike 3.5.9 i istog sustava opisanog jednadžbama varijabli stanja zatvorenog sustava za T=0.1 (varijable_stanja_zatvoreni.vsm)
Varijablama stanja ćemo se vratiti u poglavlju o projektiranju diskretnih sustava. Ukoliko postoji mogućnost uvida u varijable stanja sustava moguće je realizirati diskretno vođenje posebnih svojstava. Pri tome će nam osim osnovnih znanja o varijablama stanja trebati i znanje o analizi sustava opisanih varijablama stanja, prije svega stabilnost i osmotrivost, o čemu među ostalim govorimo u sljedećem poglavlju.