5.5.  Postupci vođenja temeljeni na varijablama stanja

Diskretnim vođenjem temeljenim na povratnoj vezi varijabli stanja vođeni sustav dobiva potpuno novu kategoriju. Moguće je postići cijeli niz novih svojstava, a neka od njih se ne bi mogla ni realizirati bez povratne veze varijabli stanja. U ovom ćemo poglavlju prikazati osnovne postupke diskretnog vođenja temeljenog na povratnoj vezi varijabli stanja od postupka postavljanja vlastitih vrijednosti matrice sustava što je identično postupku postavljanja polova impulsne prijenosne funkcije zatvorene petlje, pa do postupka optimalnog vođenja.

Povratnu vezu po varijablama stanja ne smijemo miješati s opisom zatvorenog regulacijskog sustava varijablama stanja o kojem smo govorili u poglavlju 3.5.6. Kod opisa zatvorenog regulacijskog sustava varijablama stanja regulator je bio uobičajeni, serijski regulator kome je ulaz bila pogreška, a izlaz upravljački signal. Radilo se samo o proširenju opisa sustava koji se vodi dodatnim jednadžbama varijabli stanja koje su opisivale serijski regulator. Kod vođenja povratnom vezom varijabli stanja upravljački se signal u(kT) temelji na razlici referentnog signala r(kT) i produkta matrice koeficijenata K i varijabli stanja u istom trenutku x(kT). Pogledajmo to detaljnije.

Za linearne diskretne, vremenski nepromjenjive sustave jednadžbe varijabli stanja glase:

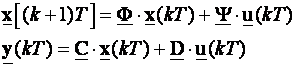          (5.5.1)

gdje prva jednadžba predstavlja jednadžbu stanja, a druga jednadžbu izlaza. Uvedimo povratnu vezu po varijablama stanja u obliku

          (5.5.2)

gdje je K matrica koeficijenata povratne veze po varijablama stanja, a r(kT) vektor referentnih ulaznih vrijednosti. Nakon uvrštavanja jednadžba varijabli stanja glasi:

          (5.5.3)

Grafički je prikaz dan na slici 5.5.1.

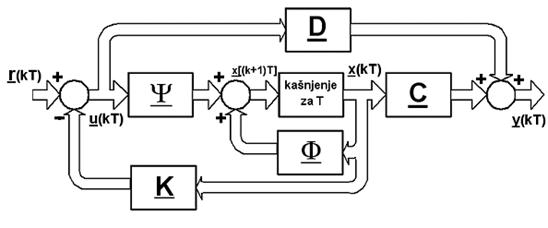
Slika 5.5.1. Diskretni sustav s povratnom vezom varijabli stanja

Da bi se vođenje povratnom vezom varijablama stanja moglo realizirati vođeni sustav treba biti dohvatljiv (Napomena: Prisjetimo se postoje pojmovi dohvatljivosti i upravljivosti koji u općem slučaju nisu istovjetni, sustav može biti upravljiv, ali ne dohvatljiv. Međutim u slučajevima kada se matrica sustava Φ može invertirati pojmovi su ekvivalentni, upravljiv sustav je dohvatljiv i obrnuto. Više detalja u poglavlju 4.7.3).

Isto tako sve varijable stanja x(kT) trebaju dostupne, mjerljive. Ukoliko to nije slučaj treba se uvesti osmatrač ili opserver pomoću kojega odredimo (estimiramo) vrijednosti varijabli stanja isključivo na temelju vektora izlaza y(kT). Vođeni sustav u tom slučaju treba biti osmotriv. O tome ćemo govoriti u posebnom poglavlju.