3.5.8. Prijelaz iz jednog opisa varijablama stanja u drugi opis i modalna forma
Ukoliko nam je poznat opis diskretnog sustava varijablama stanja, uvijek možemo preći i u drugi opis (za neki drugačiji izbor varijabli stanja) ukoliko se može definirati ne-singularna transformacijska matrica T. Pretpostavimo da je postojeći vektor varijabli stanja x(kT), da je novi vektor varijabli stanja w(kT), te da je moguće pronaći ne-singularnu transformacijsku matricu T tako da je zadovoljena matrična jednadžba:
![]() (3.5.44)
(3.5.44)
Postojeći opis ponašanja sustava varijablama stanja je
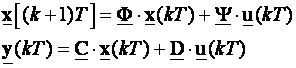 (3.5.45)
(3.5.45)
a do novog opisa dolazimo jednadžbom:
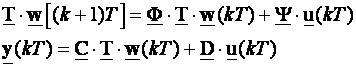 (3.5.46)
(3.5.46)
iz čega slijedi:
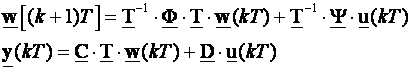 (3.5.47)
(3.5.47)
Vrlo važan pojam je i modalna ili dijagonalna realizacija diskretnog sustava varijablama stanja. Temelji se na modalnoj matrici transformacije P pomoću koje se sustav (3.5.45) prebacuje u oblik:
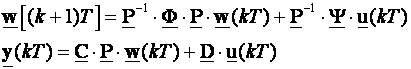 (3.5.48)
(3.5.48)
kod kojeg je matrica
![]() dijagonalna matrica kod koje se na dijagonali nalaze
vlastite ili karakteristične vrijednosti matrice
Φ .
dijagonalna matrica kod koje se na dijagonali nalaze
vlastite ili karakteristične vrijednosti matrice
Φ .
Ukoliko su sve karakteristične vrijednosti matrice Φ realne i jednake λ1 do λn modalna realizacija je oblika
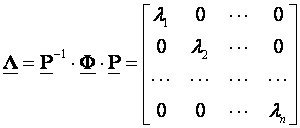 (3.5.49)
(3.5.49)
Ukoliko su neke od karakterističnih vrijednosti konjugirano kompleksne onda je primjereniji oblik:
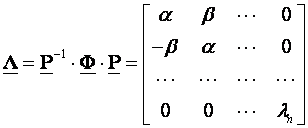 (3.5.50)
(3.5.50)
kod kojeg su a i b realni i imaginarni dio konjugirano kompleksne vlastite vrijednosti λ1=α+jβ i λ2=α-jβ.
Pogledajmo primjer istosmjernog motora upravljanog strujom armature prikazanog na slici 3.5.11.
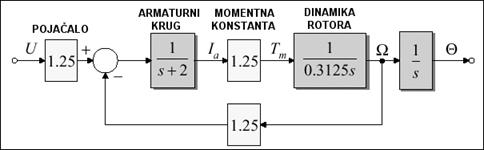
Slika 3.5.11. Blok shema istosmjernog motora i pojačala
Jednadžbe varijabli stanja su:
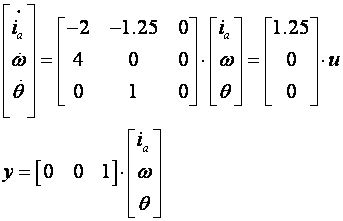
Uz T=0.1 diskretne jednadžbe varijabli stanja su
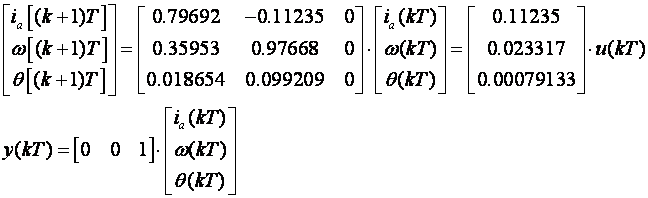
Vlastite vrijednosti matrice F su
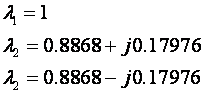
pa je modalna forma diskretnih varijabli stanja
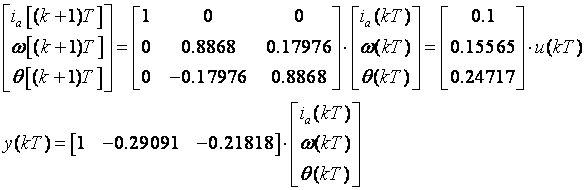
a modalna matrica transformacije
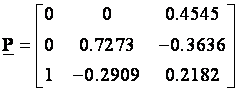
Napomena: Sve su vrijednosti izračunate programom Matlab koji ima odgovarajuće funkcije za prijelaz na modalnu formu i određivanje modalne matrice transformacija.