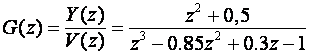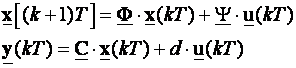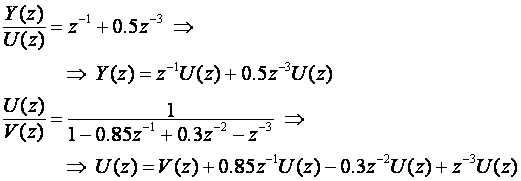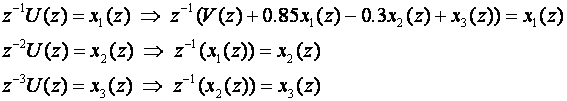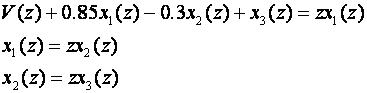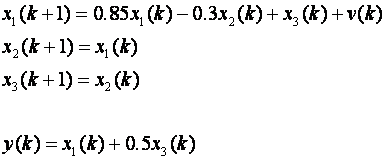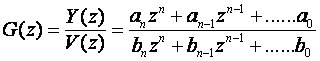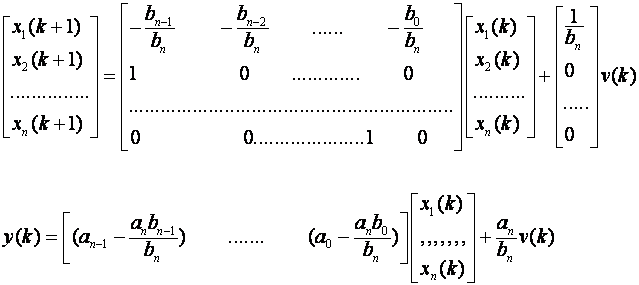3.5.9. Zadaci
1. Impulsna prijenosna funkcija i zapis u diskretnom prostoru stanja
Prostor stanja koji opisuje odnos diskretnih veličina prikazan je nizom jednadžbi diferencija i vrijedi općenito za sustave s jednim izlazom i jednim ulazom:
gdje su za sustave s jednim izlazom i jednim ulazom:
- x[(k+1)T] i x(kT) uzorci vektora stanja sustava u (k+1)T i kT trenutku
- vektor stanja je stupčasti vektor (n x 1) - reda
- Φ je konstantna, simetrična matrica sustava, (n x n) – reda
- ψ je konstantni stupčasti vektor (n x 1) – reda
- C je konstantni jednoredni vektor (1 x n) – reda
- d je konstanta
- v(k) su uzorci ulaznog signala u kT trenutku
- y(k) su uzorci izlaznog signala u kT trenutku
Ako je impulsna prijenosna funkcija iz koje treba dobiti matematički opis u prostoru stanja zadana pomoću polinoma višeg reda u brojniku i nazivniku, za rješavanje zadatka pomoći će pretvorba i relacije dobivene u Zadatku 3, poglavlje 3.4.8.
Dobili smo:
Uvedimo zapis:
Tada vrijedi i
Nove relacije mogu se zapisati i kao:
Iz ovog oblika jednostavno se prelazi u diskretno vremensko područje ili u jednadžbe diferencija:
Ako sve prikaženo u vektor-matričnom obliku, potvrdit ćemo da je dobiveni zapis prostor stanja.
Općenito!
Brojnik i nazivnik impulsne prijenosne funkcije su istog reda:
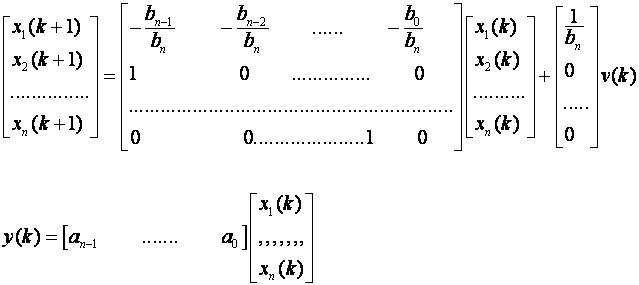
Pripadni zapis u prostoru stanja je:
Ako je stupanj brojnika manji od stupnja nazivnika (an = 0), mijenja se samo jednadžba izlaza i vrijedi: