Ekvivalentni povratni regulator varijabli stanja
Ekvivalentni povratni regulator smo spominjali već dva puta. On uključuje i procjenitelja stanja i povratnu vezu varijabli stanja. Polazna jednadžba u proračunu ekvivalentnog regulatora je bila:
![]() (5.5.56)
(5.5.56)
u kojoj smo u(kT) zamijenili s:
![]() (5.5.57)
(5.5.57)
te dobili opis procjenitelja stanja i regulatora:
 (5.5.58)
(5.5.58)
Ulaz u ekvivalentni povratni regulator je y(kT), a izlaz u(kT), pa možemo izvesti i njegovu impulsnu prijenosnu funkciju prema postupku iz poglavlja 3.5.4):
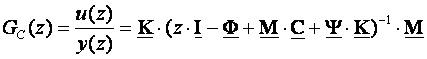 (5.5.59)
(5.5.59)
Kod proračuna ekvivalentnog povratnog regulatora može se koristiti Octave funkcija ss2tf(a,b,c,d) kojom se prelazi iz opisa varijablama stanja u prijenosnu funkciju. Pretvorba se temelji na standardnoj jednadžbi prelaska iz varijabli stanja u prijenosnu funkciju oblika (3.5.26):
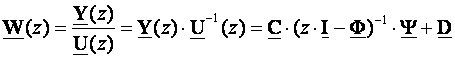 (3.5.26)
(3.5.26)
U funkciji ss2tf(a,b,c,d) stavljamo a = F , b = Y , c = C i d = D. Kod ekvivalentnog povratnog regulatora jednadžba prijelaza je (5.5.59), trebamo promijeniti argumente tako da bude a=F-M*C-Y*K, b=M, c=K i d=D. Funkcija kao rezultat daje polinom brojnika (num) i nazivnika (den) te se poziva u obliku: [num,den]=ss2tf(a,b,c,d).
U programskom jeziku Matlab postoji slična naredba [NUM,DEN] = SS2TF(A,B,C,D,iu). Razlika je jedino u varijabli 'iu' kojom se definira ulaz za koji se računa prijenosna funkcija.
Međutim kod Matlaba je proračun ekvivalentnog povratnog regulatora još i lakši zato što postoji funkcija reg(Gp,K,M,sensors,known,controls) gdje je Gp vođeni sustav opisan varijablama stanja kojeg u Matlabu računamo funkcijom ss - Gp = ss(Fi,Psi,c,d,T), K je vektor povratne veze varijabli stanja, M je matrica estimatora, a sensors,known,controls definiraju ulazno / izlazni podskup (koji je izlaz dostupan i na koji se upravljački ulaz djeluje).
Slično je i kod Scilaba kod kojeg postoji funkcija obscont(P,Kc,Kf)gdje je P sustav opisan varijablama stanja (koji se u Scilabu definira funkcijom syslin(d,Fi,Psi,c,d,[x0]) gdje d stoji kao oznaka da se radi o diskretnom sustavu, Fi,Psi,c,d su matrice opisa varijablama stanja, a [x0] vektor početnih uvjeta), Kc je matrica povratne veze varijabli stanja, a Kf matrica procjenitelja stanja.
Pogledajmo primjer:
Analizirati ćemo sustav trećeg reda čije su diskretne jednadžbe varijabli stanja:
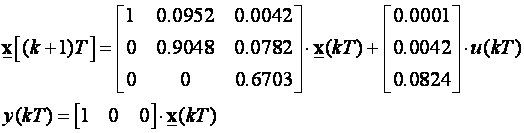
Za T=0.1 ovaj diskretni sustavu odgovara kontinuiranom sustavu:
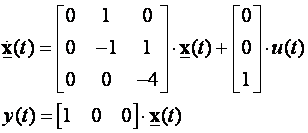
kojeg prikazujemo prijenosnom funkcijom
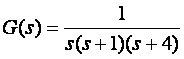
odnosno blok prikazom sa slike 5.5.29.
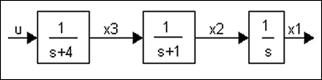
Slika 5.5.29. Vođeni sustav trećeg reda
Korijene procjenitelja stanja postaviti ćemo tako da vrijeme smirivanja procjenitelja stanja na 1% vrijednosti T1% od 0.5 sekundi, a da odziv procjenitelja odgovara odzivima Besselovog polinoma trećeg reda. Iz tablice na slici 5.5.4 uzimamo pol normaliziranog Besselovog polinoma trećeg reda B3(s): p1= -5.0093, p2 = -3.9668+j 3.7845 i p3 = -3.9668 - j 3.7845. Za 0.5 sekundi vrijednosti trebamo podijeliti sa 0.5: p1 = -5.0093/0.5= - 10.0186, p2 = -3.9668/0.5 +j 3.7845/0.5 = -7.9336 + j 7.569 i p3 = -7.9336 - j 7.569. U z području za T=0.1 imamo p01 = 0.3672, p02 = 0.328824 + j 0.310595 i p03 =0.328824 - j 0.310595.
Željeni polinom vođenog sustava potreban za proračun povratne veze varijabli stanja također računamo preko Besselovih polinoma tako da vrijeme smirivanja zatvorenog sustava bude 2 sekunde. Sustav je trećeg reda pa su normalizirani Besselovi polovi Besselovog polinoma B3(s) isti kao gore: p1 = -5.0093, p2 = -3.9668+j 3.7845, p3 = -3.9668-j 3.7845. Za vrijeme smirivanja T1% od 2 sekunde računamo: p1 = -5.0093/2=-2.50465, p2 = -3.9668+j 3.7845=-1.9834+j1.89225, p3 = -3.9668-j 3.7845=-1.9834-j1.89225. Za T=0.1 u z području imamo z1 = 0.7784, z2 = 0.8055+j0.1543, z3 = 0.8055-j0.1543.
Vektor procjenitelja stanja M i matricu povratne veze varijabli stanja računamo on-line verzijom programa Octave:
Rezultati su:
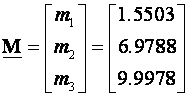
![]()
num =
1.0e+02 *
1.23572 -1.86376 0.68855
den =
1.00000 -0.83915 0.46666 -0.05431
što daje impulsnu prijenosnu funkciju ekvivalentnog regulatora:
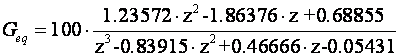
Slika 5.5.30 uspoređuje odzive varijabli stanja sustava vođenog povratnom vezom po varijablama stanja za diskretni model sustava bez procjenitelja stanja (varijable stanja su mjerljive) i uz asimptotski potpuni procjenitelj stanja za početne uvjete x(0)= [0 1 0]T. Uspoređuje se i rezultat dobiven modeliranjem procjenitelja stanja modelom varijabli stanja i združivanjem procjenitelja s povratnom vezom u ekvivalentni povratni regulator što smo ovdje detaljno analizirali. U odzivima također postoje male razlike zbog pojave algebarske petlje kod modeliranja procjenitelja stanja varijablama stanja.
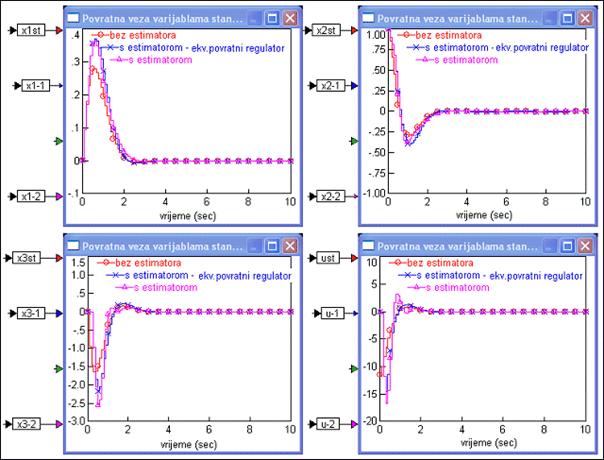
Slika 5.5.30. Usporedba odziva varijabli stanja sustava vođenog povratnom vezom po varijablama stanja bez procjenitelja stanja (ulaz u regulator su stvarne vrijednosti varijabli stanja) i s asimptotskim potpunim procjeniteljem stanja modeliranim varijablama stanja (krivulje xi-2) i združenim s povratnom vezom u ekvivalentni povratni regulator (krivulje xi-1) za početne uvjete x(0)= [0 1 0]T: a) varijabla stanja x1(kT), b) varijabla stanja x2(kT), c) varijabla stanja x3(kT), d) upravljanje u(kT) (varijable_stanja_estimatori_2.vsm)
Rezultati simulacije Matlabom prikazani su na slikama 5.5.31 i 5.5.32. Simulacija u Matlabu se provodi na temelju ekvivalentnog povratnog regulatora. Matlab program za gornji primjer može se pronaći na našem poslužitelju pod nazivom asimptotski_2.m. Slika 5.5.31 prikazuje vremenske promjene svih varijabli stanja sustava simuliranog diskretnim jednadžbama varijabli stanja. Posebno je zanimljiva slika 5.5.32 koja uspoređuje stvarne (simulirane) i procijenjene varijable stanja.
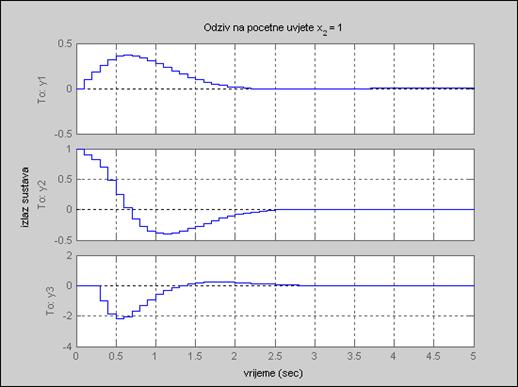
Slika 5.5.31. Varijable stanja sustava za početne uvjete x(0)= [0 1 0]T
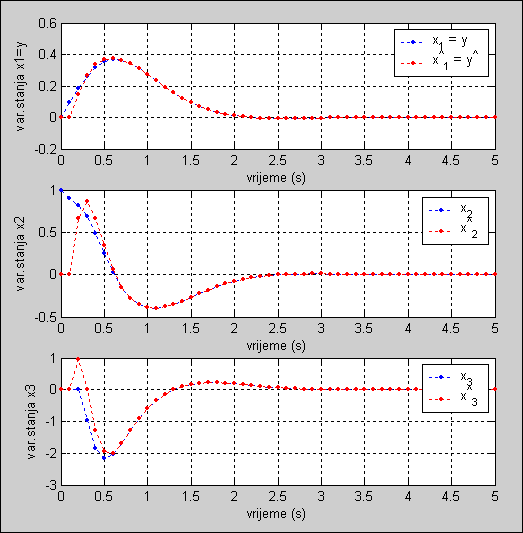
Slika 5.5.32. Usporedba stvarnih (simuliranih) i procijenjenih varijabli stanja. Razlika postoji zato što su početni uvjeti procjenitelja stanja jednaki nuli (asimptotski_2.m)
Početni uvjeti procjenitelja stanja
Razlike na slici 5.5.32 postoje zato što su početni uvjeti procjenitelja stanja bili različiti od početnih uvjeta sustava koji se vodi. Ukoliko početne uvjete procjenitelja stanja stavimo jednake početnim uvjetima sustava razlika neće postojat. Problem je u tome što nam varijable stanja sustava nisu dostupne, pa ne možemo odrediti niti njihove početne uvjete. Dostupne su nam jedino izlazne veličine sustava y(kT). Varijable stanja i izlazne veličine su povezane jednadžbom:
![]() (5.5.60)
(5.5.60)
gdje je C matrica reda n x 1, a x(kT) vektor od n nepoznanica reda 1 x n. Nama su poznati (mjerljivi) izlazi u trenutku KT=0 - y(0), znamo matricu C a nepoznat nam je vektor početnih uvjeta x(0). Prema teoriji linearnih jednadžbi jednadžba tipa (5.5.60) ima beskonačno rješenja. Rješenje koje od svih rješenja ima minimalnu normu (eng. Min-norm Solution) proračunava se jednadžbom:
![]() (5.5.61)
(5.5.61)
(za detalje pogledati literaturu na primjer – R.J. Vaccaro, Digital Control – A State-Space Approach, McGraw Hill, 1995).
Međutim u gornjem primjeru ovo nam puno ne pomaže. Za početne uvjete x(0)= [0 1 0]T, vektor izlaznog signala je y(0)= [0 0 0]T zato što je matrica C bila C = [1 0 0]. Jednadžba (5.5.61) ima smisla samo onda kada varijable stanja koje su vezane s izlaznim signalom imaju početne vrijednosti.
Slijedno vođenje
Kako se matrica povratna veza varijabli stanja određuje potpuno neovisno od matrice procjenitelja stanja, prijelaz na slijedno vođenje je direktan. Može se primijeniti bilo koji postupak iz poglavlja 5.5.1.4 Slijedno vođenje povratnom vezom varijabli stanja s tim da se umjesto izmjerenih varijabli stanja koriste procijenjene varijable stanja.