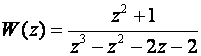3.5.4. Proračun impulsne
prijenosne funkcije uz poznate matrice varijabli stanja diskretnog sustava
Prebacimo jednadžbu izlaza u z područje
(3.5.24)
i uvrstimo X(z) proračunat u prethodnom poglavlju - jednadžba (3.5.19) uz nulte početne uvijete x(0) = 0
(3.5.25)
Dalje slijedi
(3.5.26)
Radi se o matričnoj impulsnoj prijenosnoj funkciji, kako imamo više ulaza i više izlaza. Na primjer za sustav s dva ulaza u1 i u2 i dva izlaza y1 i y2 matrična impulsna prijenosna funkcija je:
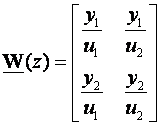(3.5.27)
i ona definira utjecaj svakog ulaza na svaki izlaz.
Primjer:
Za primjer iz poglavlja 3.5.2
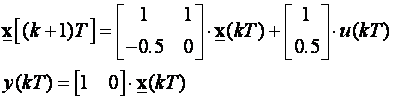
odredi impulsnu prijenosnu funkciju.
U ovom primjeru imamo samo jedan ulaz i jedan izlaz pa je matrična impulsna prijenosna funkcija reda 1 x 1:
Odzivi sustava opisanog impulsnom prijenosnom funkcijom i jednadžbama varijabli stanja se u potpunosti poklapaju kako i prikazuje slika3.5.5.
Slika 3.5.5. Odzivi sustava opisanog impulsnom prijenosnom funkcijom i jednadžbama varijabli stanja (varijable_stanja_prelaz _u_impulsnu.vsm)
Jednadžba (3.5.26) je više od teorijskog značaja i pogodna za ručni proračun impulsne prijenosne funkcije zato što uključuje inverziju oblika (z.I - Φ)-1 koji sadrži varijablu z. Programi za računalo su obično pisani tako da mogu proračunati inverziju matrice brojeva. Ovdje nam može pomoći Fadeev algoritam koji rekurzivno proračunava koeficijente karakterističnog polinoma koristeći trag matrice (trag matrice je suma dijagonalnih elemenata matrice). Pri tome koristimo spoznaju da je inverzija matrice jednaka kvocijentu matrice kofaktora i determinante
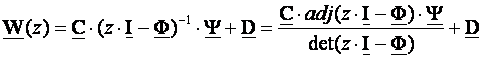(3.5.28)
Polovi od W(z) su jednaki korijenima det(z.I - Φ) a oni su određeni vlastitim vrijednostima matrice Φ. Fadeev algoritam daje:
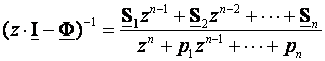(3.5.29)
gdje su:
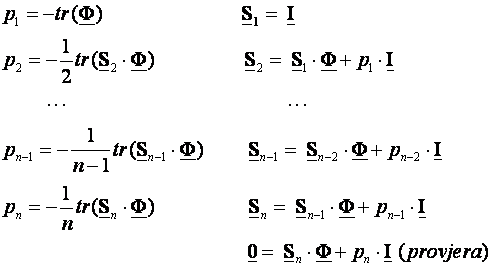(3.5.30)
Primjer:
Uzmimo sada primjer sustava trećeg reda:
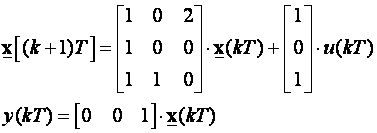
Impulsna prijenosna funkcija je prema (3.5.26) jednaka:
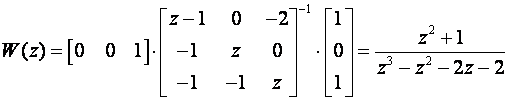
Provjerimo rezultat Fadeevim algoritmom:
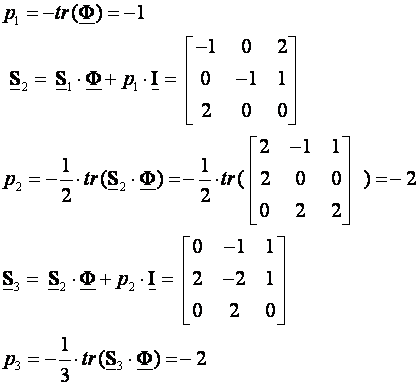
iz čega proračunavamo nazivnik prijenosne funkcije
Koeficijenti brojnika b1 do bn impulsne prijenosne funkcije jednaki su matričnom produktu:
što daje
pa je konačni rezultat:
