5.2.1. Postupak postavljanja polova i nula regulatora temeljen na GMK – geometrijskom mjestu korijena
Postupak je vrlo jednostavan i intuitivan. U z ravnini odredi se GMK sustava koji se želi voditi, a na temelju specifikacija željenog odziva sustava (vidi Definicije - Specifikacija odziva u vremenskom području i s ravnini) ucrta se i željeni položaj polova prijenosne funkcije zatvorenog sustava. Ukoliko GMK ne prolazi kroz ove točke z ravnine dodaju se polovi i nule diskretnog regulatora kojima ćemo GMK pomaknuti na način da prolazi kroz željene točke. Ovaj način projektiranja može se temeljiti na metodi pokušaja, ukoliko se koristi CAD programska podrška (npr. VisSim) i kroz nekoliko iteracija doći do željenog položaja pola regulatora, a može se regulator proračunati i analitički na isti način kako se računao kod kontinuiranih sustava. Regulator je najčešće oblika regulatora s faznim prethođenjem ili kašnjenjem:
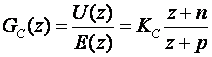(5.2.2)
a uobičajeno je da se nula regulatora postavi tako da poništi jedan od polova ekvivalentnog sustava ukoliko se radi o djelovanju na dinamička svojstva sustava, odnosno da se pol postavi što bliže točki z=1 ukoliko se radi o regulatoru koji utječe na pogreške ustaljenog stanja. Prilikom samog postupka projektiranja metodom pokušaja od velike su pomoći i krivulje konstantnog stupnja prigušenja i konstantne frekvencije neprigušenih oscilacija superponirane na GMK. Pomoću ove dvije veličine moguće je definirati željeno dinamičko ponašanje sustava.
Regulator tipa (5.2.2) često se naziva i kompenzator, a sustav u koji je on uključen kompenzirani sustav. Pogledajmo dva primjera. Prvi se odnosi na dodavanje regulatora sa faznim prethođenjem (PD tip), a drugi na dodavanje regulatora sa faznim kašnjenjem (PI tip).
Primjer:
Za sustav koji se sastoji od istosmjernog motora prijenosne funkcije Gm(s)=0.5/s(s+0.5) i pojačala prijenosne funkcije Gp(s)=K projektiraj regulator uz koji će vođeni sustav imati maksimalni prebačaj M=6.8% i vrijeme prvog maksimalnog prebačaja 0.65 sekunde. Period uzorkovanja je T=0.1.
Iz ovih specifikacija lako se izračuna (vidi Definicije – Specifikacija odziva u vremenskom području i s ravnini) željeni stupanj prigušenja ζ=0.65, ωp=4.77 rad/s i ωn=6.28 rad/s. Ove će specifikacije zadovoljavati sustav kojemu su u s ravnini dominantni polovi u točkama s1,2=-4.084±j4.77, odnosno u z ravnini za T=0.1 u točkama z1,2=0.591±j0.305.
Nacrtajmo najprije GMK sustava bez regulatora. Ekvivalentnu impulsnu prijenosno funkciju za sustav prijenosne funkcije oblika G(s)=K/s(Tms+1) računali smo u poglavlju 4.4.2 Nyquistovi frekvencijski dijagrami :
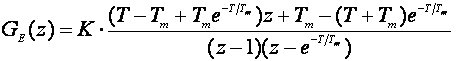
U našem je slučaju T=0.1 i Tm =2 pa imamo
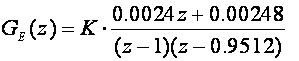
Slika 5.2.2 prikazuje GMK nekompenziranog sustava za promjenu pojačanja K od 0 do 200.
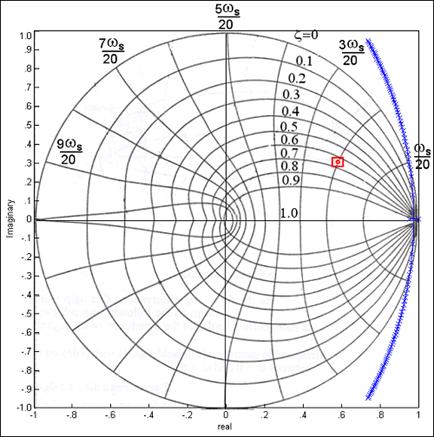
Slika 5.2.2. GMK nekompenziranog sustava unutar jedinične kružnice i položaj željenog pola impulsne prijenosne funkcije zatvorene petlje koji zadovoljava postavljene specifikacije
GMK ne prolazi kroz željenu točku. Što više sustav je vrlo blizu ruba stabilnosti i već uz male vrijednosti pojačanja K daje oscilatorni odziv.
Ideja kompenzacije je sljedeća: Poništiti pol sustava u točki z=0.9512 i dodati novi pol koji se nalazi bliže ishodištu. Na taj će se način cijeli GMK pomaknuti prema lijevoj strani. U nekoliko se pokušaja može pronaći položaj tog novog pola za kojeg će GMK prolaziti točno kroz željenu točku. Krećemo s polom u točki z=0.6. Impulsna prijenosna funkcija regulatora kojemu je Gc(z)=1 za z=1 je:
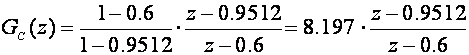
Kako je nula regulatora bliže točki z=1 radi se o regulatoru PD tipa (regulatoru s faznim prethođenjem). Impulsna prijenosna funkcija otvorenog kompenziranog sustava čiji GMK crtamo:
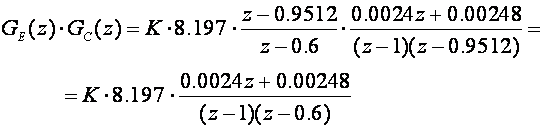
Slika 5.2.3 pokazuje GMK kompenziranog sustava.
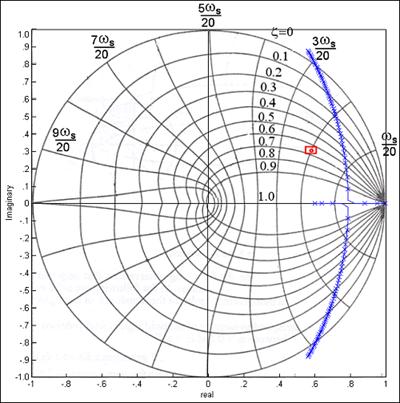
Slika 5.2.3. GMK kompenziranog sustava unutar jedinične kružnice i položaj željenog pola impulsne prijenosne funkcije zatvorene petlje koji zadovoljava postavljene specifikacije
GMK i dalje ne prolazi kroz željenu točku. Pomičemo pol još više lijevo u točku z=0.3. Impulsna prijenosna funkcija regulatora sada glasi:
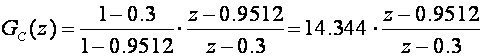
a impulsna prijenosna funkcija otvorenog kompenziranog sustava
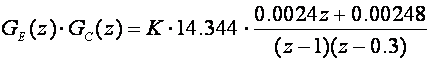
GMK prikazuje slika 5.2.4.
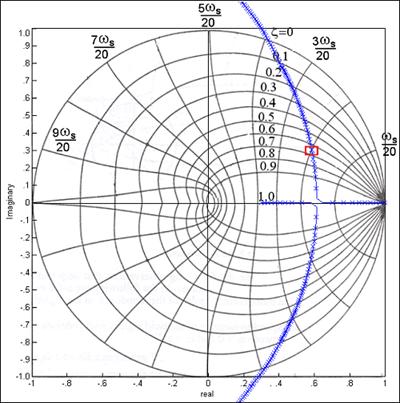
Slika 5.2.4. GMK kompenziranog sustava unutar jedinične kružnice i položaj željenog pola impulsne prijenosne funkcije zatvorene petlje koji zadovoljava postavljene specifikacije
GMK točno prolazi kroz željenu točku za K=4. Provjerimo sintezu simulacijom vođenog sustava. Rezultat je slika 5.2.5.
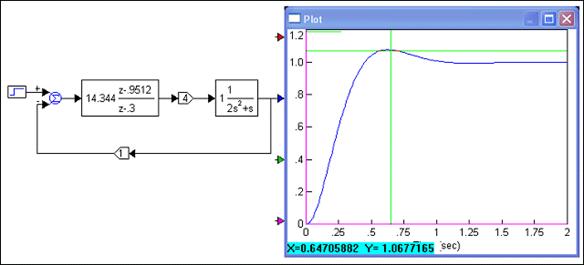
Slika 5.2.5. Odziv sustava vođenog diskretnim regulatorom dobivenim metodom pokušaja (sinteza-gmk.vsm)
Pokažimo kako se i analitički može doći do rezultata koji će bitu blizu rješenju dobivenom metodom pokušaja, ali zahtjeva računanje.
Željeni položaj pola u z ravnini je z1,2=0.591±j0.305, a impulsna prijenosna funkcija kompenziranog sustava s regulatorom općeg oblika:
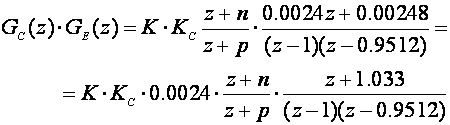
Nulom regulatora poništavamo pol sustava pa je n=0.9512 , a pol ćemo postaviti između z=0 i z=1 pa dobijemo
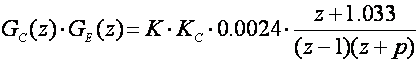
Položaj pola odredimo iz zahtjeva da kompenzirani sustav zadovoljava jednadžbu argumenta za K=0 (početni položaj polova i nula otvorene petlje). Slika 5.2.6. prikazuje položaje svih polova i nula za K=0.
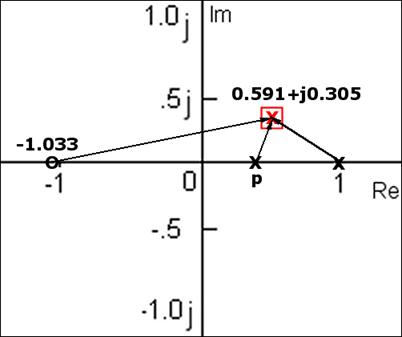
Slika 5.2.6. Položaj polova i nula otvorenog kompenziranog sustava
Argument pola u točki z=1 je 143.29o, a nula u točki z=-1.033 ima argument 10.63 o, pa u skladu s jednadžbom argumenta argument pola u točki p treba biti:
Sada je jednostavno izračunati položaj pola p:
a to je skoro ista vrijednost koju smo odredili i eksperimentalno. Analitički možemo izračunati i pojačanje. Jednadžba modula daje
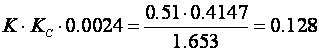
Pojačanje regulatora je
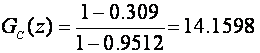
pa je potrebno pojačanje
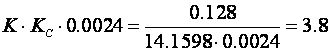
što je opet relativno blizu vrijednosti koju smo odredili simulacijama.
Slika 5.2.7 prikazuje odziv vođenog sustava. Prebačaj je nešto malo manji od specificiranog.
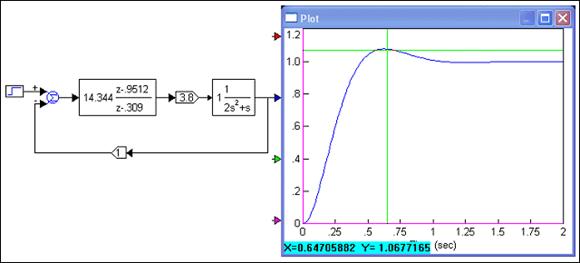
Slika 5.2.7. Odziv sustava vođenog diskretnim regulatorom dobivenim analitičkim proračunom (sinteza-gmk.vsm)
Na prethodnim slikama bio je prikazan samo dio GMK unutar jedinične kružnice. Cijeli GMK kompenziranog sustava s polom kompenzatora u točki z=0.3 dan je na slici 5.2.8. Na slici je ucrtana i jedinična kružnica. Sustav je stabilan samo za pojačanja unutar jedinične kružnice.
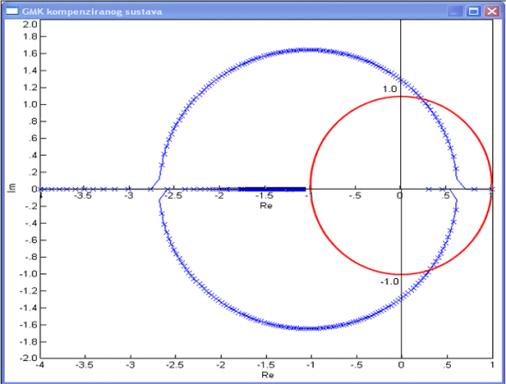
Slika 5.2.8. Cijeli GMK sustava s regulatorom PD tipa
U prethodnom je primjeru razmatran regulator s faznim prethođenjem (PD tipa) kojim se djeluje na poboljšanje dinamičkih svojstava sustava. Na sličan se način može projektirati i regulator s faznim kašnjenjem (PI tipa) kojim djelujemo na pogreške ustaljenog stanja. U njegovom proračunu GMK nam toliko i ne treba. Pomoću njega samo provjeravamo dinamička svojstva sustava.
Kod regulatora s faznim kašnjenjem pol je bliže točki z=1 i obično se postavlja što bliže točki z=1, a položaj nule se računa iz zahtjeva za iznos pogreške ustaljenog stanja.
Pogledajmo primjer projektiranja za sustav iz prethodnog primjera kojem je već dodan regulator s faznim prethođenjem.
Primjer:
Sustav s regulatorom iz prethodnog primjera ima impulsnu prijenosnu funkciju otvorene petlje
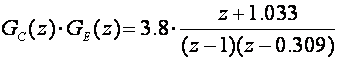
Sustav je prve vrsti pa nema pogrešku ustaljenog stanja položaja, ali ima pogrešku ustaljenog stanja brzine
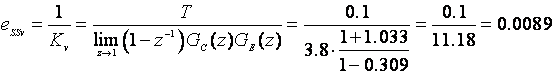
Pretpostavimo li da je želimo smanjiti na 0.005, tako konstanta pogreške brzine Kv treba iznositi 20 (Kv = T/eSSv = 0.1/0.005 = 20).
Regulator s faznim kašnjenjem ima impulsnu prijenosnu funkciju istog oblika kao i regulator s faznim prethođenjem s tim da je kod njega n<p:
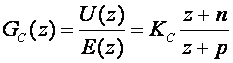
Pol se obično bira što bliže točki z=1, a za pojačanje regulatora se uzme KC = 1. Na primjer stavimo pol u točku z=0.98. Za početak pretpostavimo da novi regulator PI tipa neće doprinositi ukupnom pojačanju sustava, te da neće utjecati na dinamička svojstva vođenog sustava. Pretpostavljamo da će pol i nula PI regulatora biti blizu jedan drugome, pa će argumenti i moduli vektora od nule i pola regulatora do željenog pola zatvorenog sustava biti slični, te će doprinos pojačanja regulatora ukupnom pojačanju biti zanemariv. Da li će to biti istina vidjeti ćemo tek na kraju.
Konstanta pogreške brzine je sada
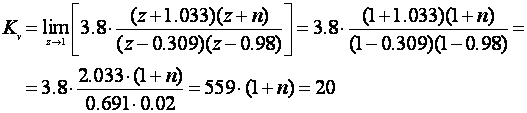
iz čega slijedi
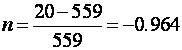
pa bi impulsna prijenosna funkcija regulatora s faznim kašnjenjem trebala biti
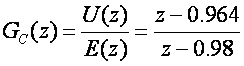
Slika 5.2.9. prikazuje povećani dio odziva sustava nakon smirenja za jediničnu pravčastu uzlaznu funkciju na kojem se dobro vidi smanjenje pogreške ustaljenog stanja brzine.
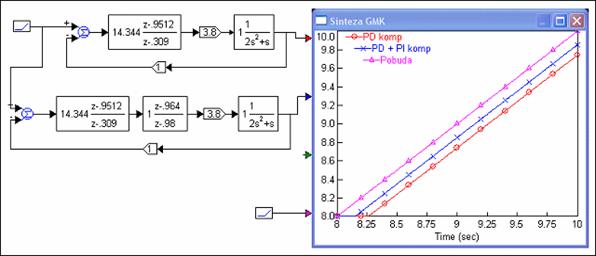
Slika 5.2.9. Usporedba odziva sustava bez regulatora i s regulatorom s faznim kašnjenjem (PI) za uzlazni ulazni signal (sinteza-gmk-2.vsm)
Iz odziva na jedinični skok vidi se da nam je početna pretpostavka o utjecaju ovog regulatora na jednadžbu modula i argumenata GMK bila u redu. Dinamička svojstva sustava kojem je dodan regulator nisu se bitno promijenila, što znači da GMK prolazi kroz istu točku koju smo zadali na početku prvog primjera.
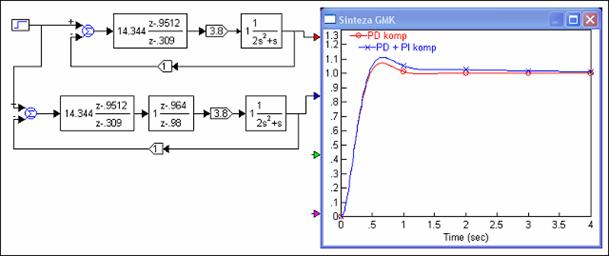
Slika 5.2.10. Usporedba odziva sustava bez regulatora i s regulatorom s faznim kašnjenjem (PI) za skokoviti ulazni signal (sinteza-gmk-2.vsm)
Na slici 5.2.11 superponirali smo GMK sustava s oba regulatora na GMK sustava samo s PD regulatorom iz prethodnog primjera. Oba se skoro poklapaju.
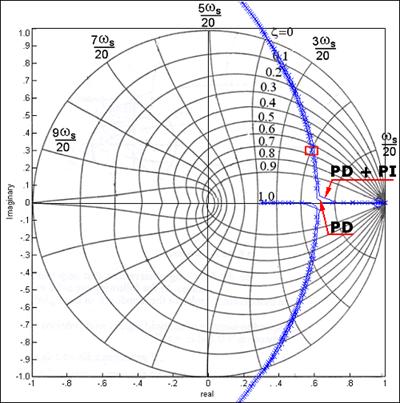
Slika 5.2.11. GMK sustava s PD regulatorom i sustava s PD i PI regulatorom