5.4. Projektiranje diskretnog regulatora u pseudo-frekvencijskom w području
Ovo je varijanta postupka projektiranja regulatora koja na neki način kombinira oba prije spomenuta postupka – i postupak sinteze regulatora u kontinuiranom području i postupak sinteze regulatora u diskretnom području. Sastoji se u tome da se model vođenog sustava prikaže diskretnim ekvivalentom, pa da se nakon toga na njega primjeni još jedna transformacija, ovaj put bilinearna te se on prebaci u w područje. Regulator se tu i proračuna koristeći na primjer Bodeove ili Nicholsove dijagrame, a konačni oblik regulatora se dobije vraćanjem natrag iz w područja u z područje, prebacivanjem GC(w) u GC(z).
Postavlja se pitanje ima li uopće smisla koristiti ovu metodu ukoliko smo u diskretno područje došli diskretizacijom kontinuiranog sustava koji se vodi. Sintezu temeljenu na Bodeovim dijagramima mogli smo odmah provesti u kontinuiranom području. U w području imamo dodatne probleme, na primjer frekvencije potpuno ne odgovaraju onima iz s područja (zato ih i zovemo pseudo-frekvencije) – vidi poglavlje o bilinearnoj transformaciji.
Međutim ukoliko smo u diskretno područje došli direktno, bez izvođenja kontinuirane prijenosne funkcije, postupak ima smisla. Iz z područja ne možemo jednoznačno preći u s područje, ali primjena bilinearne transformacije daje jednoznačno preslikavanje. Postupci sinteze koji se na primjer temelje na Bodeovim dijagramima su izuzetno dobro razrađeni i daju intuitivni uvid u frekvencijske karakteristike budućeg sustava, a posebno u mjere relativne stabilnosti. Postupci su skoro identični onima iz kontinuiranog područja pa ćemo ih samo kratko spomenuti.
Možda je najznačajnije to što se regulator projektiran korištenjem Bodeovih dijagrama promatra kao filter. Sustav bez regulatora ima određenu frekvencijsku karakteristiku (amplitudnu i faznu). Zadane specifikacije definiraju izgled željene frekvencijske karakteristike. Ne zaboravimo da su frekvencijski i vremenski prikaz izlaznog signala samo dva različita načina prikazivanja iste pojave. U dijelu u kojem govorimo o specifikacijama odziva u vremenskom i kompleksnom području i frekvencijskom području to je i naglašeno. Ukoliko se ove dvije frekvencijske karakteristike ne poklapaju unosimo regulator – filter kojim selektivno djelujemo na frekvencijsku karakteristiku sustava kako bismo pojačavanjem ili prigušivanjem određenih frekvencijskih komponenti dobili upravo onakvu karakteristiku kakvu zahtijevaju postavljene specifikacije.
Na primjer odziv nam ne zadovoljava u početnom dijelu. Hoćemo ga ubrzati. Vrijeme i frekvencija su obrnuto proporcionalni, pa je početno vrijeme vezano s visokim frekvencijama. Odziv možemo ubrzati ukoliko selektivno pojačamo visoke frekvencije. Naravno pri tome trebamo imati na umu da su i smetnje obično na visokim frekvencijama, pa ne smijemo pretjerati. Regulator koji radi upravo to – pojačava visoke frekvencije, a ne djeluje na niskim frekvencijama je regulator PD tipa.
Slično možemo razmišljati i o regulatoru PI tipa koji treba smanjivati pogrešku ustaljenog stanja. Pogreška ustaljenog stanja vezana je s velikim vremenima, pa regulator treba biti djelotvoran na niskim frekvencijama. Naravno ovo je grubo, kvalitativno objašnjenje, ali dostatno da shvatimo kako je regulator samo posebno projektiran filter.
Prvi korak postupka projektiranja je prijelaz iz z područja u w područje primjenom bilinearne transformacije. Prebacujemo sustav koji trebamo voditi. U poglavlju 4.4.1 spomenuli smo dva tipa bilinearne transformacije: Möbiusovu bilinearnu transformaciju kod koje se z zamjenjuje sa:
(5.4.1)
i Tustinovu bilinearnu transformaciju koja vjernije povezuje frekvencije iz w područja i s područja (bar za male vrijednosti ωT/2), ali je zato nepraktična za računanje:
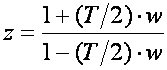(5.4.2)
Sljedeći je korak crtanje Bodeovih dijagrama funkcije G(w) i provjera da li sustav zadovoljava postavljene specifikacije. One se obično zadaju ili preko željene fazne ili amplitudne pričuve ili preko željenog pojasa propuštanja. Sjetimo se da je pojas propuštanja za sustav drugog reda ovisan o stupnju prigušenja sustava i neprigušenoj frekvenciji. Što je stupanj prigušenja veći to je pojas propuštanja manji, a što je neprigušena frekvencija veća to je i pojas propuštanja veći.
Ukoliko sustav ne zadovoljava ubacujemo odgovarajući regulator. Obično se ubacuje dipolni regulator s faznim prethođenjem ili kašnjenjem. Regulator se obično odabire iskustveno po principu 'pokušaj i pogriješi' pa se zato ovim postupkom nećemo detaljno baviti. Samo ćemo ga ilustrirati primjerom vođenja istosmjernog motora.
Primjer:
Impulsna ekvivalentna prijenosna funkcija istosmjernog motora kojem smo zanemarili trenje u ležajevima i induktivitet namota je za T=0.1:
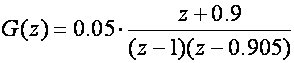
Proračunajmo regulator tako da vođeni sustav ima faznu pričuvu najmanje 50o .
Napomena: Ovoj impulsnoj prijenosnoj funkciji u kontinuiranom području odgovara prijenosna funkcija G(s)=10/s(s+1), ali to u ovom trenu nije bitno. Pretpostavljamo da smo do ekvivalentne impulsne prijenosne funkcije došli eksperimentom.
Prebacimo se najprije u w područje:
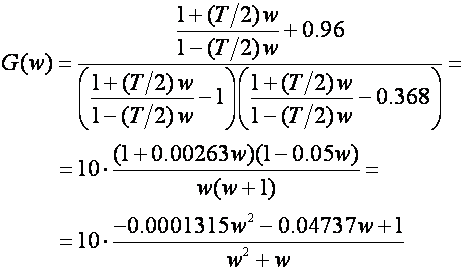
Slika 5.4.1 prikazuje frekvencijske dijagrame sustava nekompenziranog sustava
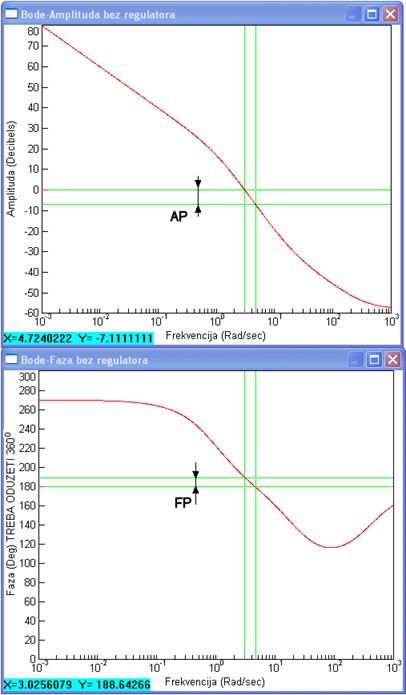
Slika 5.4.1. Frekvencijski dijagrami nekompenziranog sustava u w području (sinteza-w-podrucje.vsm)
Kako impulsna prijenosna funkcija ima jedan član ne-minimalne faze u w području vrijednosti faznog kuta su povećane za 360o (za detalje vidi poglavlje o Bodeovim dijagramima). Sa slike čitamo vπ=4.7 rad/s, AP = - (-7.1 dB) =7.1 dB, vI=3.0 rad/s i FP =188.6o –360o +180o = 8.6o. Zanima li nas stvarna frekvencija kritične faze dobijemo je iz jednadžbe ωπ=arctg(4.7)=1.36 rad/s.
Naš je zahtjev fazna pričuva najmanje 50o. Ubacujemo regulator s faznim prethođenjem oblika GC(z)=Kc(z-a)/(z+0.5). Izbor nule regulatora temelji se obično na postupku 'pokušaj-i-pogriješi', a pojačanje Kc se računa tako da za z=1 ukupno pojačanje regulatora bude 1. Na primjer krenemo s regulatorom:
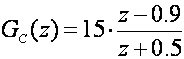
Kc =(1+0.5)/(1-0.9)= 15
U w području njegova prijenosna funkcija regulatora glasi
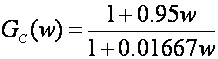
Slika 5.4.2 prikazuje Bodeove dijagrame kompenziranog sustava.
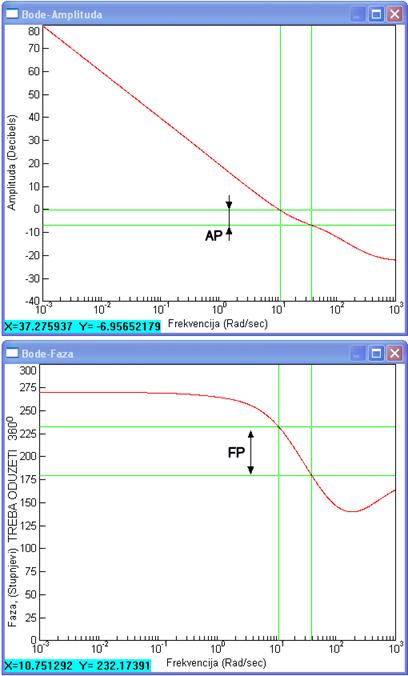
Slika 5.4.2. Frekvencijski dijagrami kompenziranog sustava u w području (sinteza-w-podrucje2.vsm)
Sa slike čitamo vπ=37.3 rad/s, AP = - (-6.9 dB) = 6.9 dB, vI=10.8 rad/s i FP = 232.2o – 360o + 180o = 52.2o. Zahtjev za faznom pričuvom je prema tome zadovoljen.
Zanimljivo je pogledati faznu karakteristiku samog regulatora (kompenzatora). Prikazuje ga slika 5.4.3.
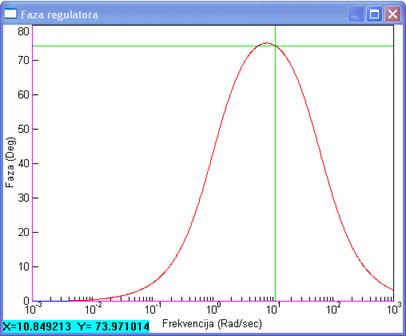
Slika 5.4.3. Fazni dijagram regulatora GC(w)=(1+0.95w)/(1+0.01667w)
Na frekvenciji vI=10.8 rad/s njegov fazni doprinos je oko 74o. Provjerimo fazu sustava bez regulatora na toj frekvenciji. Prikazuje je slika 5.4.4.
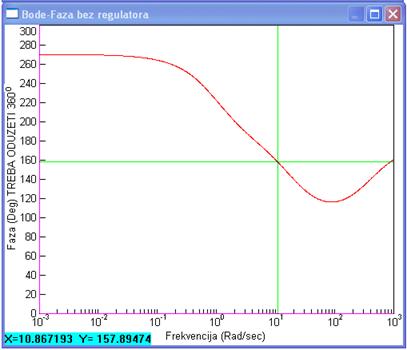
Slika 5.4.4. Fazni dijagram sustava bez regulatora i vrijednost faze na frekvenciji vI=10.8 rad/s
Faza sustava bez vođenja na frekvenciji vI=10.8 rad/s je 158o – 360o = – 202o, a fazna pričuva FP= – 202o + 180 = –22o. Dodamo li tome doprinos kompenzatora od 74o rezultantna fazna pričuva je 74o –22o =52o, a to je upravo koliko smo i željeli.
Slika 5.4.5 prikazuje vremenski odziv nekompenziranog i kompenziranog sustava.
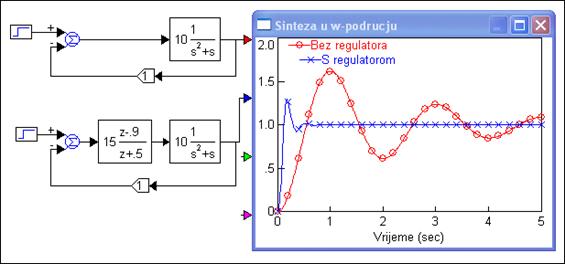
Slika 5.4.5. Vremenski odziv nekompenziranog i kompenziranog sustava (sinteza-w-podrucje2.vsm)
Uzmimo sada za primjer regulator:
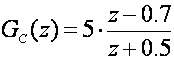
U w području njegova prijenosna funkcija regulatora glasi
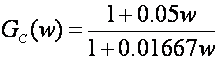
Slika 5.4.6 prikazuje Bodeove dijagrame kompenziranog sustava.
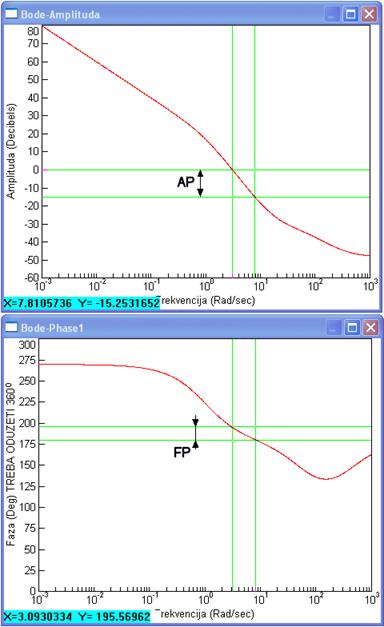
Slika 5.4.6. Frekvencijski dijagrami kompenziranog sustava u w području (sinteza-w-podrucje3.vsm)
Sa slike čitamo vπ=7.8 rad/s, AP = - (-15.2 dB) = 15.2 dB, vI=3.1 rad/s i FP = 195.6o – 360o + 180o = 15.6o. Očito nedovoljno. Zanimljivo je pogledati i vremenski odziv sustava s regulatorom i usporediti ga sa prethodnim. Slika 5.4.7 to prikazuje.
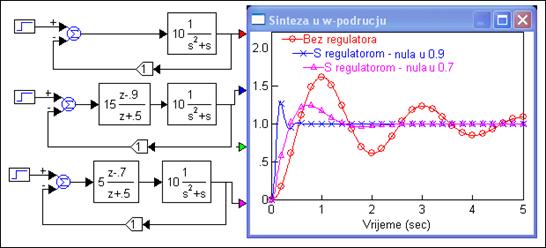
Slika 5.4.7. Vremenski odziv nekompenziranog i kompenziranih sustava (sinteza-w-podrucje3.vsm)
U ovom je slučaju i odziv sporiji.
Smanjimo li za prvi regulator pojačanje s 15 na 10 odziv sustava će biti još bolji i prikazuje ga slika 5.4.8.
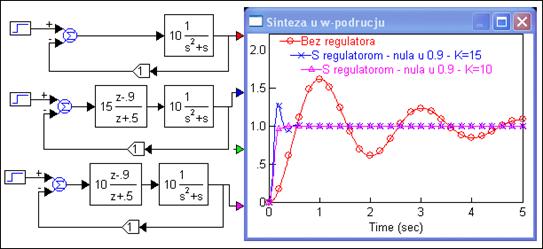
Slika 5.4.8. Vremenski odziv sustava s regulatorom GC(z)=10(z-0.9)/(z+0.5) (sinteza-w-podrucje4.vsm)
Pri tome se fazna pričuva čak povećala. Frekvencijske dijagrame kompenziranog sustava prikazuje slika 5.4.9.
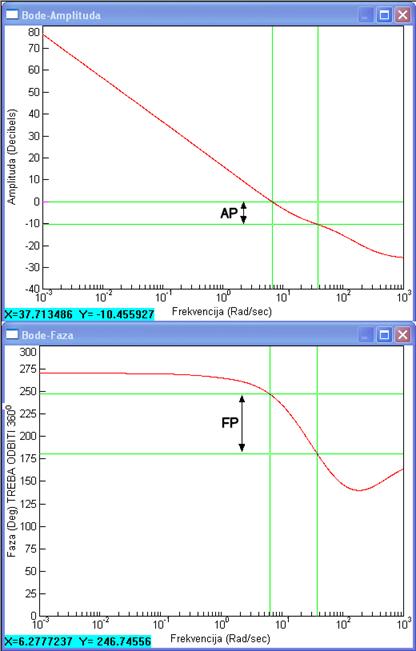
Slika 5.4.9. Frekvencijski dijagrami sustava s regulatorom GC(z)=10(z-0.9)/(z+0.5) (sinteza-w-podrucje4.vsm)
Sa slike čitamo vπ=37.7 rad/s, AP = - (-10.5 dB) = 10.5 dB, vI=6.3 rad/s i FP = 246.7o – 360o + 180o = 66.7o. Kako po teoriji automatske regulacije uvijek moramo nešto izgubiti, ukoliko smo nešto dobili, u ovom slučaju je to pogreška ustaljenog stanja brzine. Za K=15 iznosila je eSSv=0.1, a za K=10 eSSv=0.15.
Rezultat svih postupaka projektiranja diskretnog regulatora koje smo do sada spomenuli je impulsna prijenosna funkcija regulatora GC(z). Želimo li diskretni regulator primijeniti kao digitalni regulator potreban nam je oblik prilagođen programiranju i radu digitalnog računala. To je jednadžba diferencija koja daje vrijednost upravljačkog signala u trenutku kT kao funkciju prošlih upravljačkih signala i prošlih vrijednosti pogreške sustava. Proces kojim se impulsna prijenosna funkcija prebacuje u jednadžbu diferencija naziva se realizacija impulsne prijenosne funkcije i o njemu detaljno govorimo u poglavlju 6.1.