2.2.1. Uzorkovanje
Postupak diskretizacije po vremenu koji nazivamo uzorkovanje (eng. sampling) možemo definirati kao postupak prikaza kontinuiranog signala slijedom brojeva koji predstavljaju vrijednost signala u pojedinim trenucima vremena.
Uzorkovanje je temeljni postupak digitalnog vođenja, prije svega zbog toga što i sama računala rade u diskretnom taktu, pa je dobro razumijevanje procesa uzorkovanja od posebne važnosti. Krenimo s matematičkim opisom postupka uzorkovanja:
Neka je ![]() skup pozitivnih i negativnih cijelih brojeva
skup pozitivnih i negativnih cijelih brojeva ![]() i neka je
i neka je ![]() podskup
skupa realnih brojeva
podskup
skupa realnih brojeva ![]() koji ćemo nazvati skup trenutaka uzorkovanja. Uzorkovanje je
linearna operacija:
koji ćemo nazvati skup trenutaka uzorkovanja. Uzorkovanje je
linearna operacija:
gdje T nazivamo period uzorkovanja (prisjetimo se da ovdje analiziramo samo regularnu kvantizaciju po vremenu). Izraz fs= 1/T nazivamo frekvencija uzorkovanja, a ωs=2π fs =2π/T kružna frekvencija uzorkovanja.
Sklop u kojem se uzorkovanje provodi nazivamo sklop za uzorkovanje ili uzorkivač, a u inženjerskom žargonu često se naziva i "sampler" prema engleskoj riječi "sampling" koja znači uzorkovanje. Na shemama ga prikazujemo sklopkom uz koju je napisano slovo T što simbolizira njeno ritmičko otvaranje i zatvaranje u vremenskim intervalima perioda uzorkovanja (slika 2.2.3).
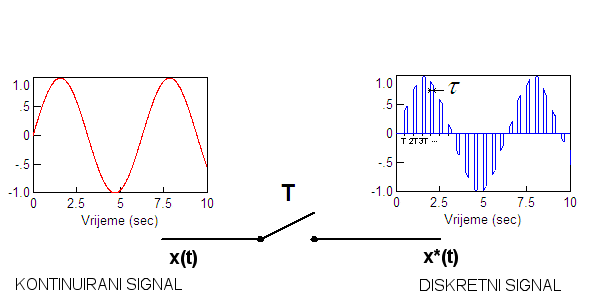
Sklopka ostaje uključena konačni period vremena τ.
Sklop za uzorkovanje možemo promatrati i kao
modulator, množač u kojem se množe dva signala:
- kontinuirani signal x(t) koji predstavlja signal koji modulira, i
- slijed impulsa jedinične amplitude u(T,τ) koji predstavlja signal koji se
modulira.
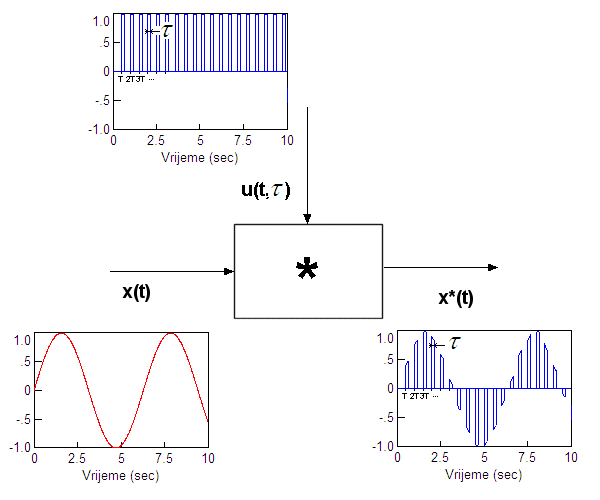
Slika 2.2.4. Sklop za uzorkovanje kao modulator
Izlazni signal
je signal diskretiziran po vremenu.
U praksi je najčešće ispunjen uvjet τ
<< T , pa se slijed jediničnih impulsa
prikazanih na slici 2.2.5 matematički zamjenjuje slijedom pomaknutih Diracovih
δ funkcija (eng. Pulse
Train) koje se simbolički označavaju sa δT a matematički izražavaju beskonačnim
redom:
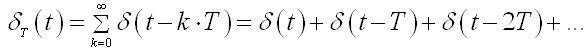
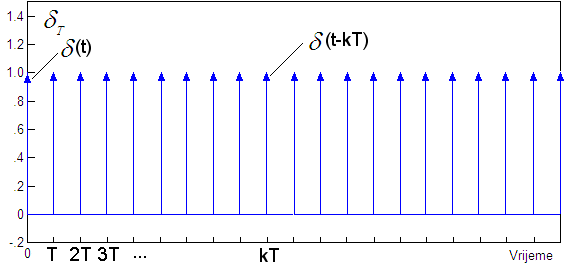
Slika 2.2.5.
Jednadžba (2.2.6) sada glasi:
Pretpostavimo sada da uzorkujemo čisti sinusni signal frekvencije ωo =2π/To i amplitude A: x(t) = A sin ωot.
Slika 2.2.6 prikazuje dvije situacije za različite odnose perioda
uzorkovanja T i periode kontinuiranog signala To.
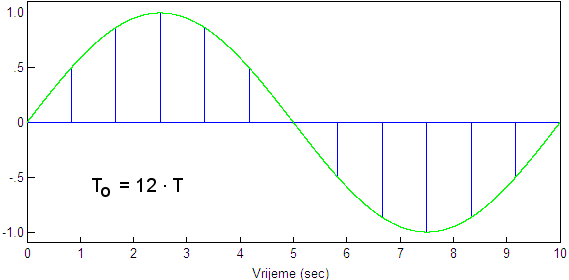
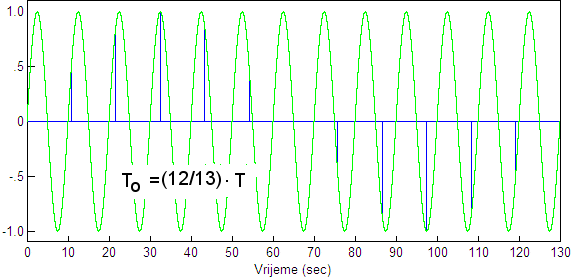
Slika 2.2.6. Uzorkovanje sinusnog signala za različite odnose perioda uzorkovanja T i periode sinusnog signala To: gornja slika - To=12T i donja slika - To=(12/13)T
Promatrajući sliku 2.2.6. pretpostavimo da nam je poznat samo diskretni signal na slikama označen plavo. U oba slučaja on je identičan iako smo uzorkovali dva potpuno različita sinusna signala. U prvom slučaju je to bio: x(t) = A sin (π/6T)t , a u drugom x(t) = A sin (13π/6T)t .
Kada bi nam netko zadao zadatak da iz diskretnog signala rekonstruiramo kontinuirani mi bi u oba slučaja pretpostavili da se radi o prvom signalu prikazanom na slici 2.2.6.
Napomena:Ovaj fenomen je poznat pod pojmom frekvencijsko preklapanje ili kako se često prema eng. riječi zove Aliasing i o njemu će biti više riječi u poglavlju 2.2.5 .
Sada se postavlja temeljno pitanje: Kakav mora biti odnos između frekvencije signala koji se uzorkuje i frekvencije uzorkovanja da bi se kontinuirani signal mogao (bar teorijski) u potpunosti rekonstruirati i vratiti u prvobitni kontinuirani oblik? Odgovora se prvi posjetio Nyquist 1928. godine o čemu više u sljedećem poglavlju.