2.2.2.  Teorem uzimanja uzoraka

Nyquist je 1928. godine napisao:

21 godinu kasnije (1949) C.E. Shannon je proširio Nyqvistova istraživanja na bilo kakve signale te postavio i matematički dokazao cjeloviti teorem uzimanja uzoraka (eng. Sampling Theorem). U originalu on glasi:

"Kontinuirani signal čiji su koeficijenti Fourierove transformacije jednaki nuli izvan intervala (- ω_o, ω_o) jedinstveno je određen svojim vrijednostima definiranim u jednako udaljenim trenucima vremena ukoliko je kružna frekvencija uzorkovanja veća od 2ω_o. Kontinuirani se signal x(t) može proračunati iz diskretnog signala x(kT) interpolacijskom formulom:

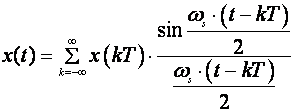
gdje je ω_s =2 π f_s =2 π / T  kružna frekvencija uzorkovanja."

Drugim riječima ukoliko kontinuirani signal sadrži frekvencije od 0 do maksimalno f_o Hz tada se on u potpunosti može rekonstruiran iz slijeda uniformno udaljenih diskretnih uzoraka koji se pojavljuju s frekvencijom uzorkovanja f_s većom od 2 f_o Hz. Kao i svi veliki teoremi, teorem uzimanja uzoraka je krajnje jednostavan:

(2.2.10)

a zbog njegove važnosti navest ćemo i dokaz.

Dokaz teorema uzimanja uzoraka:

Neka je X(ω)  Fourierova transformacija signala x(t):

(D.1.1)

  (D.1.2)

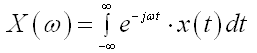
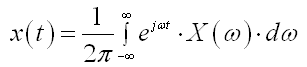Uvedimo periodičnu funkciju

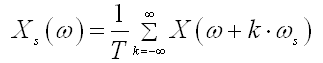  (D.1.3)

Dokaz jednadžbe (2.2.9) temelji se na tome da se uzorak x(kT) može smatrati koeficijentom Fourierovog reda periodične funkcije X_S(ω) .

Razvoj X_S(ω)  u Fourierov red daje:

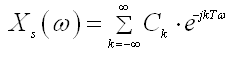  (D.1.4)

gdje su koeficijenti definirani jednadžbom :

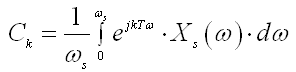  (D.1.5)

Iz definicije Fourierovih koeficijenata definiranih sa (D.1.2), (D.1.3) direktno slijedi:

  (D.1.6)

što znači da uzorkovani signal {x(kT), k = ..., -1, 0, 1, ...}  jednoznačno određuje funkciju X_S(ω  ) . Prema teoremu funkcija X(ω )   je jednaka nuli izvan intervala (-ω_o, ω_o) . Ukoliko je ω_S >2ω_o iz (D.1.3) slijedi

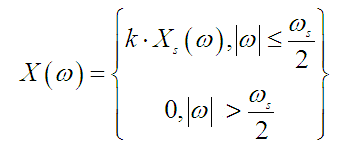  (D.1.7)

Fourierova transformacija kontinuiranog signala je prema iznesenome jedinstveno određena sa X_S(ω ), koji je s druge strane u potpunosti određen uzorkovanim signalom {x(kT), k = ..., -1, 0, 1, ...}. Na taj je način prvi dio teorema dokazan.


Drugi dio, jednadžba (2.2.9), dokazuje se iz jednadžbe (D.1.2) uvrštavanjem X_S(ω ), uz promjenu granica integracije:

 

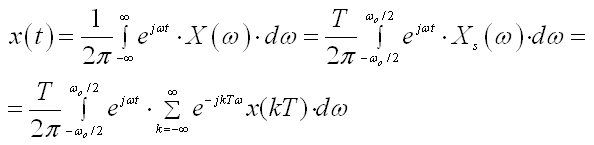(D.1.8)

Zadnja jednadžba slijedi iz (D.1.4) i (D.1.6). Promjenom granica integracije i sumacije dobijemo

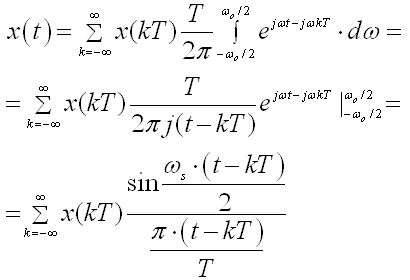    (D.1.9)

kako je ω_S T = 2p  iz (D.1.9) direktno slijedi jednadžba (2.2.9).

Napomena: Primijetili smo da postoji određena neusklađenost u definiranju Nyquistove frekvencije (eng. Nyquist Frequency). Po većini autora  Nyquistova se frekvencija definira na način kako smo je mi definirali kao polovica frekvencije uzorkovanja. Vezano s teorijom uzorkovanja Nyquistova frekvencija predstavlja maksimalnu frekvenciju koju signal može imati da bi se mogao uzorkovati danom frekvencijom uzorkovanja. Za primjere  pogledati Wikipediu (http://en.wikipedia.org/wiki/Nyquist_frequency) ili Web prikaz o Nyquistu (http://www.geocities.com/bioelectrochemistry/nyquist.htm). S druge strane, posebno u teoriji komunikacija pod pojmom Nyquistova frekvencija uzima se dvostruka maksimalna frekvencija signala koji se treba uzorkovati. Kao primjer navodimo Web prikaze Wolframovog MathWorlda (http://mathworld.wolfram.com/NyquistFrequency.html), odnosno projekta Connexions (http://cnx.rice.edu/content/m10791/latest/). Pravilan naziv za dvostruku maksimalnu frekvenciju signala koji se uzorkuje je Nyquistova frekvencija uzorkovanja (eng. Nyquist Sampling Rate ili Nyquist Rate) kako smo i napomenuli na početku ovog poglavlja. Znači treba razlikovati Nyquistovu frekvenciju i Nyquistovu frekvenciju uzorkovanja.

:. Sljedeća stranica > Ilustracija teorema uzoraka frekvencijskim spektrima uzorkovanog signala