Vođeni sustav aproksimiramo prijenosnom funkcijom drugog reda s kašnjenjem
Prijenosna funkcija drugog reda s kašnjenjem je model kojim aproksimiramo sustave koji imaju odziv od aperiodičkog do prigušeno oscilatornog. Karakteriziraju je četiri parametra – pojačanje, dvije vremenske konstante sustava i kašnjenje (u ovom ćemo se dijelu ograničiti samo na cjelobrojno kašnjenje L=MT):
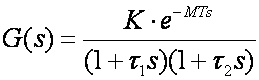(5.2.37)
Ekvivalentna impulsna prijenosna funkcija sustava je
(5.2.38)
a impulsna prijenosna funkcija regulatora
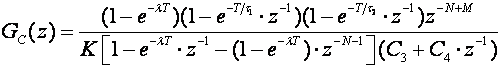(5.2.39)
Uobičajeno je da se željeno kašnjenje NT izjednači sa stvarnim kašnjenjem MT, pa se u brojniku eliminira potencija z-N+M.
Primjer:
Chiu i suradnici (K-C. Chiu, A.B. Corripio, C.L. Smith, Digital Control Algorithms, Part1. Dahlin Algorithm, Inst. & Control Systems, pp. 57-59, Oct. 1973) su u citiranom radu napisali da se isti egzotermički reaktor iz prethodnog primjera može aproksimirati i prijenosnom funkcijom drugog reda:
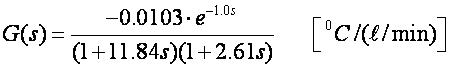
Za λ=0.5 impulsna prijenosna funkcija regulatora je:
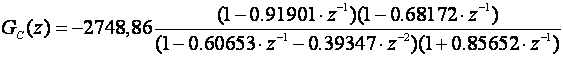
Slika 5.2.23 prikazuje odziv sustava i upravljačku veličinu.
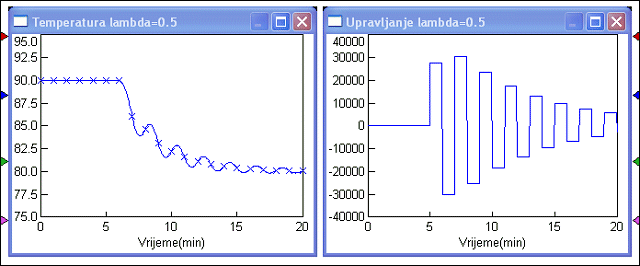
Slika 5.2.23. Odziv sustava uz primjenu Dahlinovog regulatora u slučaju modeliranja sustava prijenosnom funkcijom drugog reda za λ=0.5 (sinteza-Dahlin3.vsm)
Očito je da su treptaji upravljačkog signala još izraženiji, a amplitude upravljačkog signala jako velike, pa je ovaj način vođenja praktički neprimjenjiv. Neprimjenjiv bi vjerojatno bio i zbog toga što zahtijeva jako velike negativne vrijednosti upravljačke varijable - protoka. Prisjetimo se, vrijednosti upravljačke varijable na slici su promjene u odnosu na stacionarno stanje kod kojeg se u reaktoru održava temperatura od 900C. Taj stacionarni protok ovisi o količini topline koju kemijska reakcija u reaktoru oslobađa i sigurno nije 30.000 l/min. Zbog toga zahtjev da se protok smanji za 30.000 l/min je nerealan. Zahtijevao bi negativnu vrijednost protoka, a to fizički nije moguće. Protok vode za hlađenje se može mijenjati samo između nule i neke maksimalne pozitivne vrijednosti.
Dahlin je i za ovaj slučaj predložio ublažavanje treptaja upravljačke veličine zamjenom polova na lijevoj strani realne osi z ravnine konstantama.
Polovi na negativnom dijelu realne z osi eliminiraju se u nazivniku zamjenom varijable z vrijednošću 1, ali se prije toga izluči pol u točki z=1. Za gornji primjer i N=M=1 nazivnik impulsne prijenosne funkcije regulatora glasi:
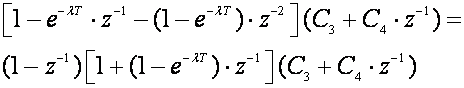(5.2.40)
pa ga zamjenjujemo faktorom
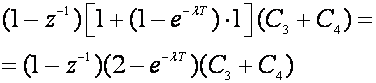(5.2.41)
pa impulsna prijenosna funkcija regulatora glasi:
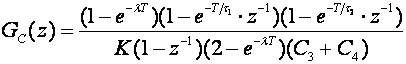(5.2.42)
Za neki
drugi N polinom (N+1)-og reda zamijeni se koeficijentom 
, pa impulsna prijenosna funkcija regulatora uz
pretpostavku N=M glasi:
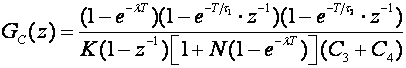(5.2.43)
Primjer:
Pokušajmo eliminirati treptanje upravljačke varijable u gornjem primjeru. Impulsna prijenosna funkcija regulatora glasi:
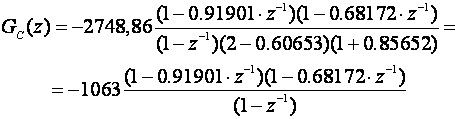
Slika 5.2.24 prikazuje odziv sustava i upravljačku veličinu.
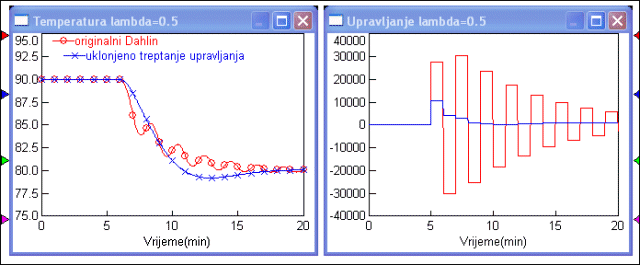
Slika 5.2.24. Rezultati primjene Dahlinovog regulatora kod kojeg je ispravljena pojava treptanja za λ=0.5 (sinteza-Dahlin4.vsm)