Digitalno vođenje on-line (FESB, Split)

Podešavanje parametara PID regulatora postupkom stabilnosne granice

Cilj: Naučiti postupak koji je primjeren eksperimentima u zatvorenoj petlji.

Prvi je postupak primjenjiv za podešavanje parametara regulatora u zatvorenoj petlji kada se petlja povratne veze ne smije prekidati. Zove se postupak stabilnosne granice (eng. Ultimate Cycling). Postupak je krajnje jednostavan. Regulator se prebaci u P mod (T_i se stavi što veći, a T_d jednak nuli). Konstanta pojačanja se lagano diže dok se sustav ne dovede na granicu stabilnosti. Zabilježi se kritična vrijednost pojačanja K_KR i izmjeri perioda neprigušenih oscilacija T_KR. Parametri regulatora se podešavaju prema tablici 5.3.

	K	T_i	T_d
P	0.5 K_KR	-	-
PI	0.45 K_KR	0.833 T_KR	-
PID	0.6 K_KR	0.5 T_KR	0.125 T_KR

Tablica 5.3 Podešavanje parametara kontinuiranog PID regulatora postupkom stabilnosne granice (eng. Ultimate Cycling Method)

Metoda daje zadovoljavajuće rezultate ukoliko se produkt kritičnog pojačanja i statičkog pojačanja samog sustava, koji je bezdimenzionalna veličina, kreće u granicama od 2 do 20. Ako se želi manji prebačaj vrijednosti sve tri konstante treba smanjiti. Na primjer na stranicama US Bureau of Reclamation u popratnim dokumentima programa PIDSim za simulaciju PID vođenja ustava i brana (http://www.usbr.gov/pmts/hydraulics_lab/twahl/pidsim/pidsim.html) daju se sljedeće vrijednosti podešavanja PID regulatora:

PID 1/4 omjera između prvog i sljedećeg prebačaja : K = 0.6 K_KR, T_i = 1.2 T_KR, T = 0.075 T_KR

PID mali prebačaj: K = 0.33 K_KR, T_i = 0.66 T_KR, T = 0.11 T_KR

PID bez prebačaja: K = 0.2 K_KR, T_i = 0.606 T_KR, T = 0.10 T_KR

Ograničenje metode je to što sustav treba biti takav da se može dovesti na granicu stabilnosti. Na primjer sustav sa slike 5.1.9 je drugoga reda prijenosne funkcije 1.68/(.231s²+1.3s+1), pa je strukturno stabilan i ne može se samo povećanjem pojačanja dovesti na rub stabilnosti. Za njega će biti bolja druga metoda podešavanja parametara.

Ilustrirajmo postupak na primjeru sustava koji se može dovesti na rub stabilnosti.

Primjer:

Za sustav prijenosne funkcije 1/s(s+1)(s+2) odredi optimalne parametre podešavanja PID regulatora metodom stabilnosne granice.

Slika 5.1.24 prikazuje trenutak kada smo došli do kritičnog pojačanja.

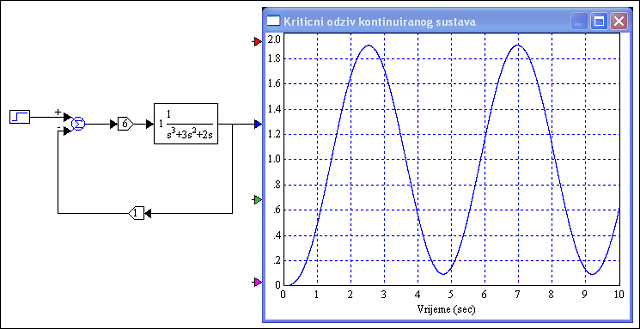
Slika 5.1.24. Uz podešavanje parametara PID regulatora metodom stabilnosne granice (PID-podesavanje_parametara-stab_granica.vsm)

Sa slike smo očitali K_KR =6 i T_KR =4.45 sekundi, pa su prema tome optimalne vrijednosti parametara PID regulatora:

K = 0.6 K_KR = 3.6

T_i = 0.5 T_KR = 2.225

T_d = 0.125 T_KR = 0.55625

Slika 5.1.25 prikazuje odziv sustava vođenog PID regulatorom s ovako podešenim parametrima

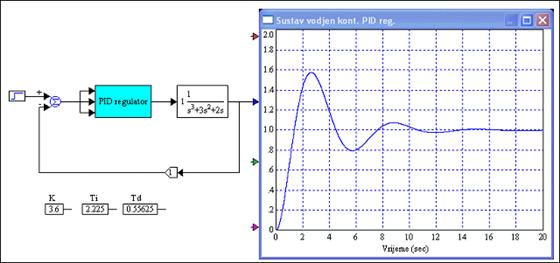
Slika 5.1.25. Sustav vođen kontinuiranim PID regulatorom kojem su parametri određeni metodom stabilnosne granice (PID-podesavanje_parametara-stab_granica.vsm)

Statičko pojačanje sustava je 1, kritično pojačanje 6, pa je ispunjena preporuka o produktu statičkog i kritičnog pojačanja.

Modifikaciju postupka primjenjivu za digitalno vođenje napravio je Y. Takahashi sa suradnicima ( Y. Takahashi CM.J. Rabins, D.M. Auslander, Control and Dynamic Systems, Addison Wesley, 1970) uzevši u obzir i period uzorkovanja. Vrijednosti njegovih parametara za postupak stabilnosne granice dane su u tablici 5.4 (Napomena: Pazite parametri regulatora se navode za idealno paralelnu formu PID regulatora).

	K	K_i =K/T_i	K_d =KT_d
P	0.5 K_KR	-	-
PI	0.45 K_KR– 0.5 K_i	0.54 K_KR T/T_KR	-
PID	0.6 K_KR – 0.5 K_i	1.2 K_KR T /T_KR	0.075 K_KR T /T_KR

Tablica 5.4. Podešavanje parametara diskretnog PID regulatora postupkom stabilnosne granice (eng. Ultimate Cycling Method)

Takahashi napominje i određene korekcije PID parametara ukoliko sustav ima veliko kašnjenje.

Ponovimo prethodni primjer sada za diskretni regulator.

Primjer:

Uz period uzimanja uzoraka T=0.1 (namjerno smo izabrali veći T od preporučenog kako bi se vidjelo da regulator i u tom slučaju radi) parametri diskretnog PID regulatora po Takahashiu trebali bi biti:

K_KR =6

T_KR =4.45

T=0.1

K_i = 1.2 K_KR T /T_KR = 0.1618

K = 0.6 K_KR – 0.5 K_i = 2.0791

K_d = 0.075 K_KR T /T_KR = 0.01011

Prebacimo ove vrijednosti u konstante paralelne realizacije:

K = 2.0791

T_i = K/ K_i = 12.8498

T_d = K_d /K= 0.00486

Slika 5.1.26 prikazuje odzive sustava vođenih diskretnim regulatorom (s obje modifikacije, ali bez zasićenja izvršnog uređaja) za vrijednosti parametara proračunate originalnom Ziegler-Nicholsovom metodom za kontinuirane sustave i Takahshievom metodom i uspoređuje ih s odzivom kontinuiranog regulatora. Upotrijebimo li originalne Ziegler-Nicholsove vrijednosti proračunate za kontinuirane sustave sustav vođen diskretnim regulatorom će biti nestabilan, dok Takahashijeva metoda daje nešto sporiji odziv, a iznos maksimalnog prebačaja ostaje isti kao kod vođenja kontinuiranim PID regulatorom podešenim Ziegler-Nicholsovom metodom.

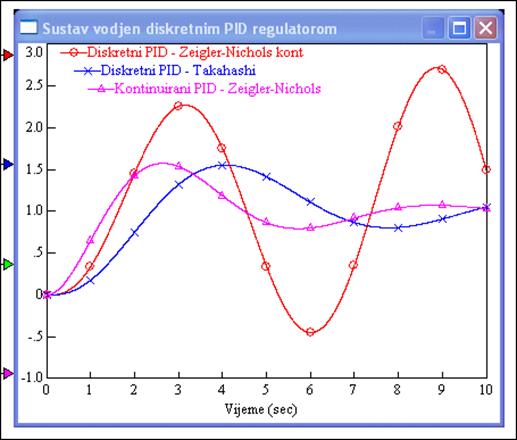
Slika 5.1.26. Usporedba odziva sustava vođenih kontinuiranim i diskretnim regulatorom (s obje modifikacije, ali bez zasićenja izvršnog uređaja) za vrijednosti parametara proračunate metodom stabilnosne granice originalnom Ziegler-Nicholsovom metodom i Takahshievom metodom (PID-podesavanje_parametara-stab_granica_diskretni.vsm)

Drugi se postupak temelji na testiranju sustava otvorene petlje. Snimi se odziv na skokovitu pobudu, te se na temelju njega proračunaju parametri regulatora.