A-4.1.2 Postupak frekvencijskog uzorkovanja
Drugi postupak projektiranja FIR filtra je postupak frekvencijskog uzorkovanja (eng. Frequency Sampling Technique). On se najmanje koristi pa ćemo samo spomenuti zbog cjelovitosti prikaza. Kod ovog se postupka uzorkuje željena frekvencijska karakteristika filtra između frekvencije 0 i frekvencije uzorkovanja fM u N točaka. Ove točke (frekvencije) u z ravnini odgovaraju simetrično raspoređenim točkama na jediničnoj kružnici. Slijedeći je korak primjena diskretne Fourierove transformacije (DFT) na svih N frekvencija i dobivanje N diskretnih uzoraka impulsnog odziva filtra koji ujedno odgovaraju i njegovim koeficijentima.
Za detaljno izučavanje ovog postupka čitaoce upućujemo na literaturu (na primjer Douglas Jones: Frequency Sampling Design Methods for FIR filters )
A-4.1.3 Postupak optimalnog projektiranja (Ramirezov algoritam izmjena)
I na kraju treći postupak koji daje optimalnu strukturu filtra. Poznat je po nazivu Ramirezov algoritam izmjena (eng. Ramez Exchange Algorithm), dok ga neki autori zovu Parks-McClellan algoritam jednake valovitosti (eng. Parks-McClellan equiripple FIR filter design algorithm). Pod pojmom optimalni filtar mislimo da filtar za dani red filtra i grešku aproksimacije ima najoštriji prijelaz iz propusnog u nepropusni dio. Temelji se na Chebyshevljevoj aproksimaciji, a uz minimizaciju valovitosti u području propuštanja filtra. Primjena Ramirezovog algoritma daje FIR filtar koji ima najmanji broj koeficijenata za danu specifikaciju filtra. Algoritam je univerzalni i pomoću njega se može projektirati filtar koji ima više pojasa propuštanja, a u svakom od njih može se definirati drugačiji iznos minimalnog gušenja.
Pogledajmo primjer frekvencijske karakteristike i koeficijenata filtra koji smo također dobili izvrsnim Java appletom za projektiranje FIR filtra metodom Ramirezovog (odnosno Parks-McClellanovog) algoritma. I njega možete koristiti ako kliknete na poveznicu – JAVA applet za projektiranje FIR filtra Ramirezovim algoritmom izmjena . Frekvencije su relativne u odnosu na frekvenciju uzorkovanja, pa se applet može koristiti za projektiranje filtra bilo koje frekvencije uzorkovanja. Mana mu je jedino to što pokriva samo filtre s jednim pojasom propuštanja ili gušenja.
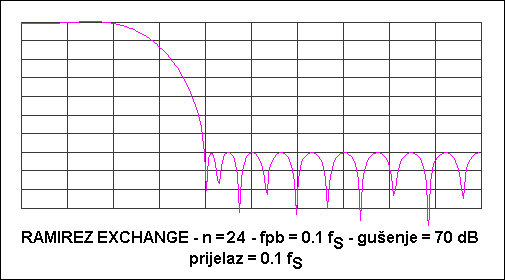
A 4.7 Frekvencijska karakteristika NF filtra proračunatog Ramirezovim algoritmom izmjena. Frekvencijska os je realtivna u odnosu na frekvencijsku uzorkovanja, a slika prikazuje frekvenciji od 0 do Nyquistove frekvencije fN=0.5fS
Filtar projektiran Kaiserovim vremenskim otvorom za gušenje od 60 dB je bio 30-og reda, a Ramirezov (Parc-McClellanov) algoritam daje za gušenje od 70 dB filtar 24-og reda. Koeficijenti filtra su:
Parks-McClellan FIR Filter Design
Filter type: Low pass
Passband: 0 - 0.1
Order: 24
Passband ripple: 1.0 dB
Transition band: 0.1
Stopband attenuation: 70.0 dB
Coefficients:
a[0] = 0.001594903280708857
a[1] = 0.00542881864694688
a[2] = 0.010263362000114701
a[3] = 0.011257781951827653
a[4] = 0.002291467436789652
a[5] = -0.018110657280233314
a[6] = -0.040939123117317344
a[7] = -0.047082650126675646
a[8] = -0.017011961245707072
a[9] = 0.05458750595700548
a[10] = 0.14958796540868
a[11] = 0.23143340947095972
a[12] = 0.26376922128210534
a[13] = 0.23143340947095972
a[14] = 0.14958796540868
a[15] = 0.05458750595700548
a[16] = -0.017011961245707072
a[17] = -0.047082650126675646
a[18] = -0.040939123117317344
a[19] = -0.018110657280233314
a[20] = 0.002291467436789652
a[21] = 0.011257781951827653
a[22] = 0.010263362000114701
a[23] = 0.00542881864694688
a[24] = 0.001594903280708857