2.2.  Kvantizacija signala po vremenu (diskretizacija, uzorkovanje)

U našem okružju postoji veliki broj pojava koje su po svojoj naravi kvantizirane po vremenu. Tipičan je primjer vožnja automobila kod koje vozač ima ulogu regulatora. On sve relevantne veličine na temelju kojih formira upravljačku akciju očitava u diskretnim intervalima vremena. Niti jedan vozač ne gleda kontinuirano i u instrumente i u retrovizore i preko lijevog ramena. On to radi u diskretnim trenucima vremena. Što više, vozač sve te varijable kvantizira i po amplitudi, pa primjerice udaljenost do vozila ispred sebe u svojoj glavi interpretira kao vrlo velika, velika, mala, opasno mala itd, što su u biti kvantizirane vrijednosti varijable "udaljenost" koja je kontinuirana. Situacija je tim složenija što je period diskretizacije po vremenu za svaku varijablu drugačiji.

Drugi primjer su ekonomski sustavi kod kojih se promjene temelje na kalendaru. Iako se ekonomske transakcije odvijaju u svakom trenutku, informacije o važnim ekonomskim pokazateljima na temelju kojih se donose odluke prikupljaju se u diskretnim vremenskim trenucima: dnevno, tjedno, mjesečno, kvartalno, godišnje ...

Treći primjer, nama najzanimljiviji je svakako sustav automatskog vođenja pomoću računala (digitalno vođenje) što je i glavno područje interesa ovog udžbenika. Digitalno vođenje se temelji na algoritmu računala koji je sam po sebi sustav diskretan po vremenu.

Kod digitalnog vođenja u diskretnim vremenskim intervalima događa se sljedeći niz operacija:

begin
- učitaj referentnu veličinu
- učitaj vrijednost procesne veličine
- izračunaj pogrešku kao razliku referentne i procesne veličine
- izračunaj upravljanje
end.

Ovakav se algoritam matematički prikazuje jednadžbom diferencija koje su tipičan način matematičkog prikaza sustava diskretiziranih po vremenu pa ćemo ih u poglavlju 3.1 detaljno izučavati.

Iterativni algoritmi također su primjer sustava diskretnih po vremenu. Kod njih se u određenom diskretnom koraku vrijednost (rješenje) računa na temelju vrijednosti prethodnog koraka. Za primjer uzmimo jednadžbu oblika:

(2.2.1)

(2.2.2)

na primjeru jednadžbe f(x)=3 - (x)^1/2, uz početno rješenje x=0, lako je rješenje pokazati da već u nekoliko koraka konvergira vrijednosti x=1.697.

Kvantizacija po vremenu može se provoditi u identičnim vremenskim intervalima pa govorimo o regularnoj kvantizaciji, a period kvantizacije T nazivamo vrijeme uzorkovanja ili period uzorkovanja. Prikazana je na slici 2.2.1.

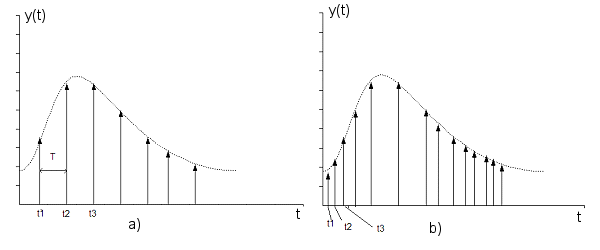
Slika 2.2.1. Način kvantizacije po vremenu a) Regularno kvantiziranje b) Neregularno kvantiziranje

Za regularno kvantizirani signal vrijedi:

(2.2.3)

Slika 2.2.1 b) prikazuje neregularno kvantiziranje za koje vrijedi:

(2.2.4)

Neregularna kvantizacija može biti po nekom zakonu, pa je nazivamo deterministička neregularna kvantizacija. Ukoliko se trenuci uzorkovanja biraju slučajno govorimo o stohastičkoj neregularnoj kvantizaciji.

Iako ponekad neregularna kvantizacija može biti zanimljiva, na primjer period uzorkovanja možemo vezati obrnuto proporcionalno s brzinom porasta veličine koja se kvantizira, što je brzina veća, period je kraći, pa se nagle promjene veličine bolje kvantiziraju, u okviru ovog udžbenika baviti ćemo se isključivo regularnom kvantizacijom. Razlog je taj što se današnjim hardverom lako realiziraju velike brzine uzorkovanja, a analiza sustava s regularno kvantiziranim signalom je puno lakša.

Identično razmišljanje o kvantizaciji se odnosi se i na kvantizaciju po amplitudi.

Digitalno vođenje kao nama najzanimljiviji primjer sustava kvantiziranog po vremenu, najčešće se primjenjuje na kontinuirane sustave što znači da se diskretni signal vođenja treba prije dovođenja na ulaz sustava koji se vodi vratiti natrag u kontinuirani oblik. Kontinuirani signal trebamo rekonstruirati, obnoviti. Zbog toga se postupak diskretizacije po vremenu usko povezuje i s postupkom obnavljanja kontinuirane funkcije (slika 2.2.2).

Teorijski je posebno zanimljivo pitanje neposredne rekonstrukcije disketnog signala. Tražimo odgovor na pitanje :

- U kojim se slučajevima kontinuirani signal može obnoviti tako da bude identičan ulaznom signalu prije diskretizacije? Da li je to uopće moguće?

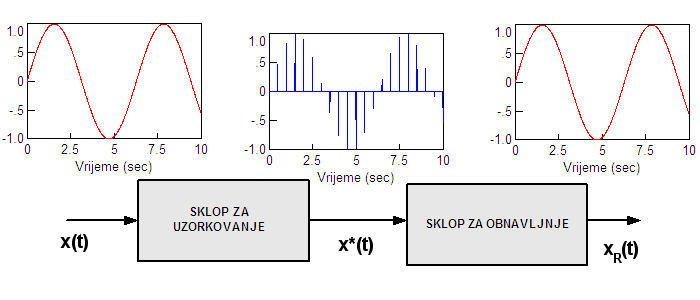
Slika 2.2.2. Uzorkovanje i obnavljanje

Ovim se problemom još 1928.g. bavio H. Nyquist (Nyquist H., Certain Topics in Telegraph Transatssion Theory, AIEE Trans. 47, 617-644, 1928.), a precizno ga je formirao u obliku teorema o uzimanju uzoraka C.A. Shannon 1949.g. ( Shannon, C.E., Communications in Presence of Noise, Proc. IRE, 37, 10-21, 1949.).

:. Sljedeća stranica > Uzorkovanje