4.7.1. Analiza stabilnosti diskretnih sustava opisanih varijablama stanja
U do sada iznesenim definicijama stabilnosti ne mijenja se ništa, samo što je drugačiji zapis. Već u poglavlju 4.1 smo kazali da je sustav asimptotski stabilan ukoliko svi polovi impulsne prijenosne funkcije leže unutar jedinične kružnice.
Neka su jednadžbe varijabli stanja diskretnog sustava dane jednadžbama:
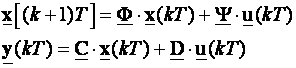(4.7.1)
Prema jednadžbi
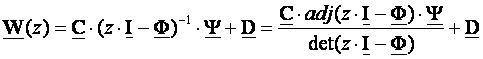(4.7.2)
polovi od W(z)
su jednaki korijenima karakteristične jednadžbe
a oni su opet određeni vlastitim
vrijednostima matrice 
.
Pogledajmo primjer.
Primjer:
Da li je sustav opisan jednadžbama varijabli stanja
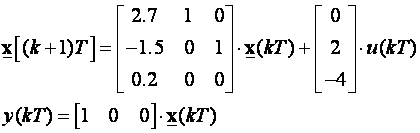
asimptotski stabilan?
Računamo vlastite vrijednosti matrice A:
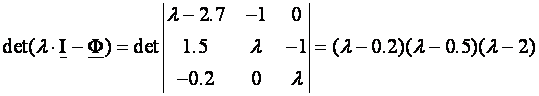
Jedna od vlastitih vrijednosti je izvan jediničnog kruga iz čega slijedi da je sustav asimptotski nestabilan.
Vlastite vrijednosti matrice
ujedno su i korijeni karakteristične jednadžbe i svi polovi
impulsne prijenosne funkcije W(z) (vidi jednadžbu (4.7.2)). Međutim ukoliko
izvedemo cijelu impulsnu prijenosnu funkciju dobiti ćemo
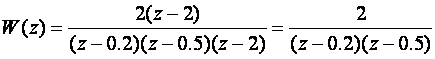
pa bi sustav bio BIBO stabilan zato što je nestabilni pol poništila nula ali ne i asimptotski stabilan s obzirom da taj pol postoji. Sada vidimo važnost naglaska na svi korijeni karakteristične jednadžbe.