4.7.2. Lyapunov teorem stabilnosti
Godine 1892. A.M. Lyapunov, profesor matematike u Harkovu, predložio je dvije metode za određivanje stabilnosti dinamičkih sustava opisanih diferencijalnim jednadžbama. Metoda vrijedi i za linearne i za nelinearne sustave, i za jednoveličinske i za viševeličinske sustave.
Druga metoda poznata pod imenom direktna metoda Lyapunova je pogodnija zato što ne zahtjeva poznavanje karakterističnih vrijednosti sustava. Iako ju je Lyapunov donio za kontinuirane sustave lako se prilagodi i diskretnim sustavima. Ali pogledajmo najprije što je općenito o stabilnosti Lyapunov kazao.
Neka je sustav zadan opisom varijabli stanja općeg oblika
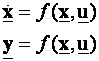 (4.7.3)
(4.7.3)
Za opću analizu stabilnosti bitna je prva jednadžba ali po Lyapunovu potrebno je uključiti i vanjsku pobudu. S druge strane kod definicije asimptotske stabilnosti koja ovisi samo o karakteristikama sustava pobude nema. Zanima nas stabilnost sustava opisanog jednadžbom stanja bez pobude (eng. Unforced State Equation)
![]() (4.7.4)
(4.7.4)
To međutim ne znači da
pobude stvarno nema, samo uključuje zahtjev da pod utjecajem konstantne
pobude u(t)=U sustav dođe u ravnotežno stanje
xr u kojemu nema promjene
![]() , pa možemo to ravnotežno stanje promatrati kao novo
stanje mirovanja oko kojeg analiziramo asimptotsku stabilnost. Drugim
riječima zanima nas da li će se sustav forsirano pomaknut iz tog ravnotežnog
stanja uz nepromijenjenu pobudu opet vratiti u njega.
, pa možemo to ravnotežno stanje promatrati kao novo
stanje mirovanja oko kojeg analiziramo asimptotsku stabilnost. Drugim
riječima zanima nas da li će se sustav forsirano pomaknut iz tog ravnotežnog
stanja uz nepromijenjenu pobudu opet vratiti u njega.
Pogledajmo to na primjeru diskretnih sustava. Krećemo od
![]() (4.7.5)
(4.7.5)
U ravnotežnom stanju i uz konstantnu pobudu vrijedi
![]() (4.7.6)
(4.7.6)
pa je uz pretpostavku
nesingularne matrice ![]() ravnotežno stanje koje zadovoljava
jednadžbu (4.7.6):
ravnotežno stanje koje zadovoljava
jednadžbu (4.7.6):
![]() (4.7.7)
(4.7.7)
Linearni sustavi imaju jedno ravnotežno stanje, a nelinearni ih mogu imati više. Jednadžbu (4.7.5) prebacujemo u oblik bez pobude supstitucijom
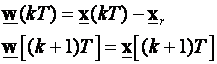 (4.7.8)
(4.7.8)
pa je njen homogeni oblik bez pobude
![]() (4.7.9)
(4.7.9)
Da ne bi pravili zabunu pisanjem u nastavku ćemo umjesto w zadržati stari način označavanja varijabli stanja slovom x. Važno je znati na što se odnosi.
![]() (4.7.10)
(4.7.10)
Važno je znati na što se odnosi, da li smo oko ravnotežnog stanja ili oko 0.
Sustav ostaje u ravnotežnom stanju beskonačno dugo ukoliko se ništa ne mijenja, pobuda se nije mijenjala i nema nikakvih poremećaja. Ukoliko se zbog bilo kojeg razloga pomakne, varijable stanja će se u prostoru stanja kretati po određenoj putanji x(kT). O obliku te putanje ovisi stabilnost ili nestabilnost ravnotežnog stanja, odnosno stabilnost ili nestabilnost diskretnog sustava čiji je to opis varijablama stanja.
Stabilnost u smislu Lyapunova promatra se u prostoru stanja, i to u okolini ravnotežnog stanja kojeg definira simetrično područje P(R). Za bilo koju točku xR =(x1R, x2R ,…, xnR) na rubu tog područja vrijedi
![]() (4.7.11)
(4.7.11)
pa je područje R za sustav drugog reda (n=2) krug, za sustav trećeg reda (n=3) kugla, za sustav četvrtog reda (n=4) hipersfera itd. Izraz na desnoj strani naziva se Euklidska norma.
Definirajmo unutar
hipersfere dvije manja hipersfere radijusa
![]() i
i ![]() , i to tako da vrijedi
, i to tako da vrijedi
![]() . Sada možemo definirati stabilnost u smislu Lyapunova:
. Sada možemo definirati stabilnost u smislu Lyapunova:
Sustav je stabilan
onda i samo onda ukoliko za svaki
![]() postoji
postoji ![]() takav da svaka trajektorija koja je počela iz točke
x0 unutar hipersfere određene radijusom
takav da svaka trajektorija koja je počela iz točke
x0 unutar hipersfere određene radijusom
![]() završi za
završi za ![]() unutar hipersfere određene radijusom
unutar hipersfere određene radijusom
![]() :
:
![]() (4.7.12)
(4.7.12)
Stabilnost po Lyapunovu za sustav drugog reda ilustrira slika 4.7.1.
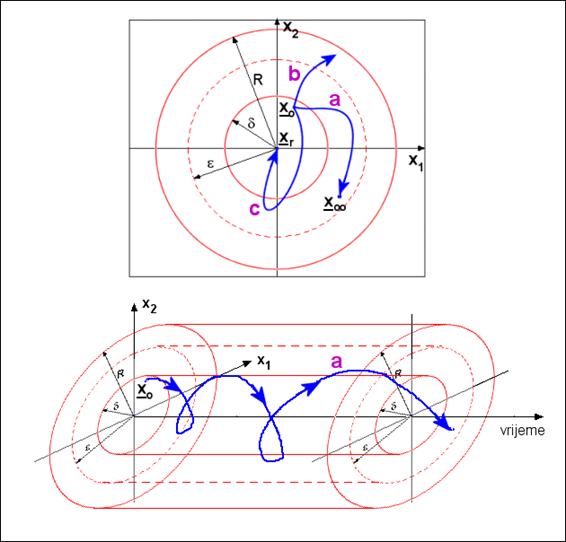
Slika 4.7.1. Ilustracija pojma stabilnosti po Lyapunovu
Sustav je iz ravnotežnog
stanja xR pomaknut u točku x0
unutar područja definiranog radijusom
![]() . Ukoliko on nakon toga cijelo vrijeme ostane unutar
cilindra radijusa
. Ukoliko on nakon toga cijelo vrijeme ostane unutar
cilindra radijusa ![]() možemo kazati da je sustav stabilan. Trajektorija
stabilnog sustava označena je slovom a. Ukoliko se ne može definirati
područje radijusa
možemo kazati da je sustav stabilan. Trajektorija
stabilnog sustava označena je slovom a. Ukoliko se ne može definirati
područje radijusa ![]() sustav je nestabilan (trajektorija b). Slika prikazuje i
treći poseban slučaj asimptotski stabilnog sustava (trajektorija c).
sustav je nestabilan (trajektorija b). Slika prikazuje i
treći poseban slučaj asimptotski stabilnog sustava (trajektorija c).
Sustav je asimptotski
stabilan ukoliko je stabilan i može se izabrati takav
![]() da za ravnotežno stanje xr
da za ravnotežno stanje xr
![]() (4.7.13)
(4.7.13)
Ukoliko bismo htjeli biti u skladu s definicijom asimptotske stabilnosti danom u poglavlju 4.1 ravnotežno bi stanje trebalo biti nula, zato što sustav treba biti bez vanjske pobude.
Ovo je bila opća definicija stabilnosti. Praktično je računamo preko funkcije Lyapunova V(x), koja se za diskretni sustav
![]() (4.7.14)
(4.7.14)
definira tako da zadovoljava tri uvjeta:
1. V(x) je kontinuirana funkcija od x za koju je V(0) = 0.
2. V(x) je pozitivno definitna.
3. ![]() je negativno definitna.
je negativno definitna.
Napomena: Za definicije definitnosti pogledajte Definicije – Neki pojmovi iz matrične algebra.
Funkciju Lyapunova možemo promatrati kao mjeru udaljenosti od ishodišta u prostoru stanja, pa treći uvjet zahtjeva da se u svakom sljedećem trenutku približavamo ishodištu.
Sustav je asimptotski stabilan ukoliko se može pronaći funkcija Lyapunova koja zadovoljava ove uvjete.
Kod linearnih sustava opisanih jednadžbom
![]() (4.7.15)
(4.7.15)
funkcija Lyapunova se definira kao
![]() (4.7.16)
(4.7.16)
Iz trećeg uvjeta dalje slijedi
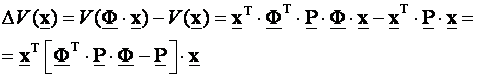 (4.7.17)
(4.7.17)
![]() treba biti negativno definitna što možemo napisati
treba biti negativno definitna što možemo napisati
![]() (4.7.18)
(4.7.18)
gdje je ![]() pozitivno definitna matrica.
pozitivno definitna matrica.
Nužan i dovoljan uvjet da V(x) bude funkcija Lyapunova je da postoji pozitivno definitna matrica P koja zadovoljava jednadžbu
![]() (4.7.19)
(4.7.19)
gdje je Q pozitivno definitna matrica.
Najjednostavnija pozitivno definitna matrica je jedinična matrica I. Pogledajmo primjer:
Primjer:
Provjerimo stabilnost u smislu Lyapunova za diskretni sustav zadan jednadžbama varijabli stanja:
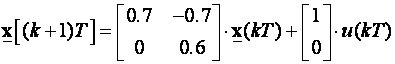
Izaberemo li za matricu Q jediničnu matricu možemo pisati:

iz čega slijede četiri jednadžbe:
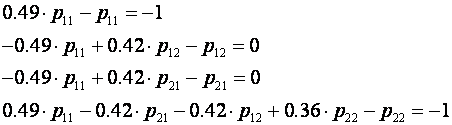
pa je matrica P :
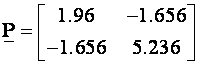
Po Sylvesterovom kriteriju (vidi Definicije – Neki pojmovi iz matrične algebra) slijedi:
![]()
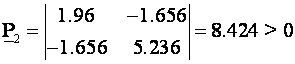
pa je P pozitivno definitna i sustav stabilan.
Slika 4.7.2 prikazuje slobodni odziv sustava za početne
uvjete 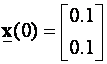 . Period uzorkovanja je T = 0.1.
. Period uzorkovanja je T = 0.1.
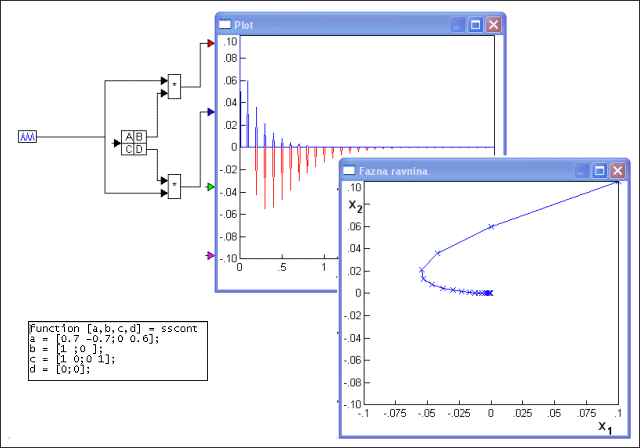
Slika 4.7.2. Slobodni odziv sustava čiju smo stabilnost analizirali Lyapunovim kriterijem (varijable_stanja_stabilnost.vsm)