Filtri s konačnim impulsnim odzivom imaju linearnu faznu karakteristiku i impulsnu prijenosnu funkciju oblika (A 4.1).

   (A 4.1)

Tri su dobro razvijena postupka projektiranja FIR filtra:

a)     Postupak temeljen na Fourierovoj transformaciji i funkciji  vremenskog otvora,

b)    postupak frekvencijskog uzorkovanja, i

c)     postupak optimalnog projektiranja (Ramezov algoritam izmjena).

A 4.1.1 Postupak temeljen na Fourierovoj transformaciji i funkciji  vremenskog otvora

Prvi postupak temeljen na Fourierovoj transformaciji i funkciji vremenskog otvora koji možemo zvati i vremenski prozor s obzirom da se tako i zove u engleskoj literaturi (eng. Window Method)  je direktan i jednostavan. Primijenimo li diskretnu Fourierovu transformaciju (DFT) na funkciju koja predstavlja frekvencijsku karakteristiku željenog filtra dobiti ćemo impulsni odziv željenog filtra. Kako vrijednosti impulsnog odziva FIR filtra odgovaraju slijedu koeficijenata filtra ujedno smo dobili i traženi oblik filtra.

Međutim nije sve tako idealno kako se na prvi pogled čini. Problem je u tome što je ovako dobiveni filtar:

a)     'ne-kauzalan', i

b)    beskonačnog reda.

Filtar je 'ne-kauzalan'  ukoliko se za proračun vrijednosti izlaza u sadašnjem trenutku ne zahtijevaju samo prethodne vrijednosti ulaznog signala x(kT), x[(k-1)T], ... , već i buduće vrijednosti x[(k+1)T], x[(k+2)T], ... Za upotrebu u realnom vremenu to je neizvedivo, pa se filtar prebacuje u kauzalni oblik tako da mu se koeficijenti 'vremenski pomaknu', što drugim riječima znači kašnjenje ulazne sekvence, a s njom i izlaznog signala za određeni, uvijek isti broj diskretnih trenutaka vremena. U većini primjena to i nije toliki problem.

Veći je problem to što bi filtar trebao biti beskonačnog reda, što znači da bi se za proračun izlaza trebao koristiti beskonačni broj diskretnih ulaznih signala. To je naravno praktično neizvedivo. Radi li filtar u realnom vremenu broj članova se treba ograničiti ovisno o tome koliki je period uzorkovanja kako bi se između dva trenutka uzorkovanja mogao izračunati izlaz filtra. Posljedica odsijecanja određenog broja koeficijenata su degradacije filtarskih karakteristika. Očituju se u tome da u području propuštanja filtar više nema ravnu karakteristiku već valovitu (eng. Pass-band Ripplets) , prijelaz između propusnog i ne-propusnog dijela više nije strm već postepen a i u ne-propusnom dijelu se može javiti valovitost (eng. Stop-Band Ripplets) . Slika A 4.1 prikazuje izgled amplitudne frekvencijske karakteristike nisko – propusnog filtra s ucrtanom valovitošću propusnog i nepropusnog dijela.

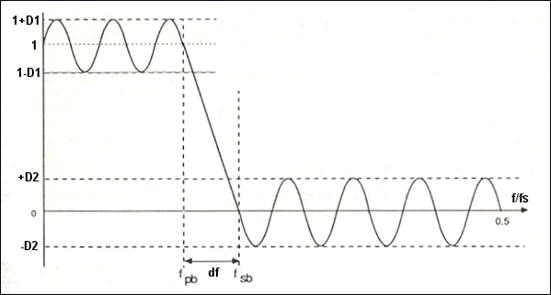
Slika A 4.1 Amplitudna frekvencijska karakteristika nisko – propusnog filtra
(na apscisnoj osi je normirana frekvencija f/f_S  u odnosu na frekvenciju uzorkovanja)

Želimo li ograničiti red filtra ponovo trebamo djelovati na koeficijente. Kod ovog postupka to se radi na način da se sekvenca filtarskih koeficijenata pomnoži s funkcijom vremenskog otvora (prozora) konačne širine. Najjednostavniji je pravokutni vremenski otvor koji odgovara jednostavnom odsijecanju slijeda koeficijenata nakon određenog broja. Pravokutni vremenski otvor daje lošu karakteristiku u nepropusnom dijelu karakteristike, pa se definiraju različite druge funkcije vremenskog otvora koje daju bolju frekvencijsku karakteristiku. Dijelimo ih na fiksne vremenske otvore u kojeg osim pravokutnog spadaju Hanningov, Hammingov i Blackmanov vremenski otvor i promjenjive u koje spada Kaiserov i Dolph-Chebyshev vremenski otvor.  Detaljnu teorijsku analizu i matematički opis vremenskih otvora ovdje izostavljamo i upućujemo zainteresirane na bogatu literaturu. FIR filtre s vremenskim otvorima promatrati ćemo samo kao krajnji korisnici kojima je zadatak projektirati filtar određenih karakteristika.

FIR filtri s fiksnim vremenskim otvorom

 Izgled nekih od fiksnih vremenskih otvora prikazuje Slika A 4.2.

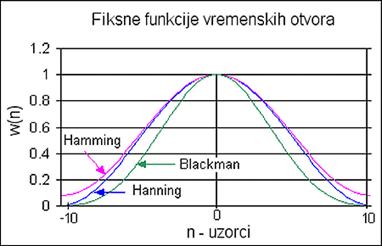
A 4.2 Fiksni vremenski otvori

Izbor prozorske funkcije određuju dva parametra: minimalno gušenje u nepropusnom dijelu frekvencijske karakteristike i širina prijelaznog dijela. Minimalno gušenje se prema oznakama na slici A.4.1 definira u dB kao 20 log D2, a širina prijelaznog dijela je označena sa df. Na Slici A 4.2 dane su vrijednosti minimalnog gušenja i širine prijelaznog dijela karakteristike. Prijelazni dio je ovisan o maksimalnoj frekvenciji sustava f_M (koja treba biti jednaka ili manja od Nyquistove frekvencije) i redu filtra n.

Slika A 4.2 Karakteristike filtarskih prozora

Blackmanov prozor ima najveće gušenje u ne-propusnom dijelu frekvencijske karakteristike, ali mu je zato prijelazni dio za određeni red filtra najveći. To je uvijek tako, jedno dobiješ, ali drugo izgubiš. Treba li nam veliko gušenje, a strma karakteristika, ne ostaje ništa drugo nego povećavati red filtra.

Slika A 4.3. prikazuje izgled amplitudne frekvencijske karakteristike nisko-propusnog FIR filtera 20-og reda gornje granične frekvencije 1000 Hz za različite oblike funkcije vremenskog otvora. Frekvencija uzorkovanja je bila 8000 Hz, a na slici je upisano i gušenje u nepropusnom dijelu i širina prijelaznog dijela karakteristike

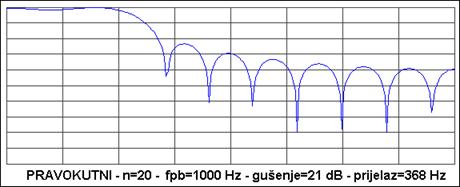
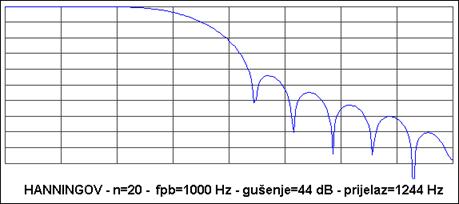
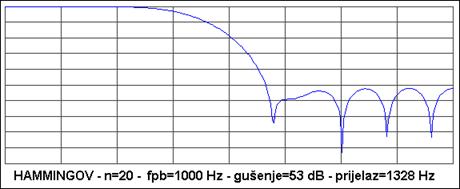
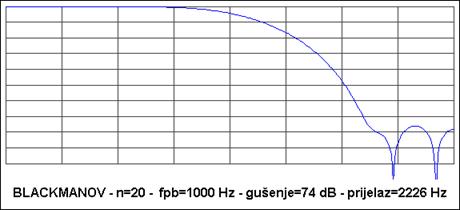
Slika A 4.3. prikazuje amplitudne frekvencijske karakteristiku nisko-propusnog FIR filtera 20-og reda gornje granične frekvencije 1000 Hz za različite oblike funkcije vremenskog otvora za frekvenciju uzorkovanja 8000 Hz. Frekvencija se prikazuje u skokovima od 500 Hz tako da je krajnja frekvencija 4.000 Hz (Nyquistova frekvencija). Gušenje je u skokovima od -10 dB.

Zanimljivo je i usporediti frekvencijsku karakteristiku filtra za različiti red filtra. Slika A 4.4. prikazuje usporedbu za Hammingov vremenski otvor i red filtra n=10, 20 i 30. Što je red manji to je širina prijelaznog dijela veća.

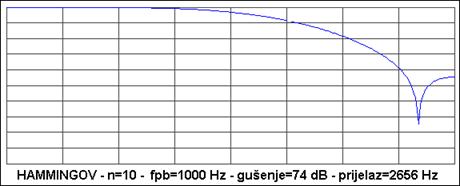
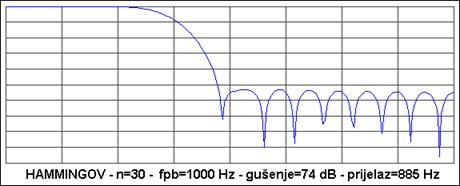
Slika A 4.4. Usporedba FIR filtra s vremenskim prozorom Hammingova tipa za različiti red filtra n = 10 , 20 i 30.

Slike smo dobili izvrsnim Java appletom za projektiranje FIR filtra metodom fiksnog vremenskog okvira, koji i sami možete koristiti ako kliknete na poveznicu – JAVA applet za projektiranje FIR filtra postupkom fiksnog vremenskog otvora  . Applet osim frekvencijske karakteristike daje i koeficijente filtra. Na primjer za Hammingov NP filtar 20-og reda gornje granične frekvencije 1000 HZ koeficijenti  za frekvenciju uzorkovanja 8.000 Hz su:

Hamming window FIR filter

Filter type: LP

Passband: 0 - 1000 Hz

Order: 20

Transition band: 1328 Hz

Stopband attenuation: 53 dB

Coefficients:

a[0] =   0.0012234012

a[1] =   -0.0026044352

a[2] =   -0.0057113464

a[3] =   0.003337278

a[4] =   0.021046996

a[5] =   0.008525811

a[6] =   -0.04710678

a[7] =   -0.060250558

a[8] =   0.072911315

a[9] =   0.299546

a[10] =  0.41485578

a[11] =  0.299546

a[12] =  0.072911315

a[13] =  -0.060250558

a[14] =  -0.04710678

a[15] =  0.008525811

a[16] =  0.021046996

a[17] =  0.003337278

a[18] =  -0.0057113464

a[19] =  -0.0026044352

a[20] =  0.0012234012

Možemo ih koristiti u Vissim-u za simulacije definirajući filtar impulsnom prijenosnom funkcijom oblika (A 4.1) gdje koeficijenti q_i odgovaraju koeficijentima a[i] ili mikroprocesorski implementirati.

FIR filtri s promjenjivim vremenskim otvorom

Filtri promjenjivog vremenskog otvora omogućavaju kontrolu minimalnog gušenja promjenom određenih parametara filtra. Pogledati ćemo primjer Keiserovog filtra. Temelji se na opisu vremenskog otvora Besselovim funkcijama i ima promjenjivi parametar α kojim se određuje oblik krivulje vremenskog otvora. Slika A 4.5  prikazuje oblik Kaiserovog vremenskog otvora za različite vrijednosti parametra α.

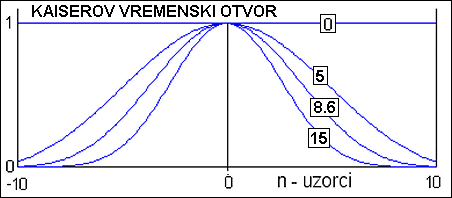
Slika A 4.5. Oblik Kaiserovog vremenskog otvora za različite vrijednosti parametra α

Usporedimo li ovu sliku sa slikom A 4.2 možemo uočiti da se odabirom odgovarajuće vrijednosti parametra α može zamijeniti bilo koji fiksni oblik vremenskog otvora. Na primjer za α = 5 imamo krivulju vrlo sličnu Hammingovoj, a za α = 8.6 Blackmanovoj.

Kaiserov filter se također projektira postavljanjem zahtjeva za iznos minimalnog gušenja u nepropusnom dijelu karakteristike A[dB] i maksimalnom širinom prijelaznog dijela karakteristike. Pri tome se parametar α određuje u ovisnosti o gušenju A izraženom u dB jednadžbama:

α = 0.5842(A - 21)^0·4 + 0·07886(A - 21)  ,  za     21 < A < 50

α  = 0.1102(A – 8.7) ,  za     50 <= A

Pogledajmo primjer. Projektirati ćemo NF filtar gornje granične frekvencije 1.000 Hz koji će imati minimalno gušenje 60 dB , a širinu prijelaznog dijela karakteristike 1000 Hz. Filtar će biti 30 – og reda frekvencijske karakteristike prikazane na gornjem dijelu Slike A 4.6. Želimo li isto gušenje a širinu prijelaznog dijela karakteristike 100 Hz filtar će biti 290-og reda, a frekvencijska karakteristika je prikazana na donjem dijelu Slike A 4.6.

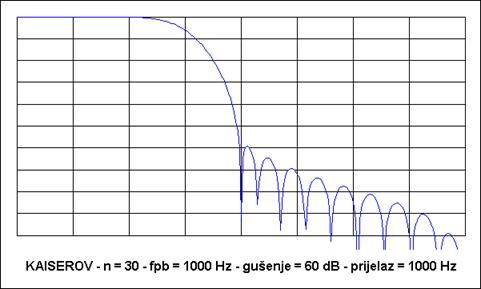
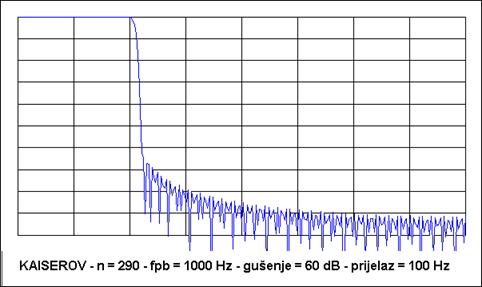
Slika A 4.6 Frekvencijske karakteristike NF filtra FIR tipa s Kaiserovim vremenskim otvorom i različitim karakteristikama. Frekvenciju uzorkovanja je 8000 Hz. Frekvencija se prikazuje u skokovima od 500 Hz tako da je krajnja frekvencija 4.000 Hz (Nyquistova frekvencija). Gušenje je u skokovima od -10 dB.

I ove smo slike dobili izvrsnim Java appletom za projektiranje FIR filtra metodom Kaiserovog vremenskog okvira, koji i sami možete koristiti ako kliknete na poveznicu – JAVA applet za projektiranje FIR filtra postupkom Kaiserovog vremenskog otvora  . Applet osim frekvencijske karakteristike daje i koeficijente filtra. Na primjer za NF filtar 30-og reda gornje granične frekvencije 1000 HZ koeficijenti  za frekvenciju uzorkovanja 8.000 Hz su:

Kaiser Window FIR Filter

Filter type: Low pass

Passband: 0.0 - 1000.0 Hz

Order: 30

Transition band: 1000.0 Hz

Stopband attenuation: 60.0 dB

Coefficients:

a[0] =   -3.992613E-4

a[1] =   -7.619766E-4

a[2] =   8.062371E-4

a[3] =   0.0036405833

a[4] =   0.0022276347

a[5] =   -0.006235567

a[6] =   -0.011866523

a[7] =   -4.335552E-10

a[8] =   0.023303917

a[9] =   0.024477962

a[10] =  -0.018169641

a[11] =  -0.0660483

a[12] =  -0.036572583

a[13] =  0.107386336

a[14] =  0.29041743

a[15] =  0.3745758

a[16] =  0.29041743

a[17] =  0.107386336

a[18] =  -0.036572583

a[19] =  -0.0660483

a[20] =  -0.018169641

a[21] =  0.024477962

a[22] =  0.023303917

a[23] =  -4.335552E-10

a[24] =  -0.011866523

a[25] =  -0.006235567

a[26] =  0.0022276347

a[27] =  0.0036405833

a[28] =  8.062371E-4

a[29] =  -7.619766E-4

a[30] =  -3.992613E-4

.: Slijedeća stranica > Postupak frekvencijskog uzorkovanja i Postupak optimalnog projektiranja